CH NG VƯƠ
M T S BÀI TOÁN T I U TRÊN Đ THỘ Ố Ố Ư Ồ Ị
5.1. Đ TH CÓ TR NG S VÀ BÀI TOÁN Đ NG ĐI NG N NH T.Ồ Ị Ọ Ố ƯỜ Ắ Ấ
5.1.1. M đ u:ở ầ
Trong đ i s ng, chúng ta th ng g p nh ng tình hu ng nh sau: đ đi t đ aờ ố ườ ặ ữ ố ư ể ừ ị
đi m A đ n đ a đi m B trong thành ph , có nhi u đ ng đi, nhi u cách đi; có lúc taể ế ị ể ố ề ườ ề
ch n đ ng đi ng n nh t (theo nghĩa c ly), có lúc l i c n ch n đ ng đi nhanh nh tọ ườ ắ ấ ự ạ ầ ọ ườ ấ
(theo nghĩa th i gian) và có lúc ph i cân nh c đ ch n đ ng đi r ti n nh t (theoờ ả ắ ể ọ ườ ẻ ề ấ
nghĩa chi phí), v.v...
Có th coi s đ c a đ ng đi t A đ n B trong thành ph là m t đ th , v iể ơ ồ ủ ườ ừ ế ố ộ ồ ị ớ
đ nh là các giao l (A và B coi nh giao l ), c nh là đo n đ ng n i hai giao l . Trênỉ ộ ư ộ ạ ạ ườ ố ộ
m i c nh c a đ th này, ta gán m t s d ng, ng v i chi u dài c a đo n đ ng,ỗ ạ ủ ồ ị ộ ố ươ ứ ớ ề ủ ạ ườ
th i gian đi đo n đ ng ho c c c phí v n chuy n trên đo n đ ng đó, ...ờ ạ ườ ặ ướ ậ ể ạ ườ
Đ th có tr ng s là đ th G=(V,E) mà m i c nh (ho c cung) eồ ị ọ ố ồ ị ỗ ạ ặ ∈E đ c gánượ
b i m t s th c m(e), g i là tr ng s c a c nh (ho c cung) e.ở ộ ố ự ọ ọ ố ủ ạ ặ
Trong ph n này, tr ng s c a m i c nh đ c xét là m t s d ng và còn g i làầ ọ ố ủ ỗ ạ ượ ộ ố ươ ọ
chi u dài c a c nh đó. M i đ ng đi t đ nh u đ n đ nh v, có chi u dài là m(u,v),ề ủ ạ ỗ ườ ừ ỉ ế ỉ ề
b ng t ng chi u dài các c nh mà nó đi qua. Kho ng cách d(u,v) gi a hai đ nh u và v làằ ổ ề ạ ả ữ ỉ
chi u dài đ ng đi ng n nh t (theo nghĩa m(u,v) nh nh t) trong các đ ng đi t uề ườ ắ ấ ỏ ấ ườ ừ
đ n v.ế
Có th xem m t đ th G b t kỳ là m t đ th có tr ng s mà m i c nh đ u cóể ộ ồ ị ấ ộ ồ ị ọ ố ọ ạ ề
chi u dài 1. Khi đó, kho ng cách d(u,v) gi a hai đ nh u và v là chi u dài c a đ ng điề ả ữ ỉ ề ủ ườ
t u đ n v ng n nh t, t c là đ ng đi qua ít c nh nh t.ừ ế ắ ấ ứ ườ ạ ấ
5.1.2. Bài toán tìm đ ng đi ng n nh t:ườ ắ ấ
Cho đ n đ th liên thông, có tr ng s G=(V,E). Tìm kho ng cách d(uơ ồ ị ọ ố ả 0,v) t m từ ộ
đ nh uỉ0 cho tr c đ n m t đ nh v b t kỳ c a G và tìm đ ng đi ng n nh t t uướ ế ộ ỉ ấ ủ ườ ắ ấ ừ 0 đ n v.ế
Có m t s thu t toán tìm đ ng đi ng n nh t; đây, ta có thu t toán do E.ộ ố ậ ườ ắ ấ ở ậ
Dijkstra, nhà toán h c ng i Hà Lan, đ xu t năm 1959. Trong phiên b n mà ta s trìnhọ ườ ề ấ ả ẽ
bày, ng i ta gi s đ th là vô h ng, các tr ng s là d ng. Ch c n thay đ i đôiườ ả ử ồ ị ướ ọ ố ươ ỉ ầ ổ
chút là có th gi i đ c bài toán tìm đ ng đi ng n nh t trong đ th có h ng.ể ả ượ ườ ắ ấ ồ ị ướ
Ph ng pháp c a thu t toán Dijkstra là: xác đ nh tu n t đ nh có kho ng cáchươ ủ ậ ị ầ ự ỉ ả
đ n uế0 t nh đ n l n.ừ ỏ ế ớ
Tr c tiên, đ nh có kho ng cách đ n a nh nh t chính là a, v i d(uướ ỉ ả ế ỏ ấ ớ 0,u0)=0. Trong
các đ nh v ỉ≠ u0, tìm đ nh có kho ng cách kỉ ả 1 đ n uế0 là nh nh t. Đ nh này ph i là m tỏ ấ ỉ ả ộ
trong các đ nh k v i uỉ ề ớ 0. Gi s đó là uả ử 1. Ta có:
d(u0,u1) = k1.
67
Trong các đ nh v ỉ≠ u0 và v ≠ u1, tìm đ nh có kho ng cách kỉ ả 2 đ n uế0 là nh nh t. Đ nhỏ ấ ỉ
này ph i là m t trong các đ nh k v i uả ộ ỉ ề ớ 0 ho c v i uặ ớ 1. Gi s đó là uả ử 2. Ta có:
d(u0,u2) = k2.
Ti p t c nh trên, cho đ n bao gi tìm đ c kho ng cách t uế ụ ư ế ờ ượ ả ừ 0 đ n m i đ nh v c a G.ế ọ ỉ ủ
N u V={uế0, u1, ..., un} thì:
0 = d(u0,u0) < d(u0,u1) < d(u0,u2) < ... < d(u0,un).
5.1.3. Thu t toán Dijkstra:ậ
procedure Dijkstra (G=(V,E) là đ n đ th liên thông, có tr ng s v i tr ng s d ng)ơ ồ ị ọ ố ớ ọ ố ươ
{G có các đ nh a=uỉ0, u1, ..., un=z và tr ng s m(uọ ố i,uj), v i m(uới,uj) =
∞ n u (uếi,uj) không là m t c nh trong G}ộ ạ
for i := 1 to n
L(ui) := ∞
L(a) := 0
S := V \ {a}
u := a
while S ≠ ∅
begin
for t t c các đ nh v thu c Sấ ả ỉ ộ
if L(u) +m(u,v) < L(v) then L(v) := L(u)+m(u,v)
u := đ nh thu c S có nhãn L(u) nh nh t ỉ ộ ỏ ấ
{L(u): đ dài đ ng đi ng n nh t t a đ nộ ườ ắ ấ ừ ế
u}
S := S \ {u}
end
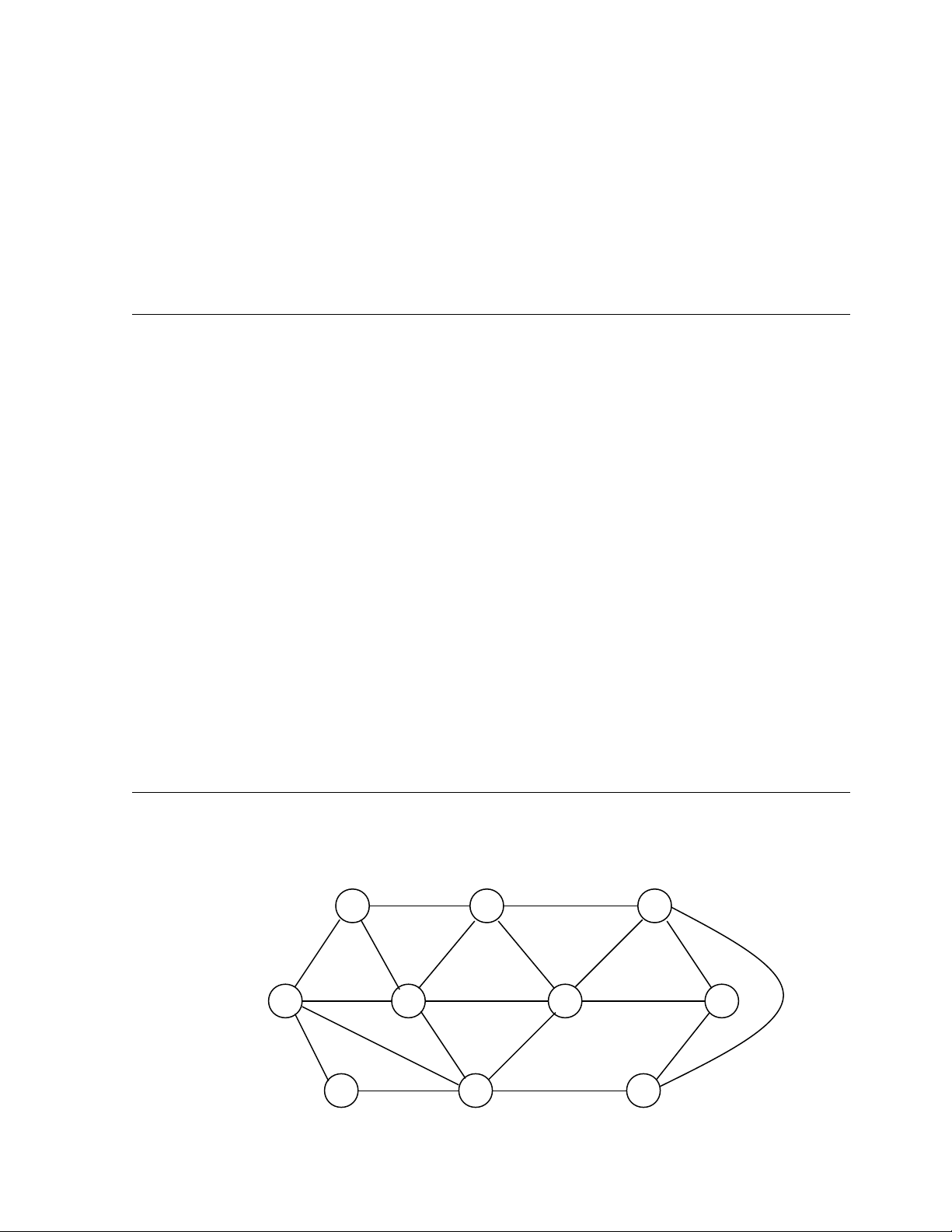
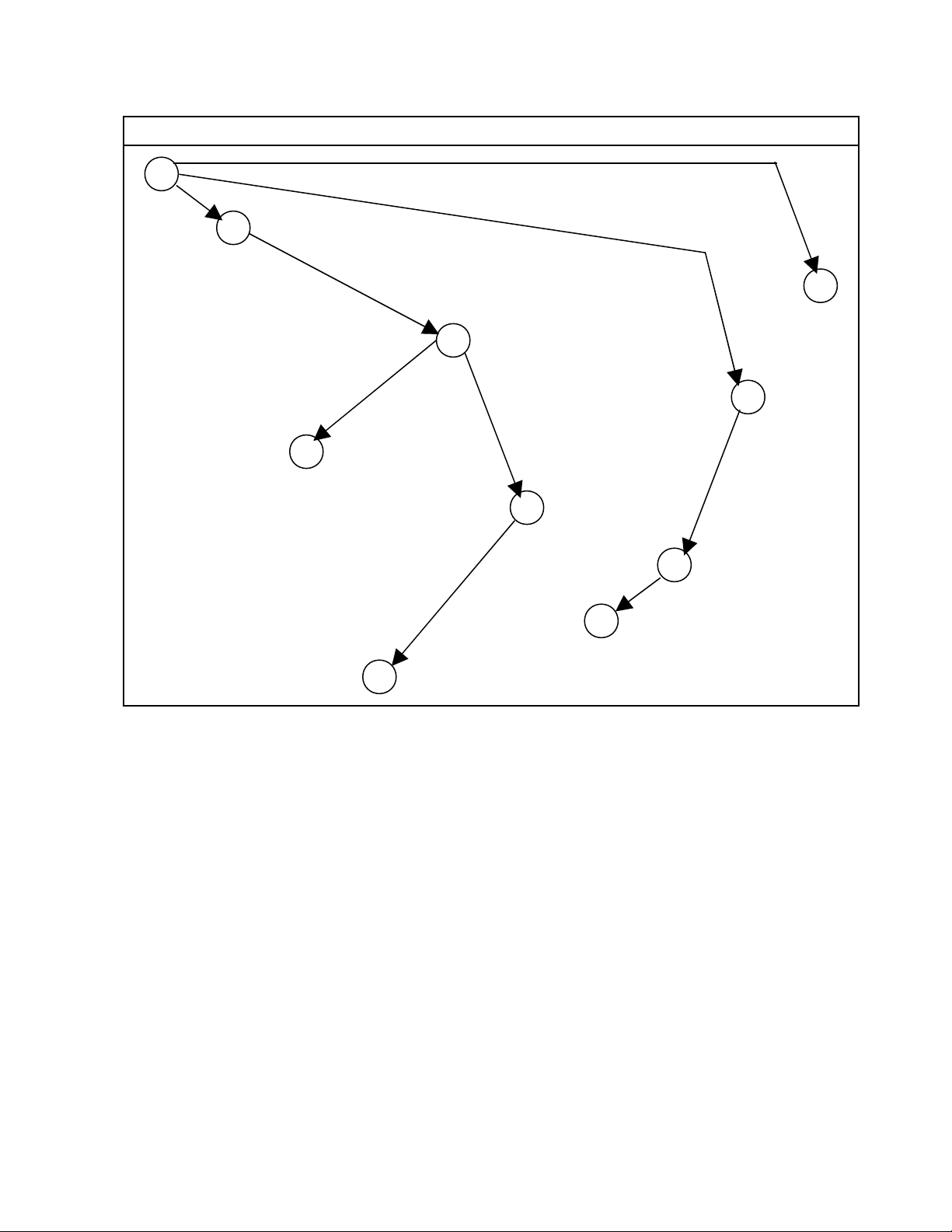
Thí d 1:ụ Tìm kho ng cách d(a,v) t a đ n m i đ nh v và tìm đ ng đi ng n nh t t aả ừ ế ọ ỉ ườ ắ ấ ừ
đ n v cho trong đ th G sau.ế ồ ị
68
a
n
b
e
d
g
m
c
h
k
1
3
3
2
1
4
2
4
2
6
2
3
5
5
6
3
1
2
3
L(a) L(b) L(c) L(d) L(e) L(g) L(h) L(k) L(m) L(n)
5.1.4. Đ nh lý: ịThu t toán Dijkstra tìm đ c đ ng đi ng n nh t t m t đ nh choậ ượ ườ ắ ấ ừ ộ ỉ
tr c đ n m t đ nh tuỳ ý trong đ n đ th vô h ng liên thông có tr ng s .ướ ế ộ ỉ ơ ồ ị ướ ọ ố
Ch ng minh:ứ Đ nh lý đ c ch ng minh b ng quy n p. T i b c k ta có gi thi t quyị ượ ứ ằ ạ ạ ướ ả ế
n p là:ạ
(i) Nhãn c a đ nh v không thu c S là đ dài c a đ ng đi ng n nh t t đ nh a t i đ nhủ ỉ ộ ộ ủ ườ ắ ấ ừ ỉ ớ ỉ
này;
(ii) Nhãn c a đ nh v trong S là đ dài c a đ ng đi ng n nh t t đ nh a t i đ nh này vàủ ỉ ộ ủ ườ ắ ấ ừ ỉ ớ ỉ
đ ng đi này ch ch a các đ nh (ngoài chính đ nh này) không thu c S.ườ ỉ ứ ỉ ỉ ộ
Khi k=0, t c là khi ch a có b c l p nào đ c th c hi n, S=V \ {a}, vì th đứ ư ướ ặ ượ ự ệ ế ộ
dài c a đ ng đi ng n nh t t a t i các đ nh khác a là ủ ườ ắ ấ ừ ớ ỉ ∞ và đ dài c a đ ng đi ng nộ ủ ườ ắ
nh t t a t i chính nó b ng 0 ( đây, chúng ta cho phép đ ng đi không có c nh). Doấ ừ ớ ằ ở ườ ạ
đó b c c s là đúng.ướ ơ ở
Gi s gi thi t quy n p là đúng v i b c k. G i v là đ nh l y ra kh i S b cả ử ả ế ạ ớ ướ ọ ỉ ấ ỏ ở ướ
l p k+1, vì v y v là đ nh thu c S cu i b c k có nhãn nh nh t (n u có nhi u đ nhặ ậ ỉ ộ ở ố ướ ỏ ấ ế ề ỉ
69
0
∞
∞
∞
∞
∞
∞
∞
∞
∞
−
33 2
1
∞
∞
∞
∞
∞
−
−
5 2 2
∞
∞
∞
∞
3
−
−
−
3
25
∞
∞
∞
∞
−
−
−
−
4 6 3
∞
∞
∞
−
−
−
−
−
66
4
∞
∞
−
−
−
−
−
−
10 6
6
∞
−
−
−
−
−
−
−
968
−
−
−
−
−
−
−
7
8
−
−
−
−
−
−
−
−
−
−
8
có nhãn nh nh t thì có th ch n m t đ nh nào đó làm v). T gi thi t quy n p ta th yỏ ấ ể ọ ộ ỉ ừ ả ế ạ ấ
r ng tr c khi vào vòng l p th k+1, các đ nh không thu c S đã đ c gán nhãn b ngằ ướ ặ ứ ỉ ộ ượ ằ
đ dài c a đ ng đi ng n nh t t a. Đ nh v cũng v y ph i đ c gán nhãn b ng đ dàiộ ủ ườ ắ ấ ừ ỉ ậ ả ượ ằ ộ
c a đ ng đi ng n nh t t a. N u đi u này không x y ra thì cu i b c l p th k sủ ườ ắ ấ ừ ế ề ả ở ố ướ ặ ứ ẽ
có đ ng đi v i đ dài nh h n Lườ ớ ộ ỏ ơ k(v) ch a c đ nh thu c S (vì Lứ ả ỉ ộ k(v) là đ dài c aộ ủ
đ ng đi ng n nh t t a t i v ch a ch các đ nh không thu c S sau b c l p th k).ườ ắ ấ ừ ớ ứ ỉ ỉ ộ ướ ặ ứ
G i u là đ nh đ u tiên c a đ ng đi này thu c S. Đó là đ ng đi v i đ dài nh h nọ ỉ ầ ủ ườ ộ ườ ớ ộ ỏ ơ
Lk(v) t a t i u ch a ch các đ nh không thu c S. Đi u này trái v i cách ch n v. Do đóừ ớ ứ ỉ ỉ ộ ề ớ ọ
(i) v n còn đúng cu i b c l p k+1.ẫ ở ố ướ ặ
G i u là đ nh thu c S sau b c k+1. Đ ng đi ng n nh t t a t i u ch a ch cácọ ỉ ộ ướ ườ ắ ấ ừ ớ ứ ỉ
đ nh không thu c S s ho c là ch a v ho c là không. N u nó không ch a v thì theo giỉ ộ ẽ ặ ứ ặ ế ứ ả
thi t quy n p đ dài c a nó là Lế ạ ộ ủ k(v). N u nó ch a v thì nó s t o thành đ ng đi t aế ứ ẽ ạ ườ ừ
t i v v i đ dài có th ng n nh t và ch a ch các đ nh không thu c S khác v, k t thúcớ ớ ộ ể ắ ấ ứ ỉ ỉ ộ ế
b ng c nh t v t i u. Khi đó đ dài c a nó s là Lằ ạ ừ ớ ộ ủ ẽ k(v)+m(v,u). Đi u đó ch ng t (ii) làề ứ ỏ
đúng vì Lk+1(u)=min(Lk(u), Lk(v)+m(v,u)).
5.1.5. M nh đ :ệ ề Thu t toán Dijkstra tìm đ ng đi ng n nh t t m t đ nh cho tr cậ ườ ắ ấ ừ ộ ỉ ướ
đ n m t đ nh tuỳ ý trong đ n đ th vô h ng liên thông có tr ng s có đ ph c t p làế ộ ỉ ơ ồ ị ướ ọ ố ộ ứ ạ
O(n2).
Ch ng minh:ứ Thu t toán dùng không quá nậ−1 b c l p. Trong m i b c l p, dùngướ ặ ỗ ướ ặ
không h n 2(nơ−1) phép c ng và phép so sánh đ s a đ i nhãn c a các đ nh. Ngoài ra,ộ ể ử ổ ủ ỉ
m t đ nh thu c Sộ ỉ ộ k có nhãn nh nh t nh không quá nỏ ấ ờ −1 phép so sánh. Do đó thu t toánậ
có đ ph c t p O(nộ ứ ạ 2).
5.1.6. Thu t toán Floyd:ậ
Cho G=(V,E) là m t đ th có h ng, có tr ng s . Đ tìm đ ng đi ng n nh tộ ồ ị ướ ọ ố ể ườ ắ ấ
gi a m i c p đ nh c a G, ta có th áp d ng thu t toán Dijkstra nhi u l n ho c áp d ngữ ọ ặ ỉ ủ ể ụ ậ ề ầ ặ ụ
thu t toán Floyd đ c trình bày d i đây.ậ ượ ướ
Gi s V={vả ử 1, v2, ..., vn} và có ma tr n tr ng s là W ậ ọ ố ≡ W0. Thu t toán Floydậ
xây d ng dãy các ma tr n vuông c p n là Wự ậ ấ k (0 ≤ k ≤ n) nh sau:ư
procedure Xác đ nh Wịn
for i := 1 to n
for j := 1 to n
W[i,j] := m(vi,vj) {W[i,j] là ph n t dòng i c t j c a ma tr n Wầ ử ộ ủ ậ 0}
for k := 1 to n
if W[i,k] +W[k,j] < W[i,j] then W[i,j] := W[i,k] +W[k,j]
{W[i,j] là ph n t dòng i c t j c a ma tr n Wầ ử ộ ủ ậ k}
70
5.1.7. Đ nh lý:ị Thu t toán Floyd cho ta ma tr n W*=Wậ ậ n là ma tr n kho ng cách nhậ ả ỏ
nh t c a đ th G.ấ ủ ồ ị
Ch ng minh:ứ Ta ch ng minh b ng quy n p theo k m nh đ sau:ứ ằ ạ ệ ề
Wk[i,j] là chi u dài đ ng đi ng n nh t trong nh ng đ ng đi n i đ nh về ườ ắ ấ ữ ườ ố ỉ i v iớ
đ nh vỉj đi qua các đ nh trung gian trong {vỉ1, v2, ..., vk}.
Tr c h t m nh đ hi n nhiên đúng v i k=0.ướ ế ệ ề ể ớ
Gi s m nh đ đúng v i k-1.ả ử ệ ề ớ
Xét Wk[i,j]. Có hai tr ng h p:ườ ợ
1) Trong các đ ng đi chi u dài ng n nh t n i vườ ề ắ ấ ố i v i vớj và đi qua các đ nh trung gianỉ
trong {v1, v2, ..., vk}, có m t đ ng đi ộ ườ γ sao cho vk ∉ γ. Khi đó γ cũng là đ ng đi ng nườ ắ
nh t n i vấ ố i v i vớj đi qua các đ nh trung gian trong {vỉ1, v2, ..., vk-1}, nên theo gi thi t quyả ế
n p,ạ
Wk-1[i,j] = chi u dài ềγ ≤ Wk-1[i,k]+Wk-1[k,j].
Do đó theo đ nh nghĩa c a Wị ủ k thì Wk[i,j]=Wk-1[i,j].
2) M i đ ng đi chi u dài ng n nh t n i vọ ườ ề ắ ấ ố i v i vớj và đi qua các đ nh trung gian trongỉ
{v1, v2, ..., vk}, đ u ch a về ứ k. G i ọγ = vi ... vk ... vj là m t đ ng đi ng n nh t nh th thìộ ườ ắ ấ ư ế
v1 ... vk và vk ... vj cũng là nh ng đ ng đi ng n nh t đi qua các đ nh trung gian trongữ ườ ắ ấ ỉ
{v1, v2, ..., vk-1} và
Wk-1[i,k]+Wk-1[k,j] = chi u dài(về1 ... vk) + chi u dài(vềk ... vj)
= chi u dài ềγ < Wk-1[i,j].
Do đó theo đ nh nghĩa c a Wị ủ k thì ta có:
Wk[i,j] = Wk-1[i,k]+Wk-1[k,j] .
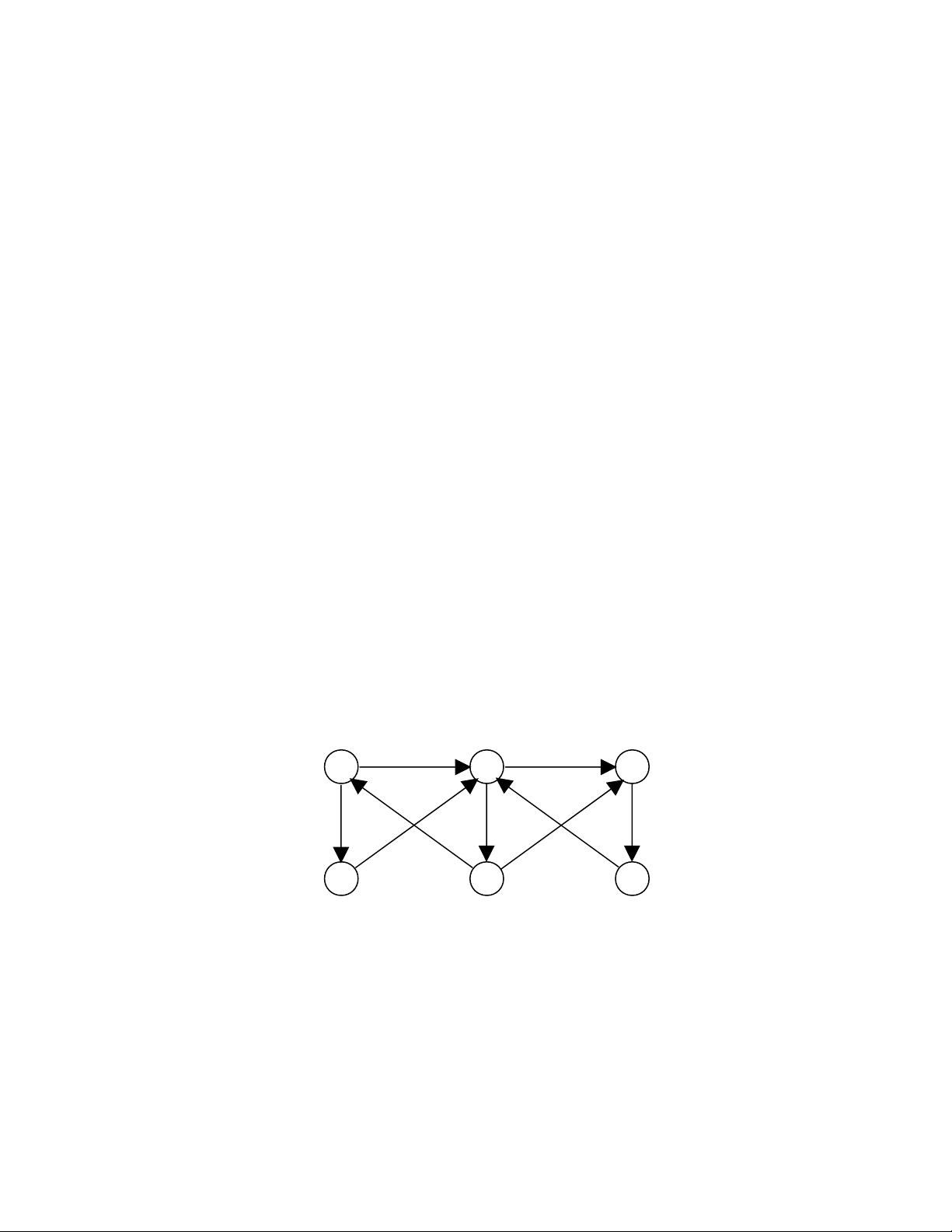
Thí d 2:ụ Xét đ th G sau:ồ ị
Áp d ng thu t toán Floyd, ta tìm đ c (các ô tr ng là ụ ậ ượ ố ∞)
W = W0 =
1
22
4
3
14
27
71
v1
v2
v3
v4
v5
v6
4
7
22
4
1
1
2
3