Chương 3: NHẬN DẠNG MÔ HÌNH KHÔNG THAM SỐ
Huỳnh Thái Hoàng – Bộ môn Điều khiển Tự động
1
Chương 3
NHẬN DẠNG MÔ HÌNH KHÔNG THAM SỐ
Chương 3: NHẬN DẠNG MÔ HÌNH KHÔNG THAM SỐ
3.1. Giới thiệu
3.2. Quá trình ngẫu nhiên
3.2. Phân tích đáp ứng quá độ và phân tích tương quan
3.3. Phân tích đáp ứng tần số
3.4. Phân tích Fourier
3.5. Phân tích phổ
Tham khảo:
[1] L. Ljung (1999), System Identification – Theory for the user.
chương 2 và chương 6.
[2] R. Johansson (1994), System Modeling and Identification.
chương 2 và chương 4.
[3] N. D. Phước và P. X. Minh (2001), Nhận dạng hệ thống điều khiển.
chương 2
3.1 GIỚI THIỆU
3.1.1 Bài toán nhận dạng hệ thống
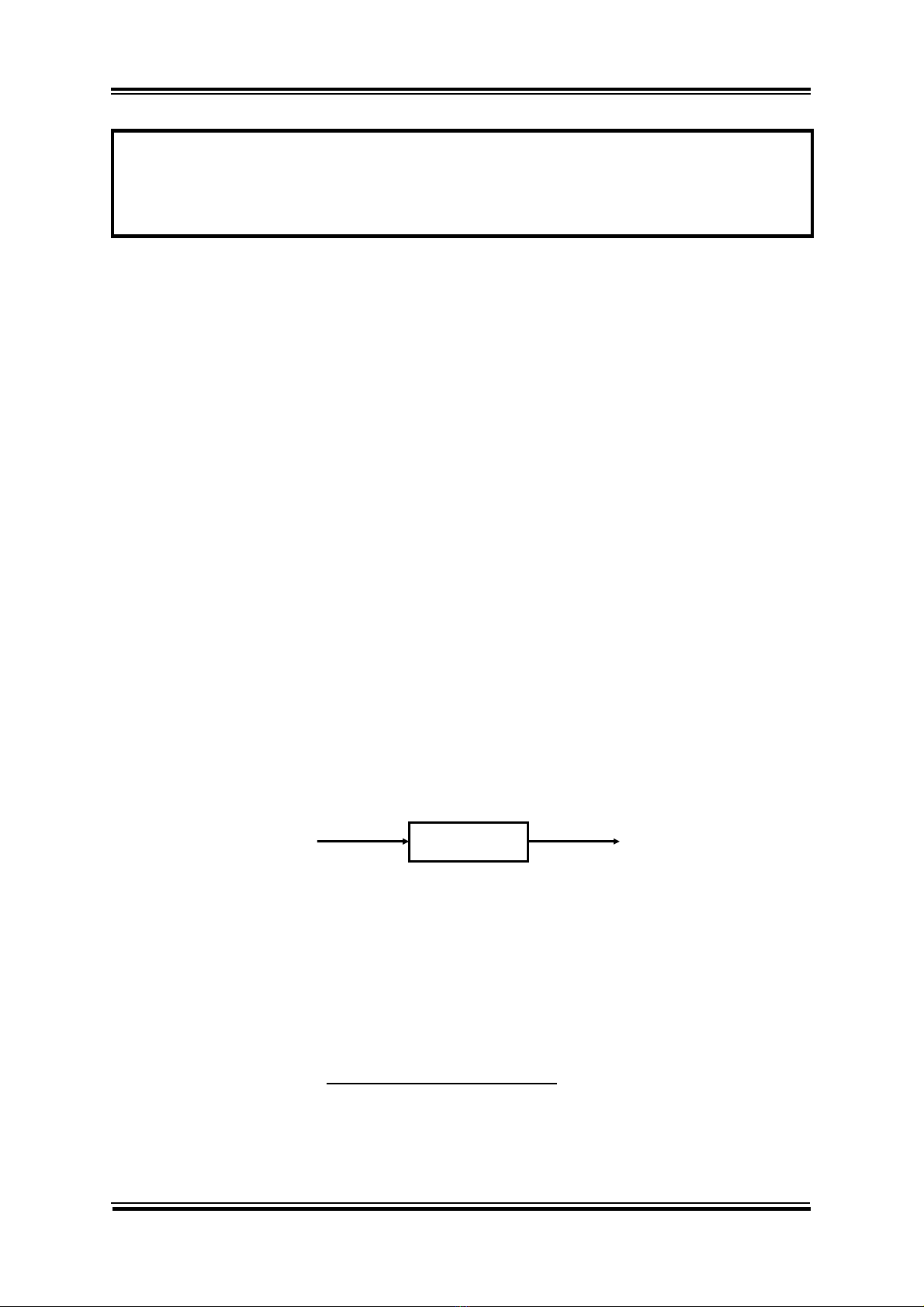
• Nhận dạng hệ thống là xây dựng mô hình toán học của hệ thống dựa trên dữ
liệu vào ra quan sát được.
Hình 3.1: Hệ thống
• Tín hiệu vào và tín hiệu ra của hệ thống tại thời điểm lấy mẫu t tương ứng là
u(t) và y(t). Tùy theo phương pháp nhận dạng mà ta chọn tín hiệu vào thích hợp.
Ký hiệu tập hợp N mẫu dữ liệu quan sát được là:
{}
)(),(,),1(),1( NuNyuyZ NK= (3.1)
• Do dữ liệu thu thập được thông qua quá trình lấy mẫu là dữ liệu rời rạc nên
một cách tự nhiên ta tìm mô hình toán học rời rạc mô tả hệ thống.
• Về mặt toán học, nhận dạng hệ thống là tìm ánh xạ:
)()(: tytuTMa (3.2)
khi biết tập dữ liệu ZN .
Hệ thống
u(t) y(t)
Chương 3: NHẬN DẠNG MÔ HÌNH KHÔNG THAM SỐ
Huỳnh Thái Hoàng – Bộ môn Điều khiển Tự động
2
3.1.2 Hệ thống tuyến tính bất biến
Đáp ứng xung, hàm truyền và đặc tính tần số
• Hệ thống tuyến tính bất biến có thể mô tả bởi hàm truyền.
Hàm truyền của hệ rời rạc là tỉ số giữa biến đổi Z của tín hiệu ra và biến
đổi Z của tín hiệu vào khi điều kiện đầu bằng 0.
)(
)(
)( zU
zY
zG = (3.3)
⇒ )()()( z
U
z
G
z
Y
=
(3.4)
trong đó : ∑
+∞
−∞=
−
=
t
t
ztyzY )()( (3.5)
∑
+∞
−∞=
−
=
t
t
ztuzU )()( (3.6)
• Nếu tín hiệu vào là hàm dirac (U(z)=1) thì tín hiệu ra là:
)()( z
G
z
Y
=
(3.7)
{
}
)()()( 1zGtgty −
==
Z
(3.8)
g(t) gọi là đáp ứng xung của hệ thống.
Đáp ứng xung là đáp ứng của hệ thống khi tín hiệu vào là hàm dirac
• Hệ thống có thể mô tả bởi đáp ứng xung, vì nếu biết tín hiệu vào u(t) bất kỳ ta
có thể xác định được tín hiệu ra dựa vào đáp ứng xung, thật vậy:
(3.4) ⇒ )()()(
t
u
t
g
t
y
∗
=
(3.9)
⇒ ∑
+∞
−∞=
−=
k
ktukgty )()()( (3.10)
Hệ thống nhân quả (causal) có 0)(
=
g
0
<
∀
, do đó:
⇒ ∑
+∞
=
−=
0
)()()(
k
ktukgty (3.11)
• Ký hiệu q là toán tử làm sớm 1 chu kỳ lấy mẫu:
)1()(.
+
=
u
t
uq (3.12)
và q–1 là toán tử làm trể 1 chu kỳ lấy mẫu:
)1()(.
1−=
−tutuq (3.13)
Chương 3: NHẬN DẠNG MÔ HÌNH KHÔNG THAM SỐ
Huỳnh Thái Hoàng – Bộ môn Điều khiển Tự động
3
Biểu thức (3.10) có thể viết lại:
∑
+∞
=
−
=
0
)()()(
k
ktuqkgty (3.14)
hay )()()(
uq
G
y
=
(3.15)
trong đó: qz
k
kzGqkgqG =
+∞
=
−== ∑)()()(
0
(3.16)
• Đặc tính tần số của hệ thống:
ω
ω
j
ez
jzGeG =
=)()( (3.17)
Đặc tính tần số cho biết tỉ lệ về biên độ và độ lệch pha giữa tín hiệu ra ở trạng
thái xác lập và tín hiệu vào hình sin.
Nếu tín hiệu vào là:
tUtu m
ω
sin)(
=
(3.18)
thì ở trạng thái xác lập tín hiệu ra là:
)sin()(
ϕ
ω
+
=
tYty m (3.19)
ta có các quan hệ:
)(
ω
j
m
meG
U
Y= (3.20)
)(
ω
ϕ
j
eG∠= (3.21)
Hệ thống có nhiễu
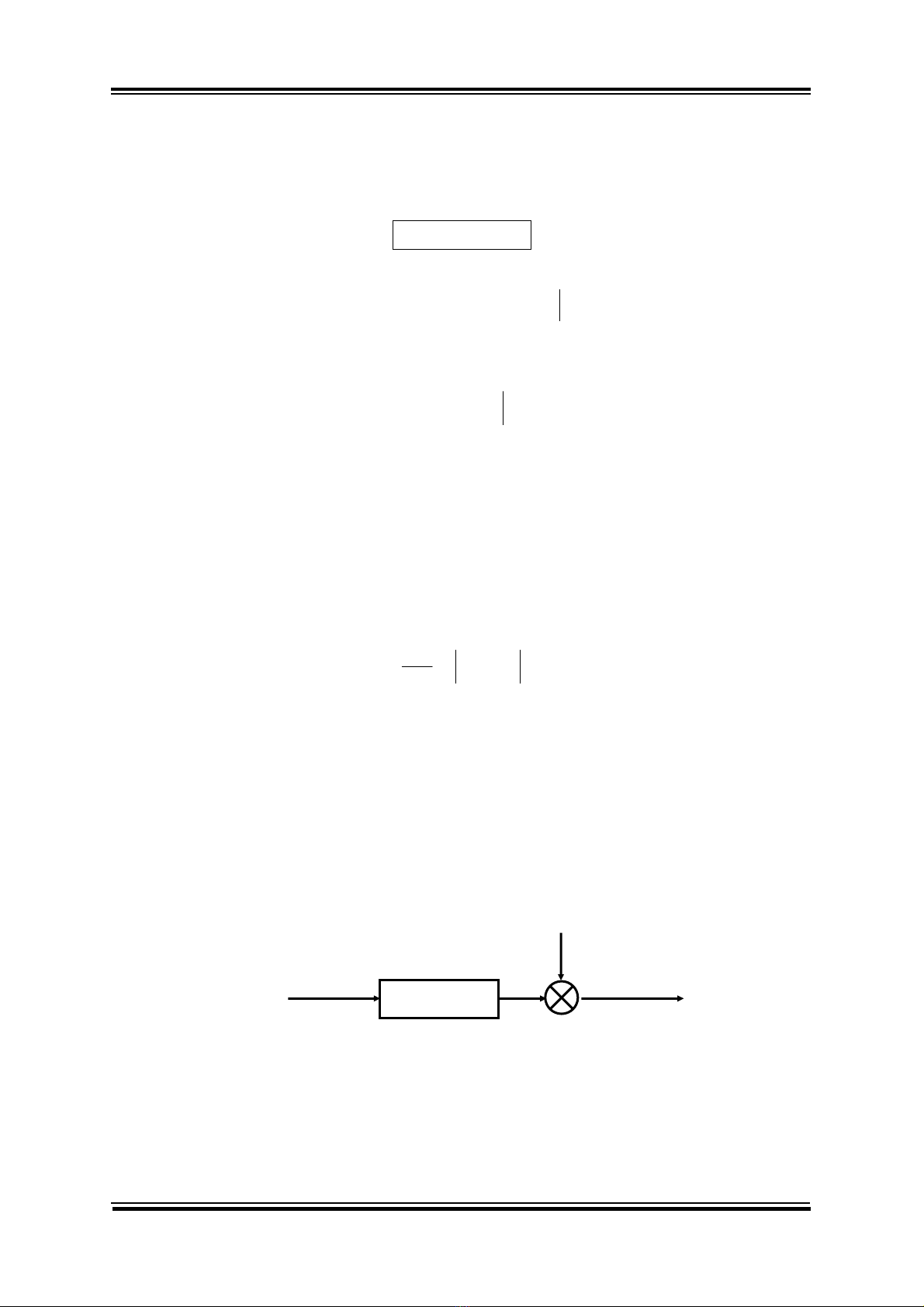
• Mọi hệ thống thực đều bị ảnh hưởng bởi nhiễu (nhiễu đo lường, nhiễu do các
tín hiệu vào không kiểm soát được,…). Giả thiết nhiễu tác động vào hệ thống là
nhiễu cộng. Tín hiệu ra của hệ thống có nhiễu là:
)()()()(
0
tvktukgty
k
+−= ∑
+∞
=
(3.22)
Hình 3.2: Hệ thống có nhiễu
Giả sử nhiễu có thể mô tả bởi:
∑
+∞
=
−=
0
)()()(
k
ktekhtv (3.23)
Hệ thống
u(t) y(t)
v(t)
Chương 3: NHẬN DẠNG MÔ HÌNH KHÔNG THAM SỐ
Huỳnh Thái Hoàng – Bộ môn Điều khiển Tự động
4
trong đó
{}
)(te là nhiễu trắng (nhiễu trắng là chuỗi biến ngẫu nhiên độc lập xác
định bởi một hàm mật độ xác suất nào đó).
Nhận dạng mô hình không tham số
• Phương pháp nhận dạng mô hình không tham số là phương pháp xác định
trực tiếp đáp ứng xung g(t) hoặc đặc tính tần số )(
ω
j
eG của hệ thống (mà
không cần sử dụng giả thiết về cấu trúc mô hình của hệ thống).
• Các phương pháp nhận dạng mô hình không tham số có thể chia làm 2 nhóm:
Phương pháp trong miền thời gian (ước lượng )(
ˆtg ):
* Phương pháp phân tích quá độ (phân tích đáp ứng xung, phân tích
đáp ứng nấc) (xem mục 3.3.1).
* Phương pháp phân tích tương quan (xem mục 3.3.2).
Phương pháp trong miền tần số (ước lượng )(
ˆ
ω
j
eG ):
* Phương pháp phân tích đáp ứng tần số (xem mục 3.4).
* Phương pháp phân tích Fourier (xem mục 3.5).
* Phương pháp phân tích phổ (xem mục 3.6).
3.2 QUÁ TRÌNH NGẪU NHIÊN
Tham khảo: Phụ lục B và D [Johansson, 1994]
3.2.1 Bieán ngaãu nhieân
3.2.1.1 Định nghĩa
• Biến ngẫu nhiên là biến mà giá trị của nó là ngẫu nhiên, không dự đoán trước
được.
• Biến ngẫu nhiên X được gọi là biến ngẫu nhiên liên tục nếu:
i) Tập hợp các giá trị của X có thể lấp đầy một hay một số khoảng của trục số,
thậm chí lấp đầy trục số.
ii) Xác suất để X nhận một giá trị cụ thể nào đó luôn luôn bằng 0, nghĩa là với
mọi số a ta có
{}
0=
=
aXP .
• Hàm mật độ xác suất: Hàm số )(xfXxác định trên toàn bộ trục số được gọi là
hàm mật độ xác suất của biến ngẫu nhiên liên tục X nếu:
i) 0)( ≥xfX với mọi x. (3.24)
ii) 1)( =
∫
+∞
∞−
dxxfX (3.25)
iii) Với mọi a < b:
{}
∫
=<< b
a
XdxxfbXaP )( (3.26)
Chương 3: NHẬN DẠNG MÔ HÌNH KHÔNG THAM SỐ
Huỳnh Thái Hoàng – Bộ môn Điều khiển Tự động
5
TD: Hàm mật độ xác suất của phân bố chuẩn là:
λµ
πλ
2/)( 2
2
1
)( −−
=x
Xexf
3.2.1.2 Kỳ vọng
• Kỳ vọng (Expectation)
Giá trị trung bình, hay kỳ vọng của X, ký hiệu là E(X) được định nghĩa như
sau:
∫
+∞
∞−
== dxxxfX X)()E(
µ
(3.27)
• Tính chất của kỳ vọng:
i) Cho X và Y là hai biến ngẫu nhiên và hai số bất kỳ a và b, giả sử E(X) và
E(Y) tồn tại, thế thì:
)()()(
Y
b
E
Xa
E
b
Y
aX
E
+
=
+
(3.28)
ii) Nếu X là biến ngẫu nhiên liên tục có hàm mật độ phân bố xác suất fX(x) thì:
∫
+∞
∞−
=dxxfxgXgE X)().()]([ (3.29)
(giả thiết ∞<
∫
+∞
∞−
dxxfxg X)(.)( )
iii) Nếu X và Y là hai biến ngẫu nhiên độc lập thì:
)().()(
Y
E
X
E
X
Y
E
=
(3.30)
3.2.1.3 Phương sai
• Phương sai (Variance)
Phương sai của biến ngẫu nhiên X, ký hiệu Var(X) là:
])[()(Var 2
µ
−= XEX (3.31)
trong đó )(X
E
=
µ
.
• Tính chất của phương sai:
i) Nếu X là biến ngẫu nhiên có )(X
E
=
µ
và ∞<)( 2
XE thì:
22 )()(Var
µ
−= XEX (3.32)
ii) Nếu X là biến ngẫu nhiên, a và b là các hằng số thì:
)(Var)(Var 2XabaX =+ (3.33)
iii) Nếu X và Y là hai biến ngẫu nhiên độc lập thì:
)(Va
r
)(Va
r
)(Va
r
Y
X
Y
X
+
=
+
(3.34)