Ôn thi ĐH môn Lý_Quang học

Chia sẻ: Nhan Tai | Ngày: | Loại File: PDF | Số trang:5

Thêm vào BST

Báo xấu

63
lượt xem 7
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Tham khảo tài liệu 'ôn thi đh môn lý_quang học', tài liệu phổ thông, ôn thi đh-cđ phục vụ nhu cầu học tập, nghiên cứu và làm việc hiệu quả

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Ôn thi ĐH môn Lý_Quang học

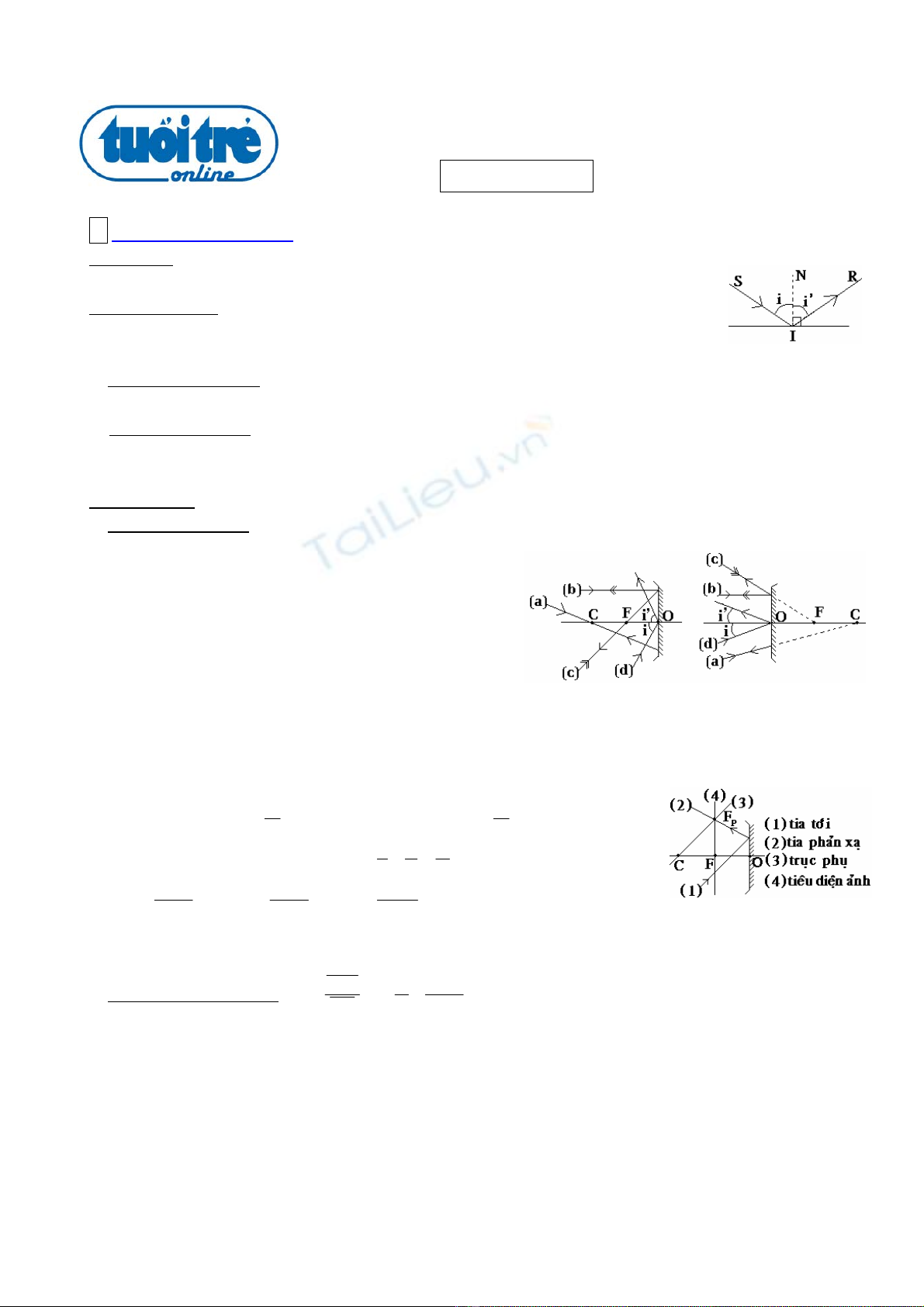
QUANG HOÏC I Söï phaûn xaï aùnh saùng : Ñònh Luaät: Tia phaûn xaï naèm trong maët phaúng tôùi vaø ôû beân kia phaùp tuyeán so tia tôùi. Goùc phaûn xaïbaèng goùc tôùi (i’ = i). 1)Göông phaúng: ♦Vaät vaø aûnh luoân luoân cuøng ñoä lôùn , ñoái xöùng vaø traùi tính chaát vôùi nhau qua göông(vaät thaät qua göông cho aûnh aûo hoaëc vaät aûo qua göông cho aûnh thaät ). ♦ Ñònh lyù göông quay: “ Tia tôùi coá ñònh , khi göông quay moät goùc α quanh moät truïc vuoâng goùc vôùi maët phaúng tôùi ,thì tia phaûn xaï quay moät goùc 2 α cuøng chieàu quay vôùi göông ”. ♦ Nguyeân taéc chung:Tia tôùi qua vaät ( hoaëc coù ñöôøng noái daøi qua vaät) thì cho tia phaûn xaï(hay tia loù) qua aûnh (hoaëc coù ñöôøng noái daøi qua aûnh) ⇔ Vaät laø giao ñieåm cuûa chuøm tia tôùi ; aûnh laø giao ñieåm cuûa chuøm tia phaûn xaï(hay chuøm tia loù) . 2)Göông caàu: ♦ Ñöôøng ñi tia saùng: a) Tia tôùi qua taâm C cuûa göông caàu(hoaëc coù ñöôøng keùo daøi qua taâm) cho tia phaûn xaï truøng tia tôùi. b) Tia tôùi song song truïc chính cuûa göông caàu cho tia phaûn xaï qua tieâu ñieåm chính F (hoaëc coù ñöôøng keùo daøi qua tieâu ñieåm chính F). c) Tia tôùi qua tieâu ñieåm chính F(hoaëc coù ñöôøng keùo daøi qua tieâu ñieåm chính F ) cho tia phaûn xaï song song truïc chính. d) Tia tôùi qua ñænh O cuûa göông caàu , cho tia phaûn xaï ñoái xöùng vôùi tia tôùi qua truïc chính ( i’= i ) e) Neáu tia tôùi baát kyø , thì tia phaûn xaï qua tieâu ñieåm phuï FP(hoaëc coù ñöôøng keùo daøi qua tieâu ñieåm phuï FP). ♦ Göông caàu loõm: f = R > 0 ; Göông caàu loài : f = – R < 0 2 2 ♦ Coâng thöùc xaùc ñònh vò trí vaät aûnh : 1 = 1 + 1 f d d' ⇔ d’= df ⇔ d= d' f ⇔ f= d.d' d−f d' − f d + d' -Vaät thaät (tröôùc göông) : d > 0 ; Vaät aûo(sau göông) : d < 0 -Aûnh thaät (tröôùc göông): d’ > 0 ; Aûnh aûo(sau göông) : d’ < 0 ♦ Ñoä phoùng ñaïi cuûa aûnh : k = A' B' = – d' = − f AB d d−f -Vaät aûnh cuøng chieàu (vaät thaät,aûnh aûo hoaëc vaät aûo, aûnh thaät): k > 0 -Vaät aûnh ngöôïc chieàu(vaät thaät,aûnh thaät hoaëc vaät aûo, aûnh aûo):k < 0 ♦ Vò trí töông ñoái giöõa vaät vaø aûnh qua göông caàu :
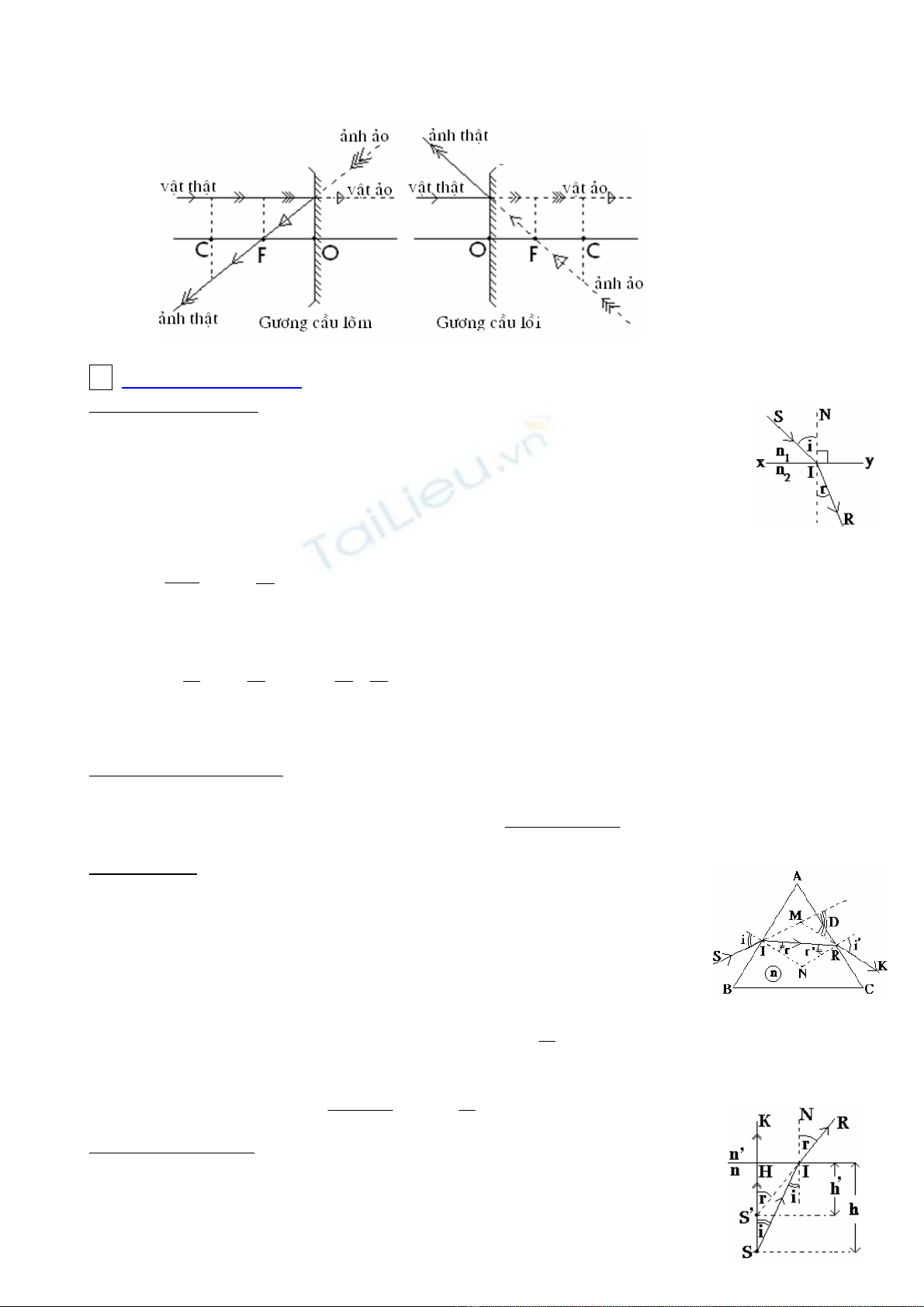
II Söï khuùc xaï aùnh saùng : 1)Phaùt bieåu ñònh luaät: ♦ Tia khuùc xaï(IR) naèm trong maët phaúng tôùi vaø ôû beân kia phaùp tuyeán so vôùi tia tôùi (SI). ♦ Ñoái vôùi moät caëp moâi tröôøng trong suoát nhaát ñònh thì tæ soá giöõa sin goùc tôùi (sini) vaø sin goùc khuùc xaï (sinr) luoân luoân laø moät soá khoâng ñoåi. Soá khoâng ñoåi naøy phuï thuoäc vaøo baûn chaát cuûa hai moâi tröôøng goïi laø chieát suaát tæ ñoái cuûa moâi tröôøng chöùa tia khuùc xaï (moâi tröôøng 2) ñoái vôùi moâi tröôøng chöùa tia tôùi (moâi tröôøng 1), kyù hieäu n21 ⇔ sin i = n21 = n2 = haèng soá ⇔ n1sini = n2sinr sin r n1 vôùi: n1 laø chieát suaát tuyeät ñoái cuûa moâi tröôøng 1 (moâi tröôøng chöùa tia tôùi) n2 laø chieát suaát tuyeät ñoái cuûa moâi tröôøng 2(moâi tröôøng chöùa tia khuùc xaï) n v n1= c ; n2= c ⇒ n21 = 2 = 1 v1 v2 n1 v2 * Trong chaân khoâng hoaëc trong khoâng khí coù chieát suaát (tuyeät ñoái) n = 1 * Trong nhöõng moâi tröôøng khaùc coù chieát suaát (tuyeät ñoái) n > 1 2) Söï phaûn xaï toaøn phaàn: ♦ Tia saùng truyeàn töø moâi tröôøng chieát quang hôn sang moâi tröôøng chieát quang keùm hôn. chieát suaát nhoû ♦ Goùc tôùi lôùn hôn goùc giôùi haïn ( i > igh ) vôùi sinigh =
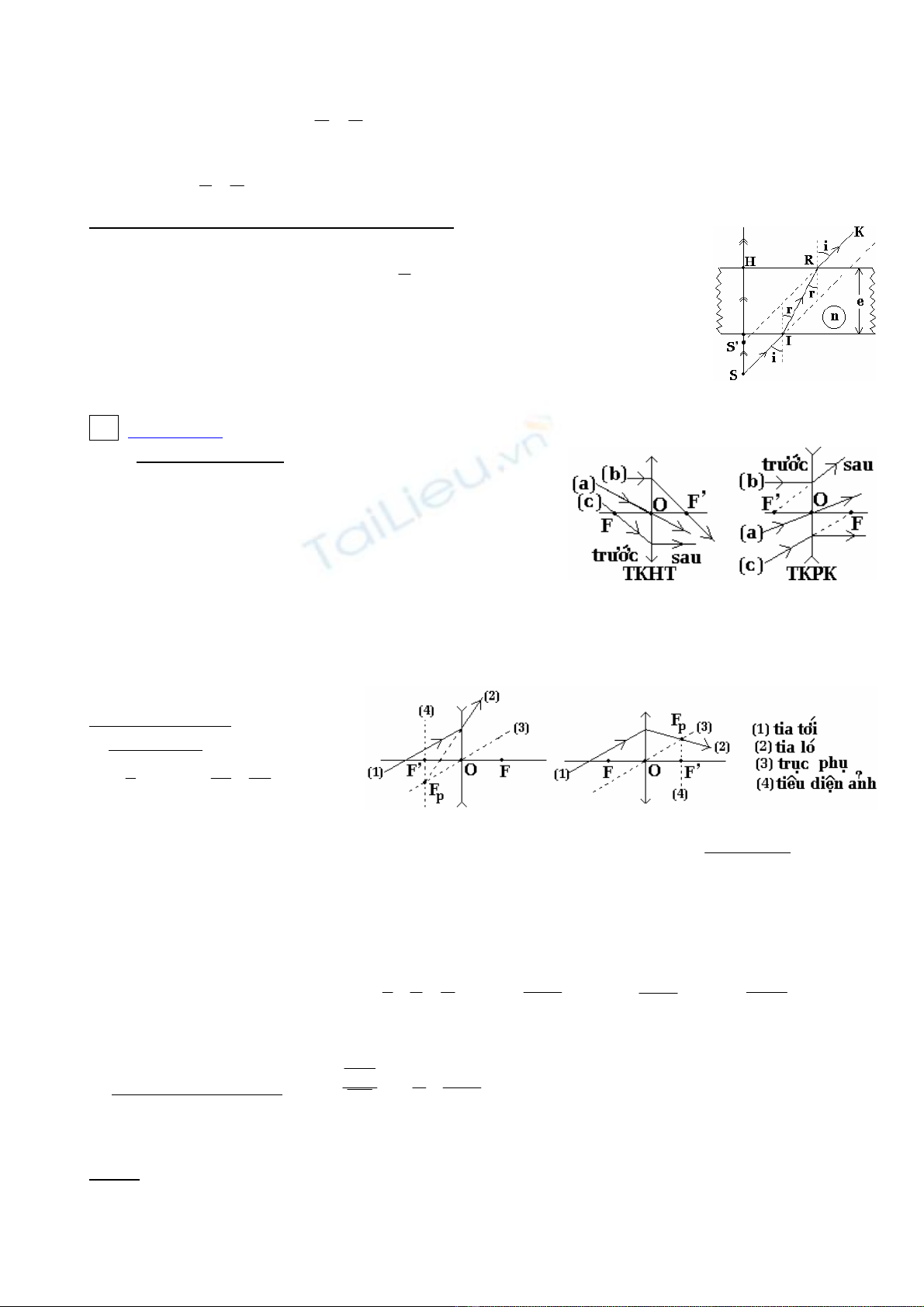
♦ Neáu i , r laø caùc goùc nhoû: h = n (1) h' n' ♦ Qua LCP vaät vaø aûnh luoân luoân cuøng ñoä lôùn , cuøng chieàu , cuøng phía vaø traùi tính chaát vôùi nhau , vì theá töø (1) ⇒ d + d' = O n n' 5) Baûn hai maët song song (baûn maët song song): ♦ sini = nsinr ♦ Neáu i , r laø caùc goùc nhoû: SS’= e(1 – 1 ) n vôùi n laø chieát suaát tæ ñoái cuûa BMSS ñoái vôùi moâi tröôøng beân ngoaøi. ♦ Qua baûn maët song song vaät vaø aûnh luoân luoân cuøng ñoä lôùn , cuøng chieàu vaø traùi tính chaát vôùi nhau (SI // RK) III Thaáu kính : 1) Ñöôøng ñi tia saùng : a/ Tia tôùi qua quang taâm O cuûa thaáu kính cho tia loù truyeàn thaúng . b/ Tia tôùi song song truïc chính cuûa TK cho tia loù qua tieâu ñieåm aûnh chính F’ (hoaëc coù ñöôøng keùo daøi qua tieâu ñieåm aûnh chính F’). c/ Tia tôùi qua tieâu ñieåm vaät chính F (hoaëc coù ñöôøng keùo daøi qua tieâu ñieåm vaät chính F ) cho tia loù song song truïc chính. d/ Neáu tia tôùi baát kyø, thì tia loù qua tieâu ñieåm aûnh phuï FP (hoaëc coù ñöôøng keùo daøi qua tieâu ñieåm aûnh phuï FP). 2) Caùc coâng thöùc : a/ Ñoä tuï(tuï soá): ⎛ ⎞ D = 1 = ( n − 1 )⎜ 1 + 1 ⎟ f ⎝ R1 R2 ⎠ vôùi • D ñôn vò dioáp (Dp) khi f ,R1,R2 coù ñôn vò laø meùt (m). n thaáukính • n laø chieát suaát tæ ñoái cuûa thaáu kính ñoái vôùi moâi tröôøng beân ngoaøi hay: n = n ngoaøi • quy öôùc : * TKHT : f , D > 0 ; TKPK : f , D < 0 * Maët caàu loài : R1 , R2 > 0 * Maët caàu loõm : R1 , R2 < 0 * Maët phaúng : R1 , R 2 = ∞ b/ Coâng thöùc xaùc ñònh vò trí vaät aûnh : 1 = 1 + 1 ⇔ d’= df ⇔ d= d' f ⇔ f= d.d' f d d' d−f d' − f d + d' -Vaät thaät (tröôùc TK) : d > 0 ; Vaät aûo (sau TK) : d 0 ; Aûnh aûo (tröôùc TK) : d’ < 0 c/ Ñoä phoùng ñaïi cuûa aûnh : K = A' B' = – d' = − f AB d d−f -Vaät aûnh cuøng chieàu (vaät thaät,aûnh aûo hoaëc vaät aûo, aûnh thaät): k > 0 -Vaät aûnh ngöôïc chieàu(vaät thaät,aûnh thaät hoaëc vaät aûo, aûnh aûo):k < 0 Löu yù:
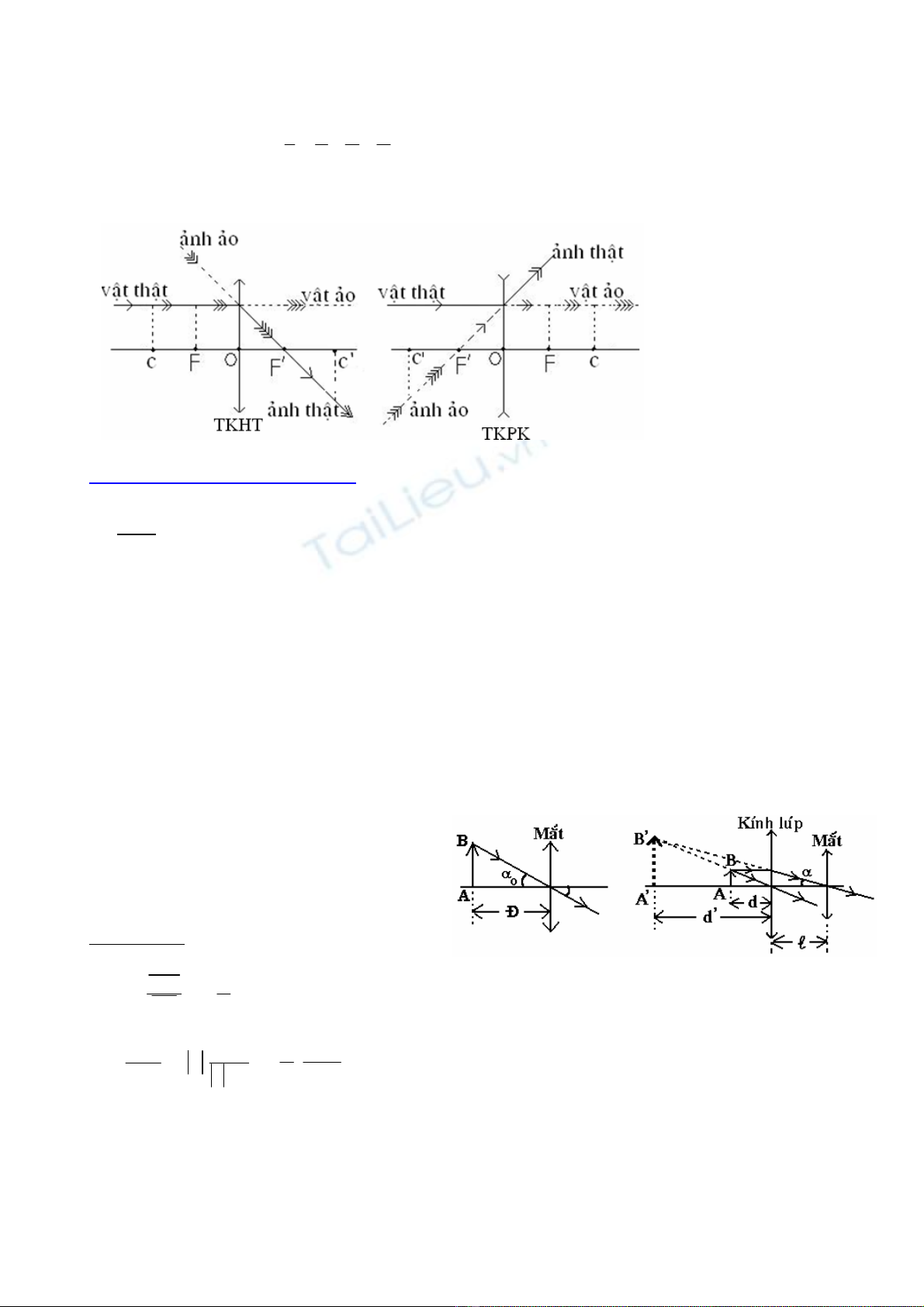
1) Neáu caùc thaáu kính gheùp saùt vôùi nhau thì ñoä tuï hay tieâu cöï töông ñöông cuûa heä laø : D = D1 + D2 + D3 + ... ⇔ 1 = 1 + 1 + 1 + ... f f1 f2 f3 2) Vò trí töông ñoái giöõa vaät vaø aûnh qua thaáu kính : IV. Maét vaø duïng cuï quang hoïc 1) Maét: ♦ Nhìn cöïc vieãn(CV) ⇔ nhìn khoâng ñieàu tieát ⇔ Vaät ôû xa maét nhaát. ♦ Nhìn cöïc caän(CC) ⇔ ñieàu tieát toái ña ⇔ Vaät ôû gaàn maét nhaát. ♦ Khoaûng caùch töø ñieåm cöïc caän ñeán maét khi khoâng mang kính , coøn goïi laø khoaûng cöïc caän : dC = Ñ ♦ Khoaûng caùch töø ñieåm cöïc vieãn ñeán maét khi khoâng mang kính , coøn goïi laø khoaûng cöïc vieãn : dV ♦ Maét khoâng coù taät ( maét bình thöôøng ) : dC ≈ 25cm ; dV = ∞ ♦ Maét caän thò coù ñieåm cöïc caän vaø cöïc vieãn gaàn hôn maét bình thöôøng, ñeå chöûa beänh caän thò phaûi mang thaáu kính phaân kyø coù ñoä tuï thích hôïp sao cho nhìn roõ vaät ôû xa voâ cuøng (d= ∞ ) maø maét khoâng ñieàu tieát , luùc naøy aûnh cuûa vaät hieän leân taïi ñieåm cöïc vieãn cuûa maét . ♦ Maét vieãn thò coù ñieåm cöïc caän xa hôn maét bình thöôøng , ñeå chöûa beänh vieãn thò phaûi mang thaáu kính hoäi tuï coù ñoä tuï thích hôïp sao cho nhìn roõ vaät ôû gaàn nhö maét bình thöôøng maø maét phaûi ñieàu tieát toái ña, luùc naøy aûnh cuûa vaät hieän leân taïi ñieåm cöïc caän cuûa maét . 2) Kính luùp: ♦ Ñoä phoùng ñaïi cuûa aûnh qua kính luùp : K = A' B' = – d' AB d ♦ Ñoä boäi giaùc: tgα G= = K Ñ = − d' . Ñ (coâng thöùc toång quaùt) tgαo d' + l d l − d' vôùi α laø goùc nhìn aûnh cuûa vaät qua kính luùp (hay qua duïng cuï quang hoïc) α o laø goùc nhìn tröïc tieáp vaät AB ( nhìn khoaûng cöïc caän )
• Ngaém chöøng cöïc caän : GC = KC = d' d • Ngaém chöøng voâ cöïc : G∞ = Ñ f • Maét ñaët taïi tieâu ñieåm aûnh cuûa kính luùp: G = Ñ f 3) Kính hieån vi: ♦ Ñoä phoùng ñaïi cuûa aûnh qua kính hieån vi : d' d' K = K1K2 = 1 . 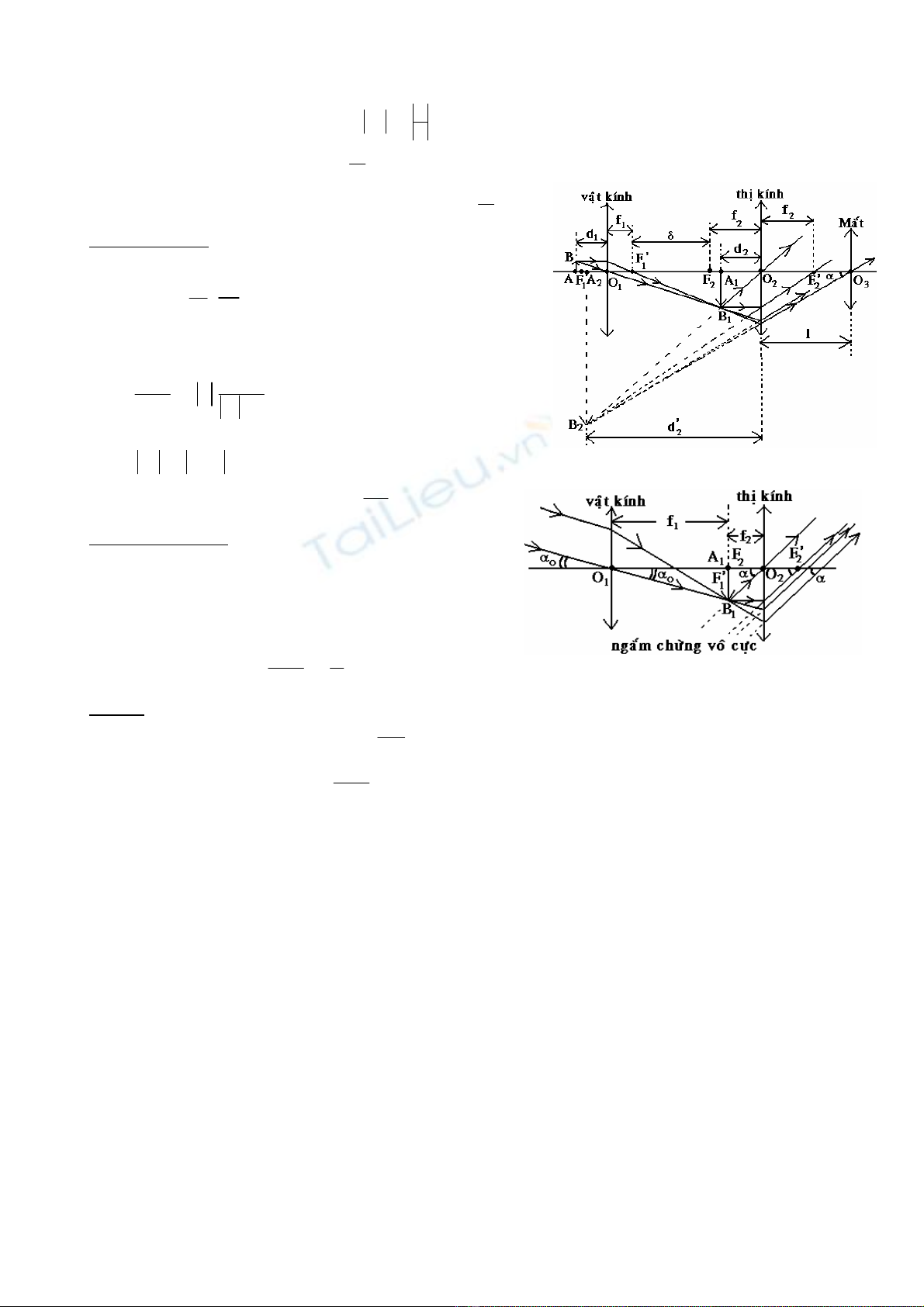2 d1 d2 ♦ Ñoä daøi quang hoïc kính hieån vi : δ = O1O2 – f1 – f2 ♦ Ñoä boäi giaùc: tgα G= = K Ñ (coâng thöùc toång quaùt) tgαo d'2 + l • Ngaém chöøng cöïc caän : GC = KC = K1K2 • Ngaém chöøng voâ cöïc : G∞ = δÑ f1f2 4) Kính thieân vaên: (Duøng ñeå quan saùt vaät ôû xa voâ cuøng) Neáu ngaém chöøng voâ cöïc : ♦ Khoaûng caùch giöõa vaät kính vaø thò kính : O1O2 = f1 + f2 tgα f ♦ Ñoä boäi giaùc: G∞ = = 1 vôùi f1 >> f2 tgαo f2 Löu yù : • Kính luùp vaø kính hieån vi : tg α o = AB Ñ AB • Kính thieân vaên : tg α o = 1 1 f1 GV. Trần Ngọc Lân Trung taâm luyện thi ĐH chất lượng cao Vĩnh Viễn