I. GIỚI THIỆU
ANOVA là kỹ thuật thống kê được sử dụng khi chúng ta muốn so sánh số trung
bình của ≥ 3 nhóm. Kỹ thuật này chia phưong sai của 1 quan sát (observation) thành 2
phần: 1phương sai giữa các nhóm (between groups) và 2phương sai nội nhóm (within
group). Do phưong sai là độ phân tán tương đối của các quan sát so với số trung bình
nên việc phân tích phương sai giúp so sánh các số trung bình dễ dàng (bên cạnh việc
so sánh các phương sai).
Phần này chỉ đề cập đến ANOVA một chiều (one-way ANOVA) theo đó các nhóm
được so sánh dựa trên 1 biến số (yếu tố).
II. NGUYÊN LÝ CỦA ANOVA
Thí dụ minh họa: Thời gian nằm viện của các bệnh nhân đã được tiểu phẫu không có
biến chứng được so sánh với nhau theo ba bác sĩ điều trị (A, B, C). Chọn 1 mẫu ngẫu
nhiên bao gồm 8 bệnh án cho từng bác sĩ, số liệu như sau:
Bảng 1. Thời gian nằm viện của bệnh nhân theo bác sĩ điều trị
PHÂN TÍCH PHƯƠNG SAI
(ANALYSIS OF VARIANCE/ANOVA)
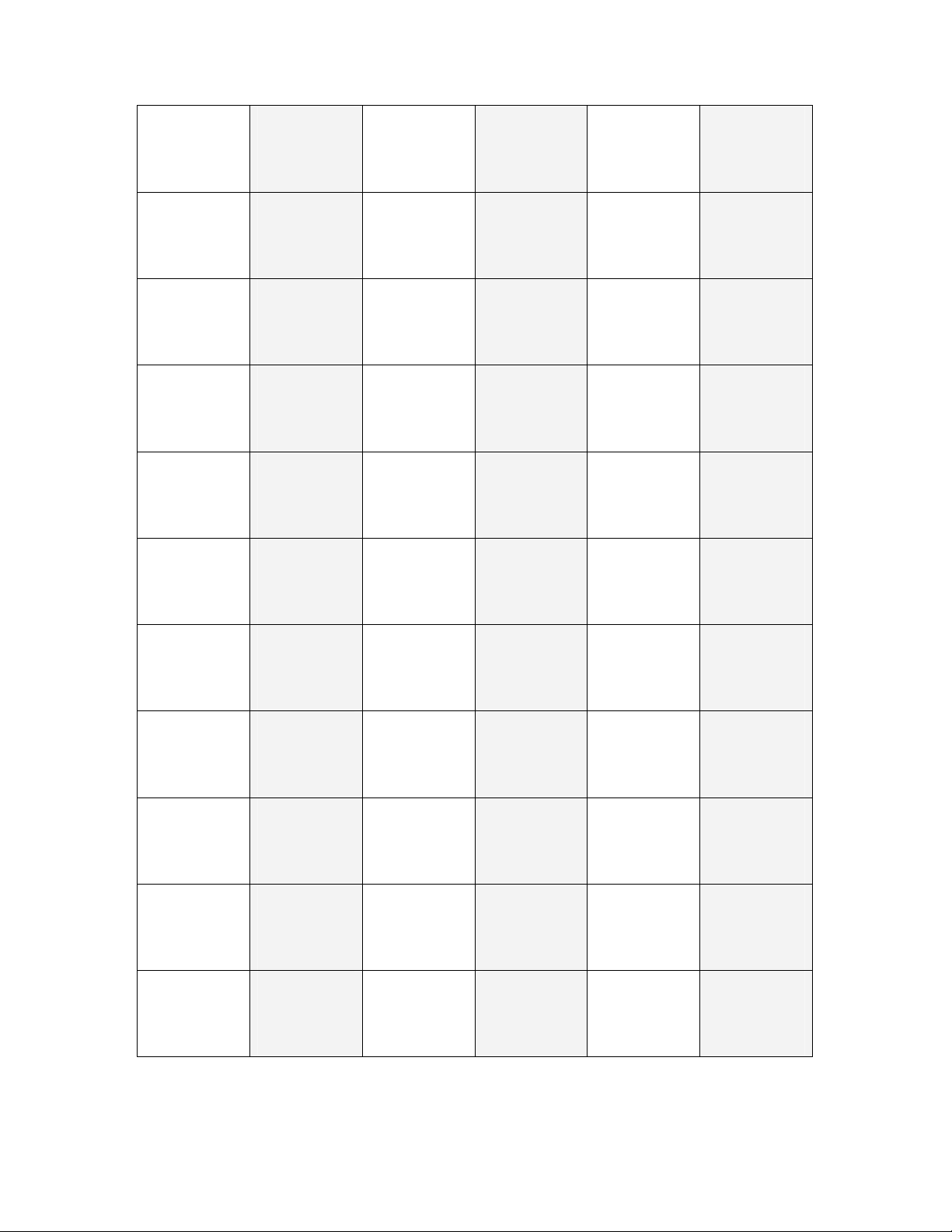
A A2 B B2 C C2
4 16 4 16 5 25
5 25 5 25 3 9
5 25 4 16 3 9
4 16 3 9 3 9
6 36 4 16 3 9
6 36 5 25 3 9
4 16 3 9 4 16
5 25 3 9 5 25
∑A = 39 ∑A2 = 195 ∑B = 31 ∑B2 = 125 ∑C = 29 ∑C2 = 111
4,875
A
3,875
B
3,625
C
4,125
X
Biến số (yếu tố) để so sánh chỉ độc nhất là thời gian nằm viện của bệnh nhân (tính
bằng ngày). Số liệu được phân bố với các ký hiệu như sau:
B/n của BS. A: x1A = 4, x2A = 5, …………………………….., x8A = 5
B/n của BS. B: x1B = 4, x2B = 5, …………………………….., x8B = 3
B/n của BS. C: x1C = 5, x2C = 3, …………………………….., x8C = 5
ij
x
: quan sát thứ i thuộc nhóm j
X
: đại trung bình (số trung bình tính được từ 24 b/n)
, ,
ABC
: số trung bình của các nhóm A, B, và C (tính từ 8 b/n của mỗi nhóm)
Chọn x2A làm mẫu:
(x2A –
) = (5 – 4,125) = 0,875
Hiệu 0,875 có thể được tách ra làm 2:
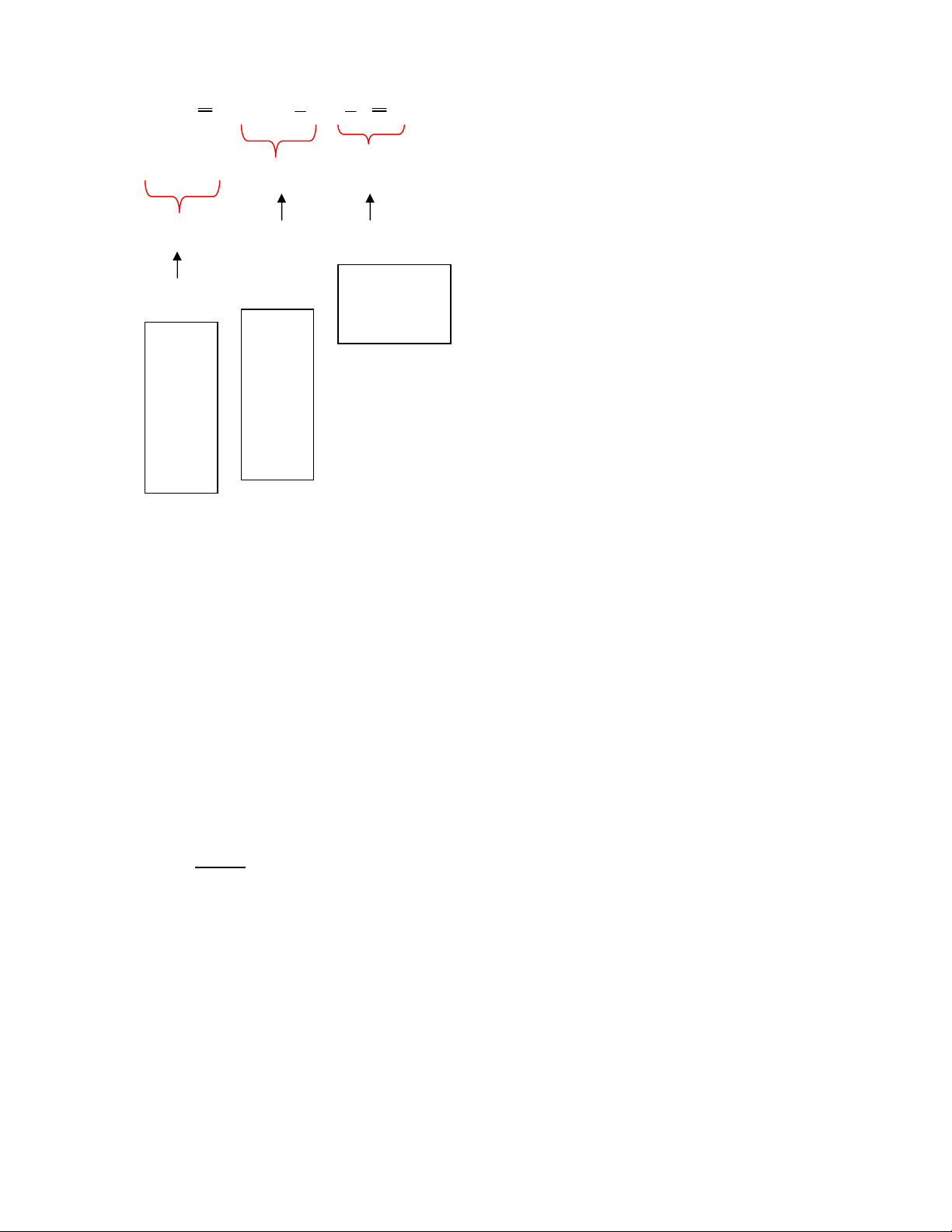
(x2A –
X
) = (x2A –
A
) + (
A X
) = (5 – 4,875) + (4,875 – 4,125)
= (0,125) + (0,750) = 0,875
ANOVA xem xét biến thiên của tất cả các quan sát với số đại trung bình và phân
chúng ra làm 2: biến thiên nội nhóm và biến thiên giữa các nhóm. Nếu số trung bình
của các nhóm khác nhau nhiều thì sự biến thiên giữa chúng và đại trung bình (biến
thiên giữa các nhóm) sẽ đáng kể hơn so với các biến thiên giữa các quan sát trong 1
nhóm với trung bình của nhóm (biến thiên nội nhóm). Nếu số trung bình của các
nhóm không khác nhau nhiều thì biến thiên giữa các nhóm sẽ không lớn hơn so với
biến thiên nội nhóm. Phép kiểm định giả thuyết về 2 phương sai, F test, có thể được sử
dụng để kiểm định tỉ số phương sai giữa các nhóm và phương sai nội nhóm. Giả
thuyết trống của F test cho rằng 2 phương sai này bằng nhau; nếu H0 đúng thì có nghĩa
là biến thiên giữa các nhóm sẽ không lớn hơn so với biến thiên nội nhóm. Trong tình
huống này, không thể kết luận là các trung bình khác lẫn nhau (không có 1 cặp trung
Biến
thiên
giữa 1
quan sát
thuộc
nhóm A
và đại
trung
bình
Biến
thiên
giữa 1
quan sát
thuộc
nhóm A
và trung
bình của
nhóm A
Biến thiên giữa
trung bình của
nhóm A và đại
trung bình
bình nào khác nhau). Ngược lại, nếu từ chối được H0 thì kết luận được là không phải
tất cả các trung bình đều bằng nhau (có ít nhất 1 cặp trung bình khác nhau).
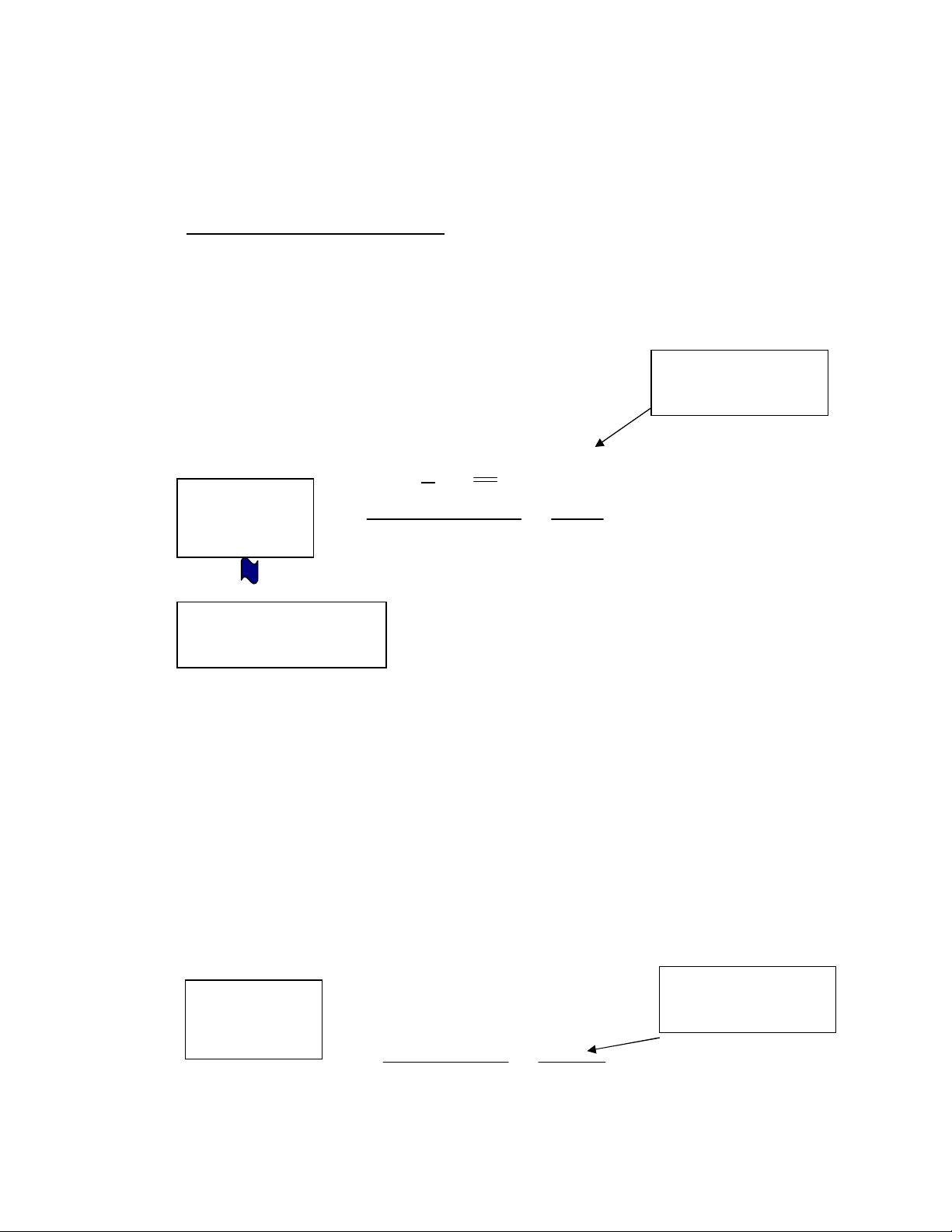
III. CÁCH TÍNH TRONG ANOVA
+ Tính phương sai giữa các số trung bình nhóm so với đại trung bình:
2
( )
1 1
j
j
n x X
SSB
j j
+ Tính phương sai giữa các quan sát trong từng nhóm so với số trung bình của
nhóm:
2
( 1)
( 1)
j j
j
n s
S S W
n N j
Ước lượng
phương sai giữa
các nhóm
Tổng bình phương giữa
các nhóm (Sum of
Squares Between–SSB)
Trung bình bình phương
giữa các nhóm (Mean square
between groups – MSB)
Ước lượng
phương sai nội
nhóm
═
═
T
ổng b
ình ph
ương
n
ội
nhóm (Sum of Squares
Within – SSW)