
BÁO CÁO K T QUẾ Ả
NGHIÊN C U, NG D NG SÁNG KI NỨ Ứ Ụ Ế
1. L i gi i thi uờ ớ ệ
M t bài toán v t lí hay và khó là bài toán ch a đng nhi u hi n t ngộ ậ ứ ự ề ệ ượ
v t lí và ph i s d ng nhi u ki n th c toán h c đ gi i bài toán đó. Trongậ ả ử ụ ề ế ứ ọ ể ả
gi ng d y v t lí, vi c s u t m, biên so n các bài toán v t lí hay và khó làả ạ ậ ệ ư ầ ạ ậ
nhi m v c a ng i giáo viên, đc bi t khi d y các h c sinh khá gi i.ệ ụ ủ ườ ặ ệ ạ ọ ỏ
Toán h c có nhi u ng d ng trong nhi u ngành khoa h c khác nhau trong đóọ ề ứ ụ ề ọ
có V t lí h c. Vi c ng d ng các ki n th c toán h c vào gi i quy t các bàiậ ọ ệ ứ ụ ế ứ ọ ả ế
toán v t lí cũng r t đa d ng và phong phú nh : ng d ng các b t đng th c,ậ ấ ạ ư ứ ụ ấ ẳ ứ
các ph ng trình, h ph ng trình, đo hàm, tích phân, nguyên hàm, hình h cươ ệ ươ ạ ọ
s c p… Đc bi t r t nhi u bài toán v t lí có đi u ki n biên thì không thơ ấ ặ ệ ấ ề ậ ề ệ ể
thi u vi c ng d ng tích phân và nguyên hàm đ gi i quy t bài toán. Ngoài raế ệ ứ ụ ể ả ế
các bài toán tính công c h c khi l c tác d ng bi n thiên theo th i gian, tínhơ ọ ự ụ ế ờ
nhi t l ng khi đi n tr thay đi….cũng c n đn ng d ng c a tích phân.ệ ượ ệ ở ổ ầ ế ứ ụ ủ
Trong đ tài này tôi đa ra m t s bài toán ề ư ộ ố “ ng d ng tích phân gi i m t sỨ ụ ả ộ ố
bài t p t tr ng”.ậ ừ ườ
2. Tên sáng ki n: “ếng d ng tích phân gi i m t s bài t p t tr ng”Ứ ụ ả ộ ố ậ ừ ườ
3. Tác gi sáng ki n:ả ế
- H và tên: Vũ Ng c Hoàngọ ọ
- Đa ch : Tr ng THPT Nguy n Th Giangị ỉ ườ ễ ị
- S đi n tho i: 0989.622.514 E_ mail: hoangvtvp@gmail.comố ệ ạ
4. Lĩnh v c áp d ng sáng ki n:ự ụ ế
Trong đ tài này tôi quan tâm đ c p đn các v n đ sau:ề ề ậ ế ấ ề
+ Các bài toán h t mang đi n chuy n đng trong t tr ng.ạ ệ ể ộ ừ ườ
+ Các bài toán thanh kim lo i trong t tr ng.ạ ừ ườ
+ Các bài toán khung dây r i trong t tr ng.ơ ừ ườ
1

+ H c sinh ph i đc trang b ki n th c v nguyên hàm và tích phânọ ả ượ ị ế ứ ề
tr c khi h c chuyên đ này.ướ ọ ề
N i dung c a đ tài n m trong ki n th c c a ch ng trình V t lí 11,ộ ủ ề ằ ế ứ ủ ươ ậ
V t lí 12 và m t s ki n th c toán h c l p 12. H c sinh l p 11 và 12 đu cóậ ộ ố ế ứ ọ ớ ọ ớ ề
th tham kh o.ể ả
5. Ngày sáng ki n đc áp d ng l n đuế ượ ụ ầ ầ : Ngày 12/12/2017
6. Mô t sáng ki nả ế
6.1. C s lí thuy tơ ở ế
1.1.1 Hi n t ng c m ng đi n tệ ượ ả ứ ệ ừ
a. Dòng đi n c m ngệ ả ứ : dòng đi n xu t hi n khi có s bi n đi t thôngệ ấ ệ ự ế ổ ừ
qua m ch đi n kín g i là dòng đi n c m ng.ạ ệ ọ ệ ả ứ
+ Đnh lu t Len-x v chi u c a dòng đi n c m ng:ị ậ ơ ề ề ủ ệ ả ứ
Dòng đi n c m ng có chi u sao cho t tr ng do nó sinh ra có tácệ ả ứ ề ừ ườ
d ng ch ng l i nguyên nhân đã sinh ra nó.ụ ố ạ
b. Su t đi n đng c m ngấ ệ ộ ả ứ : khi có s bi n đi t thông qua m t gi iự ế ổ ừ ặ ớ
h n b i m t m ch kín thì trong m ch xu t hi n su t đi n đng c m ng.ạ ở ộ ạ ạ ấ ệ ấ ệ ộ ả ứ
+ Đnh lu t Faraday v c m ng đi n t :ị ậ ề ả ứ ệ ừ
Đ l n c a su t đi n đng c m ng trong m ch kín t l v i t c độ ớ ủ ấ ệ ộ ả ứ ạ ỉ ệ ớ ố ộ
bi n thiên c a t thông qua m ch: ế ủ ừ ạ
c
t
ξ
∆Φ
= − ∆
.
1.1.2 Su t đi n đng c m ng trong m t đo n dây d n chuy nấ ệ ộ ả ứ ộ ạ ẫ ể
đng trong t tr ngộ ừ ườ
Khi m t đo n dây d n chuy n đng c t các đng s c t thì trongộ ạ ẫ ể ộ ắ ườ ứ ừ
đo n dây đó xu t hi n su t đi n đng c m ng.ạ ấ ệ ấ ệ ộ ả ứ
Bi u th c su t đi n đng c m ng trong đo n dây chuy n đng trongể ứ ấ ệ ộ ả ứ ạ ể ộ
t tr ng: ừ ườ
Bvl
c
.
1.1.3 M t s công th cộ ố ứ
2

+ Đnh lu t Jun – Lenx : Nhi t l ng Q t a ra trên m t đo n có đi n trị ậ ơ ệ ượ ỏ ộ ạ ệ ở
R khi có m t dòng đi n (bi n đi theo th i gian) ch y qua trong th i gian t:ộ ệ ế ổ ờ ạ ờ
2
0
t
Q Ri dt=
+ Công c a l c ủ ự
F
ur
th c hi n đc khi có m t d ch chuy n nh dx: ự ệ ượ ộ ị ể ỏ
0
.
x
x
A F dx=
+ Quãng đng v t đi đc trong chuy n đng m t chi u v i x = f(t):ườ ậ ượ ể ộ ộ ề ớ
0 0
.
x t
x t
S dx v dt= =
� �
+ Ph ng trình vi phân: dy = Adxươ (*)
Trong đó A là h ng s ; x,y là các đi l ng v t lí.ằ ố ạ ượ ậ
N u bài toán cho bi t đi u ki n ban đu (tr ng thái c a chuy n đngế ế ề ệ ầ ạ ủ ể ộ
t i th i đi m t = 0) thì l y nguyên hàm 2 v ph ng trình (*)ạ ờ ể ấ ế ươ
dy A dx=�� �
y = g(x) + C
Trong đó C là h ng s và đc xác đnh nh đi u ki n ban đu.ằ ố ượ ị ờ ề ệ ầ
N u bài toán cho bi t c đi u ki n ban đu và đi u ki n biên (Cho ế ế ả ề ệ ầ ề ệ
bi t giá tr c a y m t v trí nào đó c a x) thì ta s l y tích phân 2 v ph ngế ị ủ ở ộ ị ủ ẽ ấ ế ươ
trình (*):
0 0
yx
y x
dy A dx=
� �
(T đó tìm đc m i quan h gi a x và y).ừ ượ ố ệ ữ
6.2. Th c tr ng v n đự ạ ấ ề
Trong quá trình d y h c các chuyên đ nâng cao dành cho h c sinh gi i, tôiạ ọ ề ọ ỏ
nh n th y nhi u h c sinh còn lúng túng không bi t khi nào c n l y tích phânậ ấ ề ọ ế ầ ấ
hay nguyên hàm hai v c a 1 ph ng trình vi phân. Ngoài ra có m t s bàiế ủ ươ ộ ố
toán l y giá tr trung bình c a đi l ng c n tìm (xem ví d …) r t g ng épấ ị ủ ạ ượ ầ ụ ấ ượ
làm cho h c sinh ph i nh m t cách máy móc. Do đó v i nh ng bài t p nhọ ả ớ ộ ớ ữ ậ ư
v y tôi chuy n v vi c s d ng tích phân đ gi i quy t bài toán m t cách tậ ể ề ệ ử ụ ể ả ế ộ ự
nhiên và t o đc h ng thú h c t p cho h c sinh.ạ ượ ứ ọ ậ ọ
6.3. M t s bài toán đ xu tộ ố ề ấ
3

Đ th c hi n đc chuyên đ này tr c h t tôi dành 3 ti t d y nguyên ể ự ệ ượ ề ướ ế ế ạ
hàm, tích phân c b n cho h c sinh, 1 ti t d y ng d ng c a tích phân trong ơ ả ọ ế ạ ứ ụ ủ
v t lí và các công th c tích phân th ng g p trong v t lí ph thông (xem ph nậ ứ ườ ặ ậ ổ ầ
tóm t t lý thuy t). Sau đó tôi yêu c u h c sinh gi i các bài toán liên quan đn ắ ế ầ ọ ả ế
ng d ng c a nguyên hàm, tích phân (trong chuyên đ này tôi quan tâm gi i ứ ụ ủ ề ả
quy t các bài toán: chuy n đng c a h t mang đi n, c a thanh kim lo i trong ế ể ộ ủ ạ ệ ủ ạ
t tr ng).ừ ườ
6.3.1 Các bài t p s d ng nguyên hàmậ ử ụ
Bài 1. Trên m t bàn ph ng n m ngang đt m t khung dây d n hình chặ ẳ ằ ặ ộ ẫ ữ
nh t có các c nh a và b. Khung đc đt trong m t t tr ng có thành ph nậ ạ ượ ặ ộ ừ ườ ầ
c a vect c m ng t d c theo tr c z ch ph thu c vào to đô x theo quyủ ơ ả ứ ừ ọ ụ ỉ ụ ộ ạ
lu t: Bậz = B0(1 -
x
), trong đó B0 và
là các h ng s d ng (c nh b songằ ố ươ ạ
song v i tr c Ox còn Oz vuông góc v i m t ph ng khung). Truy n cho khungớ ụ ớ ặ ẳ ề
m t v n t c ộ ậ ố
0
v
d c theo tr c ox. B qua đ t c m c a khung dây. Hãy xácọ ụ ỏ ộ ự ả ủ
đnh kho ng cách mà khung dây đi đc cho đn khi d ng l i hoàn toàn. Bi tị ả ượ ế ừ ạ ế
đi n tr thu n c a khung là R.ệ ở ầ ủ
Bài gi iả
- Xét t i th i đi m t b t kì, c nh AB v trí có t a đ x, thành ph nạ ờ ể ấ ạ ở ị ọ ộ ầ
v n t c theo ph ng Ox là vậ ố ươ x.
- Áp d ng quy t c bàn tay ph i ta xác đnh đc chi u c a các su tụ ắ ả ị ượ ề ủ ấ
đi n đng c m ng trong m i c nh c a khung dây nh hình v .ệ ộ ả ứ ỗ ạ ủ ư ẽ
+ Xét chuy n đng c a khung dây theo tr c Oxể ộ ủ ụ
C nh BC và DA không t o ra su t đi n đng c m ng.ạ ạ ấ ệ ộ ả ứ
Su t đi n đng c m ng do c nh AB t o ra:ấ ệ ộ ả ứ ạ ạ
avxBavB xxABAB .)1(. 0
Su t đi n đng c m ng do c nh CD t o ra:ấ ệ ộ ả ứ ạ ạ
avbxBavB xxCDCD .)(1.. 0
4
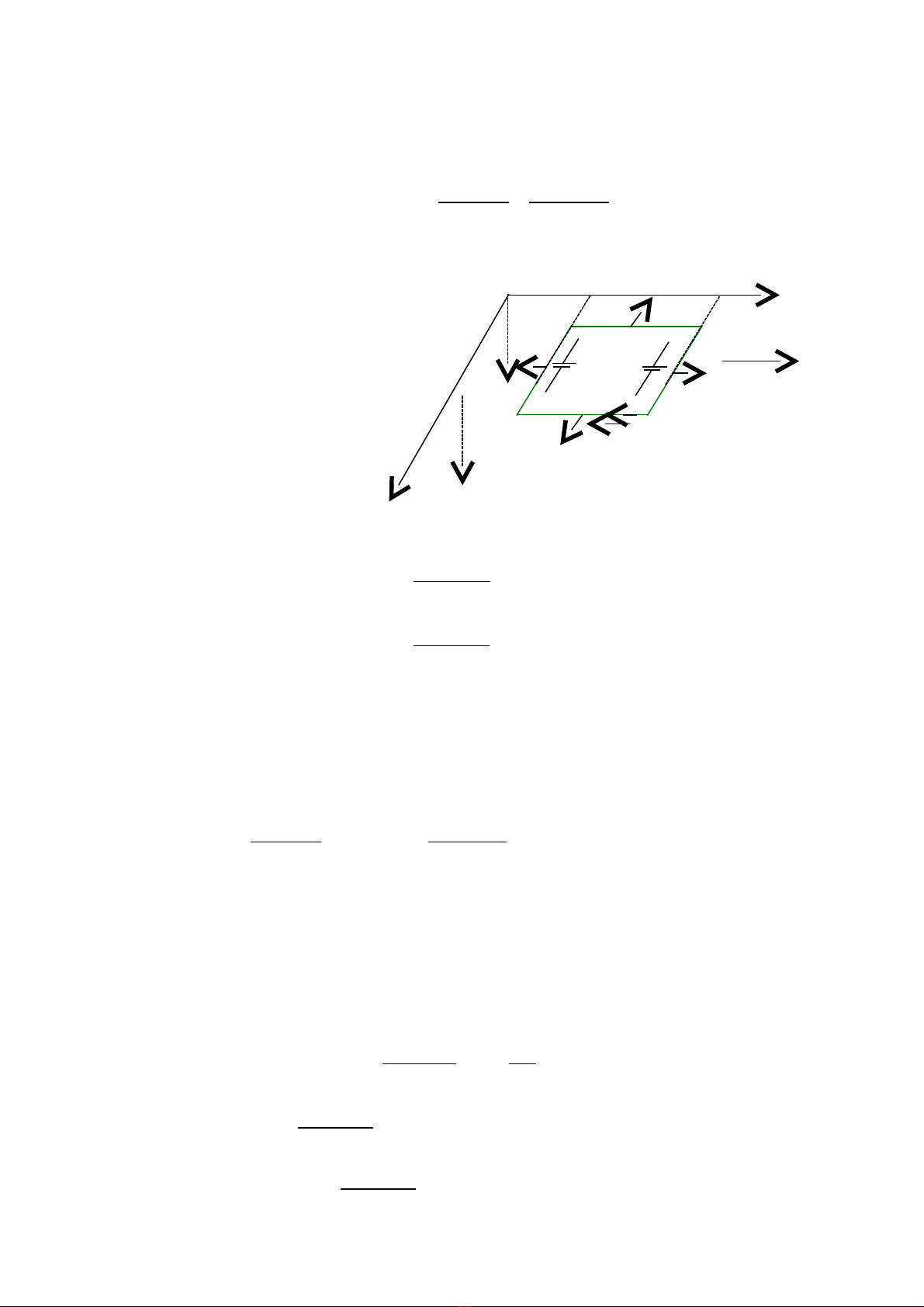
- G i c ng đ dòng đi n trong khung t i th i đi m xét là i. Ch nọ ườ ộ ệ ạ ờ ể ọ
chi u d ng trong m ch (trong khung dây) nh hình v . Áp d ng đnh lu tề ươ ạ ư ẽ ụ ị ậ
Ôm cho toàn m ch, ta đc:ạ ượ
R
bBav
R
ixCDAB .... 0
-Áp d ng quy t c bàn tay trái ta xác đnh đc l c t tác d ng lên c nh ụ ắ ị ượ ự ừ ụ ạ
AB, CD c a khung dây nh hình v .ủ ư ẽ
Ta có:
AB
x
ABAB B
R
vbaB
aiBF .
.
2
0
CD
x
CDCD B
R
vbaB
aiBF .
.
2
0
Xét khi c nh AB v trí x > 0 ạ ở ị
BAB > BCD
FAB > FCD
l c t t ng h p tác d ng lên khung dây có ph ng Ox ự ừ ổ ợ ụ ươ
Ft = FAB – FCD và
t
F
ng c h ng v i Oxượ ướ ớ
xCDAB
x
tv
R
abB
BB
R
vbaB
F
222
2
0
2
0
L c t tác d ng lên các c nh BC và DA có ph ng song song v i Oy,ự ừ ụ ạ ươ ớ
cùng đ l n nh ng ng c chi u nhau.ộ ớ ư ượ ề
Do đó, khung ch chuy n đng theo ph ng Oxỉ ể ộ ươ
Xét theo tr c Ox, áp d ng đnh lu t II Niut n cho khung, ta có:ụ ụ ị ậ ơ
- Ft = max
dt
dv
mv
R
abB x
x 2222
0
xx mdvdtv
R
abB 2222
0
(*)
xx dv
abB
Rm
dtv 2222
0
5
o
z
y
x
z
B
AD
CB
AD
F
CD
F
BC
F
AB
F
i
xx+b
AB
CD
0
v
















