
A. ĐT V N ĐẶ Ấ Ề
1. Lý do ch n đ tài.ọ ề
Trong c u trúc đ thi THPT Qu c gia hay các kì thi ch n h c sinh gi iấ ề ố ọ ọ ỏ
luôn có bài toán hình h c v ph ng pháp t a đ trong m t ph ng. Đó là ph nọ ề ươ ọ ộ ặ ẳ ầ
bài t p khó, có tính phân lo i, vì v y đa s h c sinh g p nhi u khó khăn trongậ ạ ậ ố ọ ặ ề
vi c gi i quy t các bài toán này.ệ ả ế
Ph ng pháp t a đ trong m t ph ng là ch ng trình hình h c 10, làươ ọ ộ ặ ẳ ươ ọ
ph n ti p n i v i hình h c ph ng THCS nh ng nhìn d i quan đi m đi sầ ế ố ớ ọ ẳ ở ư ướ ể ạ ố
và gi i tích. Nh v y m i bài toán hình h c t a đ ph ng đu mang b n ch tả ư ậ ỗ ọ ọ ộ ẳ ề ả ấ
c a m t bài toán hình h c ph ng nào đó. Tuy nhiên khi gi i các bài toán hìnhủ ộ ọ ẳ ả
h c t a đ trong m t ph ng, h c sinh th ng khó v n d ng đc các tínhọ ọ ộ ặ ẳ ọ ườ ậ ụ ượ
ch t c a hình h c ph ng vì hình h c ph ng th ng khó và các tính ch t đóấ ủ ọ ẳ ọ ẳ ườ ấ
th ng khó phát hi n trong các bài toán v ph ng pháp t a đ. Bên c nh đóườ ệ ề ươ ọ ộ ạ
phép bi n hình là m ng ki n th c khó, h c sinh ng i h c. Vì v y, th c t yêuế ả ế ứ ọ ạ ọ ậ ự ế
c u ph i trang b cho h c sinh m t h th ng các ph ng pháp suy lu n đ gi iầ ả ị ọ ộ ệ ố ươ ậ ể ả
các bài toán hình h c ph ng hi u qu h n. ọ ẳ ệ ả ơ
V i nh ng lý do đó, tôi đa ra sáng ki n kinh nghi m “ớ ữ ư ế ệ Phép đi x ngố ứ
tr c trong m t s bài toán v ph ng pháp t a đ trong m t ph ngụ ộ ố ề ươ ọ ộ ặ ẳ ” nh mằ
giúp h c sinh có đnh h ng t t h n đ gi i các bài toán v t a đ trong m tọ ị ướ ố ơ ể ả ề ọ ộ ặ
ph ng và nh m nâng cao ch t l ng gi ng d y, giúp h c sinh đt k t qu caoẳ ằ ấ ượ ả ạ ọ ạ ế ả
h n trong các kì thi.ơ
2. M c đích nghiên c u.ụ ứ
Tìm ra ph ng pháp d y h c phù h p v i h c sinh tr ng THPT. Làmươ ạ ọ ợ ớ ọ ườ
cho h c sinh hi u, d nh và v n d ng đc các tính ch t c a hình h c ph ngọ ể ễ ớ ậ ụ ượ ấ ủ ọ ẳ
vào gi i quy t các bài toán v t a đ trong m t ph ng. H c sinh tìm đc m iả ế ề ọ ộ ặ ẳ ọ ượ ố
liên h gi a các tính ch t c a phép đi x ng tr c v i các tính ch t hình h cệ ữ ấ ủ ố ứ ụ ớ ấ ọ
ph ng, v i b n ch t hình h c c a bài toán t a đ trong m t ph ng.ẳ ớ ả ấ ọ ủ ọ ộ ặ ẳ
3. Ph m vi nghiên c u.ạ ứ
Nghiên c u và v n d ng m t s tính ch t c a phép đi x ng tr c vàoứ ậ ụ ộ ố ấ ủ ố ứ ụ
gi i các bài toán v ph ng pháp t a đ trong m t ph ng cho h c sinh kh iả ề ươ ọ ộ ặ ẳ ọ ố
10, kh i 11 và h c sinh ôn thi đi h c. ố ọ ạ ọ
1

B. N I DUNGỘ
1. C s lý lu nơ ở ậ
1.1. M t s tính ch t c a m t s phép đi x ng tr c.ộ ố ấ ủ ộ ố ố ứ ụ
- Phép đi x ng tr c: Đi m M và M’ (M ố ứ ụ ể M’) đc g i là đi x ng v iượ ọ ố ứ ớ
nhau qua đng th ng d n u d là đng trung tr c c a đo n MM’.ườ ẳ ế ườ ự ủ ạ
- Phép đi x ng tr c là phép d i hình, t c là nó b o toàn kho ng cách gi aố ứ ụ ờ ứ ả ả ữ
hai đi m b t kì.ể ấ
- H qu : Phép bi n hình bi n 3 đi m th ng hàng thành ba đi m th ng hàngệ ả ế ế ể ẳ ể ẳ
và không làm thay đi th t c a chúng; bi n m t đo n th ng thành m t đo nổ ứ ự ủ ế ộ ạ ẳ ộ ạ
th ng b ng nó; bi n m t đng th ng thành m t đng th ng; bi n m t tiaẳ ằ ế ộ ườ ẳ ộ ườ ẳ ế ộ
thành m t tia; bi n m t góc thành m t góc b ng nó; bi n m t tam giác b ngộ ế ộ ộ ằ ế ộ ằ
m t tam giác b ng nó; bi n m t đng tròn b ng m t đng tròn b ng nó.ộ ằ ế ộ ườ ằ ộ ườ ằ
1.2. M t s v n đ v ph ng pháp t a đ trong m t ph ng.ộ ố ấ ề ề ươ ọ ộ ặ ẳ
- Cho A(xA; yA), B(xB; yB).
Khi đó:
( ; )
B A B A
AB x x y y= − −
uuur
Trung đi m M c a đo n AB có t a đ đc xác đnh Mể ủ ạ ọ ộ ượ ị
;
2 2
A B A B
x x y y+ +
� �
� �
� �
- Cho đng th ng Δ có véct pháp tuy n ườ ẳ ơ ế
(A;B)n=
ur
, đi qua M(xo;yo) có
ph ng trình A(x – xươ o) + B(y – yo) = 0 hay Ax + By + C = 0 (A2 + B2 0)
- Đng th ng Δ có vect ch ph ng ườ ẳ ơ ỉ ươ
( ; )u a b
=
ur
thì có vect pháp tuy nơ ế
( ; )n b a
= −
ur
.
- Cho đng th ng Δ: ườ ẳ ax+ by + c = 0 và đi m M(xể0; y0). Kho ng cách t Mả ừ
đn Δ đc xác đnh b i: ế ượ ị ở
0 0
2 2
( ; ) ax by c
d M
a b
+ +
∆ = +
- Đng tròn tâm I(a; b) có bán kính R có ph ng trình: (x – a)ườ ươ 2 + (y – b)2 = R2.
2. Th c tr ng c a v n đ nghiên c u.ự ạ ủ ấ ề ứ
2

M i chúng ta đu nh n th y Toán h c là môn h c khó, không ph i h cỗ ề ậ ấ ọ ọ ả ọ
sinh nào cũng ti p thu t t ki n th c toán h c. Các bài toán v t a đ trong m tế ố ế ứ ọ ề ọ ộ ặ
ph ng trong các đ thi đi h c, cao đng l i càng làm cho h c sinh lúng túng vìẳ ề ạ ọ ẳ ạ ọ
không bi t đnh h ng t đâu. Nhi u h c sinh th ng có thói quen không t t làế ị ướ ừ ề ọ ườ ố
đc đ ch a kĩ đã làm ngay, có khi s th nghi m đó cũng đa đn k t quọ ề ư ự ử ệ ư ế ế ả
nh ng hi u su t không cao. V i tình hình y đ giúp h c sinh đnh h ng t tư ệ ấ ớ ấ ể ọ ị ướ ố
h n trong quá trình gi i toán hình h c to đ trong m t ph ng, ng i giáo viênơ ả ọ ạ ộ ặ ẳ ườ
c n t o cho h c sinh thói quen xem xét bài toán d i nhi u góc đ, khai thácầ ạ ọ ướ ề ộ
các y u t đc tr ng hình h c c a bài toán đ tìm l i gi i. Trong đó vi c hìnhế ố ặ ư ọ ủ ể ờ ả ệ
thành cho h c sinh kh năng t duy theo các ph ng pháp gi i là m t đi u c nọ ả ư ươ ả ộ ề ầ
thi t. Vi c tr i nghi m qua quá trình gi i toán s giúp h c sinh hoàn thi n kế ệ ả ệ ả ẽ ọ ệ ỹ
năng đnh h ng và gi i toán.ị ướ ả
C n nh n m nh m t đi u r ng, đa s các h c sinh sau khi tìm đc m tầ ấ ạ ộ ề ằ ố ọ ượ ộ
l i gi i cho bài toán hình h c to đ trong m t ph ng th ng không suy nghĩ,ờ ả ọ ạ ộ ặ ẳ ườ
đào sâu thêm. H c sinh th ng không chú ý đn b n ch t hình h c ph ng c aọ ườ ế ả ấ ọ ẳ ủ
bài toán nên m c dù làm r t nhi u bài toán hình h c to đ nh ng v n khôngặ ấ ề ọ ạ ộ ư ẫ
phân lo i đc d ng toán c b n cũng nh b n ch t c a bài toán. Th m chíạ ượ ạ ơ ả ư ả ấ ủ ậ
m t bài toán t ng t nhau xu t hi n trong nhi u đ thi mà h c sinh v n làmộ ươ ự ấ ệ ề ề ọ ẫ
mi t mài nh l n đu tiên gi i nó, b i không nh n bi t đc d ng toán này đóệ ư ầ ầ ả ở ậ ế ượ ạ
t ng làm.ừ
V i th c tr ng đã ch ra, thông th ng h c sinh s d dàng cho l i gi iớ ự ạ ỉ ườ ọ ẽ ễ ờ ả
đi v i các bài toán có c u trúc đn gi n. Còn khi đa ra bài toán khác m tố ớ ấ ơ ả ư ộ
chút c u trúc c b n h c sinh th ng t ra r t lúng túng và không bi t đnhấ ơ ả ọ ườ ỏ ấ ế ị
h ng tìm l i gi i bài toán. T đó, hi u qu gi i toán c a h c sinh b h n chướ ờ ả ừ ệ ả ả ủ ọ ị ạ ế
r t nhi u. Tr c th c tr ng đó c a h c sinh, tôi th y c n thi t ph i hình thànhấ ề ướ ự ạ ủ ọ ấ ầ ế ả
cho h c sinh thói quen xem xét bài toán hình h c to đ trong m t ph ng theoọ ọ ạ ộ ặ ẳ
b n ch t hình h c ph ng. Và vì v y song song v i các l i gi i cho bài toánả ấ ọ ẳ ậ ớ ờ ả
hình h c to đ trong m t ph ng, tôi luôn yêu c u h c sinh ch ra b n ch t vàọ ạ ộ ặ ẳ ầ ọ ỉ ả ấ
bài toán hình ph ng t ng ng, t đó phân tích ng c l i cho bài toán v aẳ ươ ứ ừ ượ ạ ừ
gi i.ả
Trong sáng ki n kinh nghi m này, tôi đa ra m t s n i dung v n d ngế ệ ư ộ ố ộ ậ ụ
phép đi x ng tr c đ tìm ra b n ch t, tính ch t hình h c c a bài toán t a đố ứ ụ ể ả ấ ấ ọ ủ ọ ộ
ph ng, đ đnh h ng, tìm l i gi i cho các bài toán đó. Qua đó giúp h c sinhẳ ể ị ướ ờ ả ọ
3

nh n th c đc r ng: “M i bài toán hình h c to đ trong m t ph ng luônậ ứ ượ ằ ỗ ọ ạ ộ ặ ẳ
ch a đng m t bài toán hình ph ng t ng ng”. Vì v y phân tích b n ch tứ ự ộ ẳ ươ ứ ậ ả ấ
c a bài toán hình h c ph ng đ b tr cho vi c gi i bài toán hình h c to đủ ọ ẳ ể ổ ợ ệ ả ọ ạ ộ
trong m t ph ng là m t suy nghĩ có ch đích, giúp h c sinh ch đng h nặ ẳ ộ ủ ọ ủ ộ ơ
trong vi c tìm ki m l i gi i cũng nh phân lo i m t cách t ng đi các bàiệ ế ờ ả ư ạ ộ ươ ố
toán hình h c to đ trong m t ph ng.ọ ạ ộ ặ ẳ
Trên th c t , tôi đã kh o sát ch t l ng h c t p c a h c sinh (v v nự ế ả ấ ượ ọ ậ ủ ọ ề ấ
đ gi i các bài toán ph ng pháp t a đ trong m t ph ng) và đã thu đc k tề ả ươ ọ ộ ặ ẳ ượ ế
qua nh sau:ư
L pớSĩ sốGi iỏKháTrung bình Y uếKém
SL % SL % SL % SL % SL %
10A1 43 7 16.3 18 41.9 13 30.2 511.6 00
11B2 40 6 15 17 42,5 10 25 717,5 00
Nh v y rõ ràng s l ng h c sinh n m b t d ng toán này không nhi uư ậ ố ượ ọ ắ ắ ạ ề
v i lý do không nh n d ng, không đnh h ng đc cách gi i rõ ràng.ớ ậ ạ ị ướ ượ ả
3. Các bi n pháp th c hi n ệ ự ệ
3.1. Các yêu c u chungầ
- Đi u tra h c l c c a h c sinh qua các bài ki m tra.ề ọ ự ủ ọ ể
- T ch c ôn t p vào các bu i ngo i khoá nh m tăng th i l ng luy n t pổ ứ ậ ổ ạ ằ ờ ượ ệ ậ
gi i toán.ả
- Khi ra bài t p cho h c sinh, giáo viên yêu c u h c sinh th c hi n đy đ m tậ ọ ầ ọ ự ệ ầ ủ ộ
s n i dung sau:ố ộ
+) Đc k n i dung bài toán.ọ ỹ ộ
+) Nh n d ng bài toán thu c d ng toán nào, th c hi n phép "quy l vậ ạ ộ ạ ự ệ ạ ề
quen".
+) Xác đnh rõ yêu c u bài toán.ị ầ
+) Xác đnh đúng gi thi t, k t lu n (có th vi t gi thi t d i d ngị ả ế ế ậ ể ế ả ế ướ ạ
khác đc không?)ượ
+) T mình ti n hành gi i bài toán.ự ế ả
+) Ki m tra xem đã v n d ng h t gi thi t ch a, trong bài s d ngể ậ ụ ế ả ế ư ử ụ
nh ng ki n th c nào?ữ ế ứ
+) Đi chi u v i cách gi i c a b n, c a th y.ố ế ớ ả ủ ạ ủ ầ
4
+) Tìm thêm các l i gi i khác cho bài toán (n u có).ờ ả ế
+) Rút ra kinh nghi m cho b n thân.ệ ả
3.2. Th c ựhành qua các d ng toánạ
Trong ph n này, tôi đa ra m t s d ng toán v v n d ng phép điầ ư ộ ố ạ ề ậ ụ ố
x ng tr c vào gi i các bài toán t a đ trong m t ph ng.ứ ụ ả ọ ộ ặ ẳ
Các bài toán mang d u hi u c a phép đi x ng tr c.ấ ệ ủ ố ứ ụ
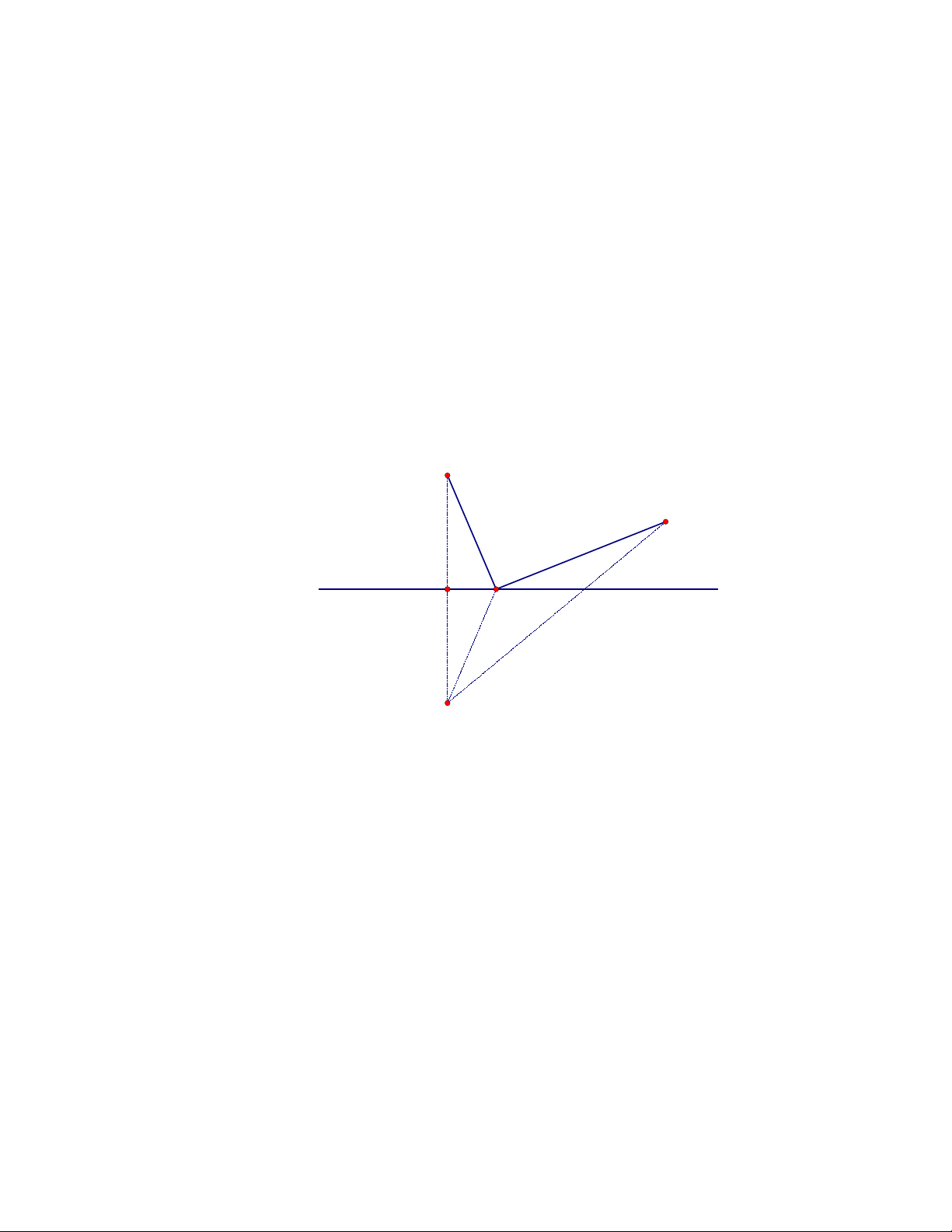
Bài toán g c:ố Cho hai đi m A, B n m v cùng phía c a đng th ng d. Tìmể ằ ề ủ ườ ẳ
M trên d sao cho AM + BM ng n nh t.ắ ấ
Cách gi i: ả
G i A’ là đi m đi x ng v i A qua d. Khi đó v i m i M ọ ể ố ứ ớ ớ ọ d, ta có: MA =
MA’
d
A
A'
B
M
MA + MB = MA’ + MB ≥ A’B. V y MA + MB đt giá tr nh nh t khi A’,ậ ạ ị ỏ ấ
M, B th ng hàng hay M là giao đi m c a đng th ng A’B v i d.ẳ ể ủ ườ ẳ ớ
T đó, ta có th áp d ng cách gi i trên vào các bài toán t a đ trong m t ph ngừ ể ụ ả ọ ộ ặ ẳ
nh sau:ư
Bài 1.
Trong m t ph ng v i h t a đ Oxy, cho đng th ng d có ph ngặ ẳ ớ ệ ọ ộ ườ ẳ ươ
trình: 2x – y + 5 = 0 và hai đi m A(2; - 1), B(1; 2).ể
Tìm t a đ đi m M thu c d sao cho chu vi ΔMAB đt giá tr nh nh t.ọ ộ ể ộ ạ ị ỏ ấ
Giáo viên h ng d n:ướ ẫ
- Yêu c u h c sinh xác đnh d ng toán, phân tích gi thi t c a bài toán.ầ ọ ị ạ ả ế ủ
- Ki m tra xem A và B có cùng phía v i d hay không?ể ớ
- T đó có th v n d ng bài toán t ng h p trên.ừ ể ậ ụ ổ ợ ở
5


























