
http://ebook.here.vn - Thư viện sách trực tuyến
SỞ GD – ðT BÌNH ðỊNH KỲ THI THỬ ðẠI HỌC NĂM HỌC 2009-2010 (lần 2)
TRƯỜNG THPT CHUYÊN LÊ QUÝ ðÔN Môn: Toán – Khối A, B, V
Thời gian làm bài: 180 phút
Ngày thi: 03/04/2010
I. PHẦN CHUNG CHO TẤT CẢ THÍ SINH: ( 7 ñiểm)
Câu I: (2 ñiểm) Cho hàm số
2 1
1
x
y
x
−
=
+
1. Khảo sát sự biến thiên và vẽ ñồ thị (C) của hàm số.
2. Chứng minh rằng ñường thẳng d: y = - x + 1 là truc ñối xứng của (C).
Câu II
: (2 ñiểm)
1 Giải phương trình:
4cos3xcosx - 2cos4x - 4cosx + tan t anx + 2
2
0
2sinx - 3
x
=
2. Giải bất phương trình:
2 2 2
2
3 2.log 3 2.(5 log 2)
x
x x x x x− + ≤ − + −
Câu III
: ( 1 ñiểm).
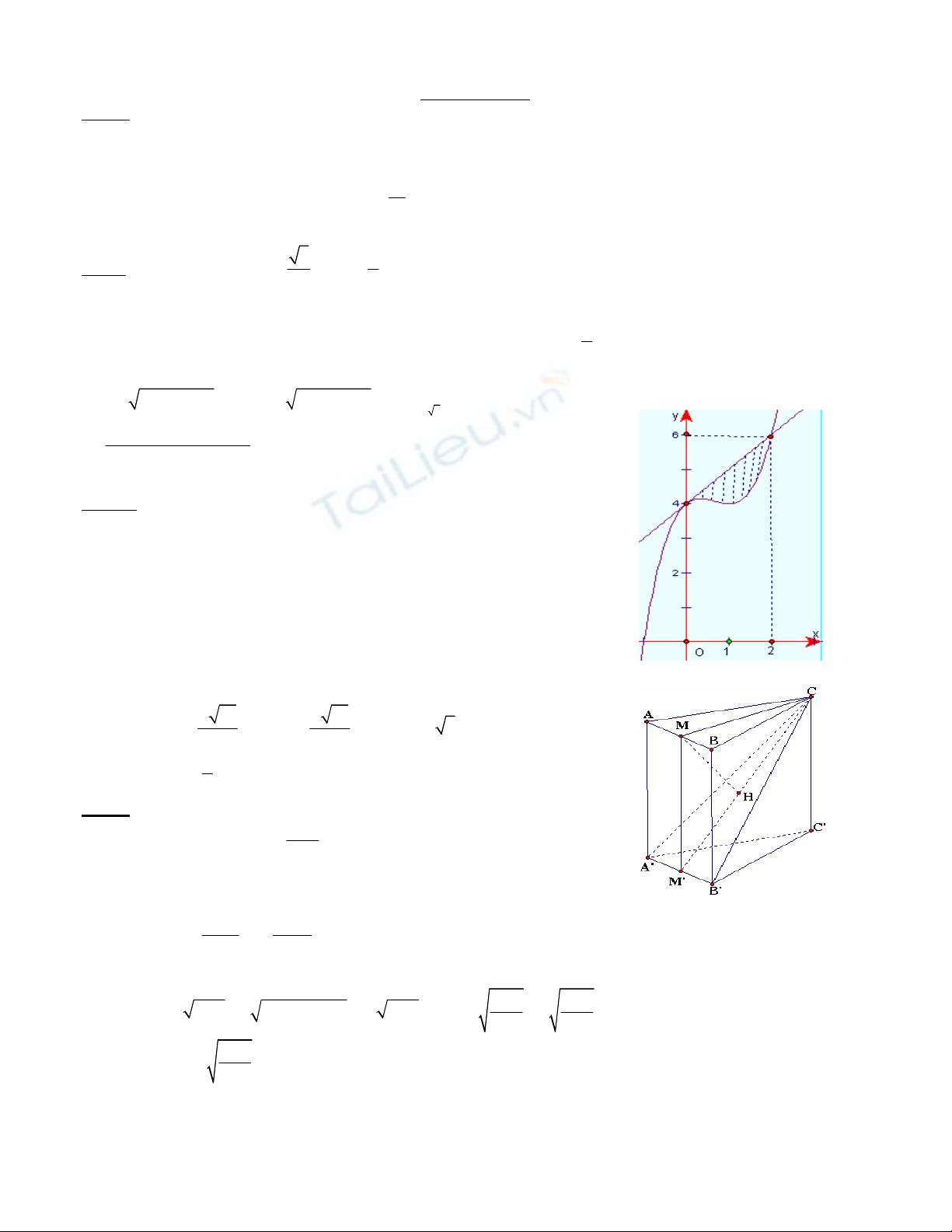
Gọi (H) là hình phẳng giới hạn ñồ thi (C) của hàm sô y = x
3
– 2x
2
+ x + 4 và tiếp tuyến của (C) tại ñiểm
có hoành ñộ
x
0
= 0. Tính thể tích của vật thể tròn xoay ñược tạo thành khi quay hình phẳng (H) quanh
trục Ox.
Câu IV
: (1ñiểm) Cho hình lặng trụ tam giác ñều ABC.A’B’C’ có cạnh ñáy bằng
a
. Biết khoảng cách giữa hai
ñường thẳng AB và A’C bằng
15
5
a. Tính thể tích của khối lăng trụ
Câu V:(1ñiểm) Tìm m ñể hệ phương trình sau có nghiệm:
4
(2 1)[ln(x + 1) - lnx] = (2y + 1)[ln(y +
1) - lny] (1)
y-1 2 ( 1)( 1) 1 0 (2)
x
y x m x
+
− + − + + =
II. PHẦN RIÊNG
(3 ñiểm): Thí sinh chỉ làm một trong hai phần (Phần 1 hoặc phần 2
Phần 1: Theo chương trình chuẩn
Câu VI.a:
( 2 ñiểm).
1. Trong mặt phẳng Oxy cho ñường tròn (C): x
2
+ y
2
= 1; và phương trình: x
2
+ y
2
– 2(m + 1)x + 4my –
5 = 0 (1) Chứng minh rằng phương trình (1) là phương trình của ñường tròn với mọi m.Gọi các ñường
tròn tương ứng là (C
m
). Tìm m ñể (C
m
) tiếp xúc với (C).
2. Trong không gian Oxyz cho ñường thẳng d: 1 2
1 1 1
x y z
− +
= =
và mặt phẳng (P): 2x + y – 2z + 2 = 0.
Lập phương trình mặt cầu (S) có tâm nằm trên d, tiếp xúc với mặt phẳng (P) và ñi qua ñiểm A(2; - 1;0)
Câu VII.b: ( 1 ñiểm).
Cho x; y là các số thực thoả mãn x
2
+ y
2
+ xy = 1. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
P = 5xy – 3y
2
Phần 2: Theo chương trình nâng cao:
Câu VI.b:
( 2 ñiểm).
1.Trong không gian Oxyz cho ñiểm A(3;2;3) và hai ñường thẳng 1
2 3 3
:
1 1 2
x y z
d
− − −
= =
−
và
2
1 4 3
:
1 2 1
x y z
d
− − −
= =
−
. Chứng minh ñường thẳng d
1
; d
2
và ñiểm A cùng nằm trong một mặt phẳng.
Xác ñịnh toạ ñộ các ñỉnh B và C của tam giác ABC biết d
1
chứa ñường cao BH và d
2
chứa ñường trung
tuyến CM của tam giác ABC.
2.Trong mặt phẳng Oxy cho elip (E) có hai tiêu ñiểm
1 2
( 3;0); ( 3;0)
F F−
và ñi qua ñiểm
1
3;
2
A
.
Lập phương trình chính tắc của (E) và với mọi ñiểm M trên elip, hãy tính biểu thức:
P = F
1
M
2
+ F
2
M
2
– 3OM
2
– F
1
M.F
2
M
Câu VII.b:
( 1 ñiểm). Tính giá trị biểu thức:
0 2 2 4 2 1004 2008 1005 2010
2010 2010 2010 2010 2010 2010
3 3 ... ( 1) ... 3 3
k k
S C C C C C C= − + + + − + + −
------------------------------------Hết --------------------------------------
http://ebook.here.vn - Thư viện sách trực tuyến
Hướng dẫn giải
Câu I:
2. Giao ñiểm hai tiệm cận I(- 1;2) . Chuyển hệ trục toạ ñộ Oxy --> IXY:
1
2
x X
y Y
= −
= +
Hàm số ñã cho trở thành : Y =
3
X
−
hàm số ñồng biến nê (C) ñối xứng qua ñường thẳng Y = - X
Hay y – 2 = - x – 1
⇔
y = - x + 1
Câu II: 1. ðiều kiện:
3
sinx
2
≠
và
os 0
2
x
c
≠
và cosx ≠ 0
Biến ñổi pt về: 4cos
3
x - 4 cos
2
x – cosx + 1 = 0
osx = 1
1
cosx =
2
c
⇔
±
2. ðiều kiện 0 < x < 1 hoặc x ≥ 2.
2 2 2
2
3 2.log 3 2.(5 log 2)
x
x x x x x− + ≤ − + −
2
2 2
2
2log 5log 2
0
log
x x
x
− +
⇒ ≤
Nghiệm: 0 < x < 1 hoặc 2 ≤ x ≤ 4
Câu III: Phương trình tiếp tuyến : y = x + 4
Phương trình hoành ñộ giao ñiểm: x
3
– 2x
2
= 0
0
2
x
x
=
⇔
=
V =
2 2
2 3 2 2
0 0
( 4) ( 2 4)
x dx x x x dx
π π
+ − − + +
∫ ∫
Câu IV:
Gọi M; M’ lần lượt là trung ñiểm của AB và A’B’. Hạ MH ⊥ M’C
AB // (A’B’C) ==> d(AB,A’C) = MH
HC =
15
10
a; M’C =
15
2
a ; MM’ =
3
a
Vậy V =
3
3
4
a
Câu V
: ðặt f(x) = (2x + 1)[ln(x + 1) – lnx] TXð: D = [0;+∞)
=
1
(2 1)ln
x
x
x
+
+
Gọi x
1
; x
2
∈ [0;+∞) với x
1
> x
2
Ta có :
1 2
1 2
1 2
1 2
2 1 2 1 0
( ) ( )
1 1
ln ln 0
x x
f x f x
x x
x x
+ > + >
⇒ >
+ +
> >
: f(x) là hàm số tăng
Từ phương trình (1) ⇒ x = y
(2)
4
1 2 ( 1)( 1) 1 0
x x x m x
⇒ − − − + + + =
4
1 1
2 0
1 1
x x m
x x
− −
⇔ − + =
+ +
ðặt X =
4
1
1
x
x
−
+
==> 0 ≤ X < 1
Vậy hệ có nghiêm khi phương trình: X
2
– 2X + m = 0 có nghiệm 0 ≤ X < 1
ðặt f(X) = X
2
– 2X == > f’(X) = 2X – 2
==> hệ có nghiêm ⇔ -1 < m ≤ 0

http://ebook.here.vn - Thư viện sách trực tuyến
Câu VI.a
1. (C) có tâm O(0;0) bán kính R = 1, (C
m
) có tâm I(m +1; -2m) bán kính
2 2
' ( 1) 4 5
R m m
= + + +
OI
2 2
( 1) 4
m m
= + + , ta có OI < R’
Vậy (C) và (C
m
) chỉ tiếp xuc trong.==> R’ – R = OI ( vì R’ > R)
Giải ra m = - 1; m = 3/5
2. Gọi I là tâm của (S) ==> I(1+t;t – 2;t)
Ta có d(I,(P)) = AI == > t = 1; t = 7/13
(S
1
): (x – 2)
2
+ (y + 1)
2
+ (z – 1)
2
= 1; (S
2
): (x – 20/13)
2
+ (y + 19/13)
2
+ (z – 7/13)
2
= 121/139
Câu VII.a
2
2 2
5 3
xy y
P
x xy y
−
=
+ +
Với y = 0 ==> P = 0
Với y ≠ 0 ñặt x = ty; ta có:
2
2
5 3
( 5) 3 0
1
t
P Pt P t P
t t
−
= ⇔ + − + + =
+ +
(1)
+ P = 0
thì phương trình ( 1) có nghiệm t = 3/5
+ P ≠ 0 thì phương trình ( 1) có nghiệm khi và chỉ khi
∆’ = - P
2
– 22P + 25
≥
0 ⇔ - 25/3 ≤ P ≤ 1
Từ ñó suy maxP , minP
Câu VI.b:
1. d
1
qua M
0
(2;3;3) có vectơ chỉ phương
(1;1; 2)
a
= −
r
d
2
qua M
1
(1;4;3) có vectơ chỉ phương
(1; 2;1)
b= −
r
Ta có
0 1
, 0 , 0
a b va a b M M
≠ =
urr r r r uuuuuur
(d
1
,d
2
) : x + y + z – 8 = 0 ==> A ∈ (d
1
,d
2
)
B(2 + t;3 + t;3 - 2t); 5 5
; ;3
2 2
t t
M t
+ +
−
∈ d
2
==> t = - 1 ==> M(2;2;4)
C( 1+t;4-2t;;3+t) :
AC a
⊥
uuur r
==> t = 0 ==> C(1;4;2)
2. (E):
2 2
2 2 2 2
3 1
1 1
4
x y
a b a b
+ = ⇒ + =
, a
2
= b
2
+ 3 ==>
2 2
1
4 1
x y
+ =
P = (a + ex
M
)
2
+ (a – ex
M
)
2
– 2(
2 2
M M
x y
+
) – (a
2
– e
2
2
M
x
) = 1
Câu VII.b:
Ta có:
(
)
(
)
( )
2010 2010
0 2 2 4 2 1004 2008 1005 2010
2010 2010 2010 2010 2010 2010
1 3 1 3 2 3 3 ... ( 1) 3 ... 3 3
k k k
i i C C C C C C+ + − = − + + + − + + −
Mà
( ) ( )
2010 2010 2010 2010
2010 2010 -2010 -2010
1 3 1 3 2 ( os in ) 2 os in
3 3 3 3
i i c s c s
π π π π
+ + − = + + +
=
(
)
2010 2010
2.2 os670 2.2
c
π
=
Vậy S = 2
2010
-----------------------------------------------------










![Chuyển đổi số trong giáo dục đại học: Tiền đề và thách thức [Phân tích]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251215/longtimenosee01/135x160/70371765794622.jpg)





















![Đề thi tiếng Anh tốt nghiệp THPT 2025 (Chính thức) kèm đáp án [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250627/laphong0906/135x160/9121751018473.jpg)



