Tìm đ ng đi ng n nh t v i đ nh tuy n Dijkstraườ ắ ấ ớ ị ế
Bài viết này xin giới thiệu với các bạn mới làm quen với tin học và thuật giải một thuật toán đơn giản nhưng lại
có hiệu quả rất lớn trong việc tìm đường đi ngắn nhất trong đồ thị. Đó là thuật toán Dijkstra. Đây là thuật toán
đã đăng tải trên tạp chí tin học & nhà trường từ những số đầu tiên nhưng bài viết này sẽ đăng tải đầy đủ về bài
toán, phương thức đưa ra thuật giải cũng như đoạn chương trình đầy đủ. Rất thích hợp với những bạn mới làm
quen với những thuật toán kinh điển.
Dijkstra là thu t toán đ nh tuy n đ n gi n đ tìm đ ng đi ng n nh t gi a 2 đi m b t kỳ. Không m tậ ị ế ơ ả ể ườ ắ ấ ữ ể ấ ấ
tính t ng quát, ta coi m i đi m (nút m ng) là m t đ nh c a m t đ th , ta s dùng thu t toán Dijkstra đổ ỗ ể ạ ộ ỉ ủ ộ ồ ị ẽ ậ ể
gi i quy t bài toán tìm đ ng đi ng n nh t gi a 2 đi m nh sau:ả ế ườ ắ ấ ữ ể ư
Bài toán: Cho đ th G v i t p đ nh V và t p các c nh E (đ th có h ng ho c vô h ng). M i c nhồ ị ớ ậ ỉ ậ ạ ồ ị ướ ặ ướ ỗ ạ
c a đ th đ c gán m t nhãn (giá tr không âm), nhãn này còn đ c g i là giá tr c a c nh. Cho tr củ ồ ị ượ ộ ị ượ ọ ị ủ ạ ướ
m t đ nh xác đ nh v, g i là đ nh ngu n. Tìm đ ng đi ng n nh t t đ nh v đ n các đ nh còn l i c a G.ộ ỉ ị ọ ỉ ồ ườ ắ ấ ừ ỉ ế ỉ ạ ủ
(T c là tìm đ ng đi t v đ n các đ nh còn l i v i t ng các giá c a các c nh trên đ ng đi là nh nh t).ứ ườ ừ ế ỉ ạ ớ ổ ủ ạ ườ ỏ ấ
N u nh đ th có h ng thì đ ng đi này là đ ng đi có h ng. ế ư ồ ị ướ ườ ườ ướ
Thu t toán Dijkstraậ: Ta có th gi i bài toán b ng cách xác đ nh m t t p h p S ch a các đ nh màể ả ằ ị ộ ậ ợ ứ ỉ
kho ng cách ng n nh t t nó đ n đ nh ngu n v đã bi t. Kh i đ u S = { V }. Sau đó t i m i b c ta sả ắ ấ ừ ế ỉ ồ ế ở ầ ạ ỗ ướ ẽ
thêm vào S các đ nh mà kho ng cách t nó đ n v là ng n nh t. V i gi thi t r ng m i cung có m t giáỉ ả ừ ế ắ ấ ớ ả ế ằ ỗ ộ
tr không âm thì ta luôn luôn tìm đ c m t đ ng đi ng n nh t nh v y mà ch đi qua các đ nh đã t n t iị ượ ộ ườ ắ ấ ư ậ ỉ ỉ ồ ạ
trong S. Ð d dàng chi ti t hóa gi i thu t, gi s G có n đ nh và nhãn trên m i cung đ c l u trongể ễ ế ả ậ ả ử ỉ ỗ ượ ư
m ng C, t c là C[i, j] b ng giá tr (có th xem là đ dài) c a cung (i, j). N u i và j không có cung n i thì taả ứ ằ ị ể ộ ủ ế ố
cho C[i, j] =Ġ. Ta s dùng m t m ng D có n ph n t đ l u đ dài c a đ ng đi ng n nh t t v đ nẽ ộ ả ầ ử ể ư ộ ủ ườ ắ ấ ừ ế
m i đ nh c a đ th . Kh i đ u thì giá tr này chính là đ dài c nh (v, i), t c D[i] = C[v, i]. T i m i b cỗ ỉ ủ ồ ị ở ầ ị ộ ạ ứ ạ ỗ ướ
c a gi i thu t thì D[i] s l u đ dài đ ng đi ng n nh t t đ nh v đ n đ nh i, đ ng đi này ch đi qua cácủ ả ậ ẽ ư ộ ườ ắ ấ ừ ỉ ế ỉ ườ ỉ
đ nh đã có trong S. ỉ
Ð cài đ t gi i thu t d dàng, ta gi s các đ nh c a đ th đ c đánh s t 1 đ n n và đ nh ngu n làể ặ ả ậ ễ ả ử ỉ ủ ồ ị ượ ố ừ ế ỉ ồ
đ nh 1. D i đây là gi i thu t ỉ ướ ả ậ Dijkstra đ gi i bài toán trên : ể ả
<!--[if !supportLineBreakNewLine]-->
<!--[endif]-->
procedure Dijkstra;
begin
S := [1] ; { S ch ch a đ nh ngu n } ỉ ứ ỉ ồ
for i:=2 to n do
D[i] := C[1, i] ; { Kh i đ u các giá tr cho D } ở ầ ị
for i:=1 to n - 1 do
begin
L y đ nh w trong V - S sao cho D[w] là nh nh t ; ấ ỉ ỏ ấ
Thêm w vào S ;
for m i đ nh u thu c V - S ỗ ỉ ộ do
D[u] := Min (D[u], D[w] + C[w, u]) ;
end;
end;
<!--[if !supportLineBreakNewLine]-->
<!--[endif]-->
N u mu n l u tr l i các đ nh trên đ ng đi ng n nh t đ có th xây d ng l i đ ng đi này t đ nhế ố ư ữ ạ ỉ ườ ắ ấ ể ể ự ạ ườ ừ ỉ
ngu n đ n các đ nh khác, ta dùng m t m ng P. M ng này s l u P[u] = w v i đ nh u là đ nh tr c c aồ ế ỉ ộ ả ả ẽ ư ớ ỉ ỉ ướ ủ
đ nh w trên đ ng đi ng n nh t. Lúc kh i đ u ta cho P[u] = 1, v i m i u khác 1. ỉ ườ ắ ấ ở ầ ớ ọ
Gi i thu t Dijkstra trên s đ c vi t l i nh sau : ả ậ ở ẽ ượ ế ạ ư
<!--[if !supportLineBreakNewLine]-->
<!--[endif]-->
procedure Dijkstra ;
begin
S := [1] ; { S ch ch a đ nh ngu n } ỉ ứ ỉ ồ
for i:=2 to n do
begin
D[i] := C[1, i] ; { Kh i đ u các giá tr cho D } ở ầ ị
P[i] := 1 ; { Kh i đ u các giá tr cho P } ở ầ ị
end ;
for i:=1 to n - 1 do
begin
L y đ nh w trong V - S sao cho D[w] là nh nh t ; ấ ỉ ỏ ấ
Thêm w vào S ;
for m i đ nh u thu c V - S ỗ ỉ ộ do
if (D[w] + C[w, u] < D [u]) then
begin
D[u] := D[w] + C[w, u] ; P[u] := w ;
end ;
end;
end;
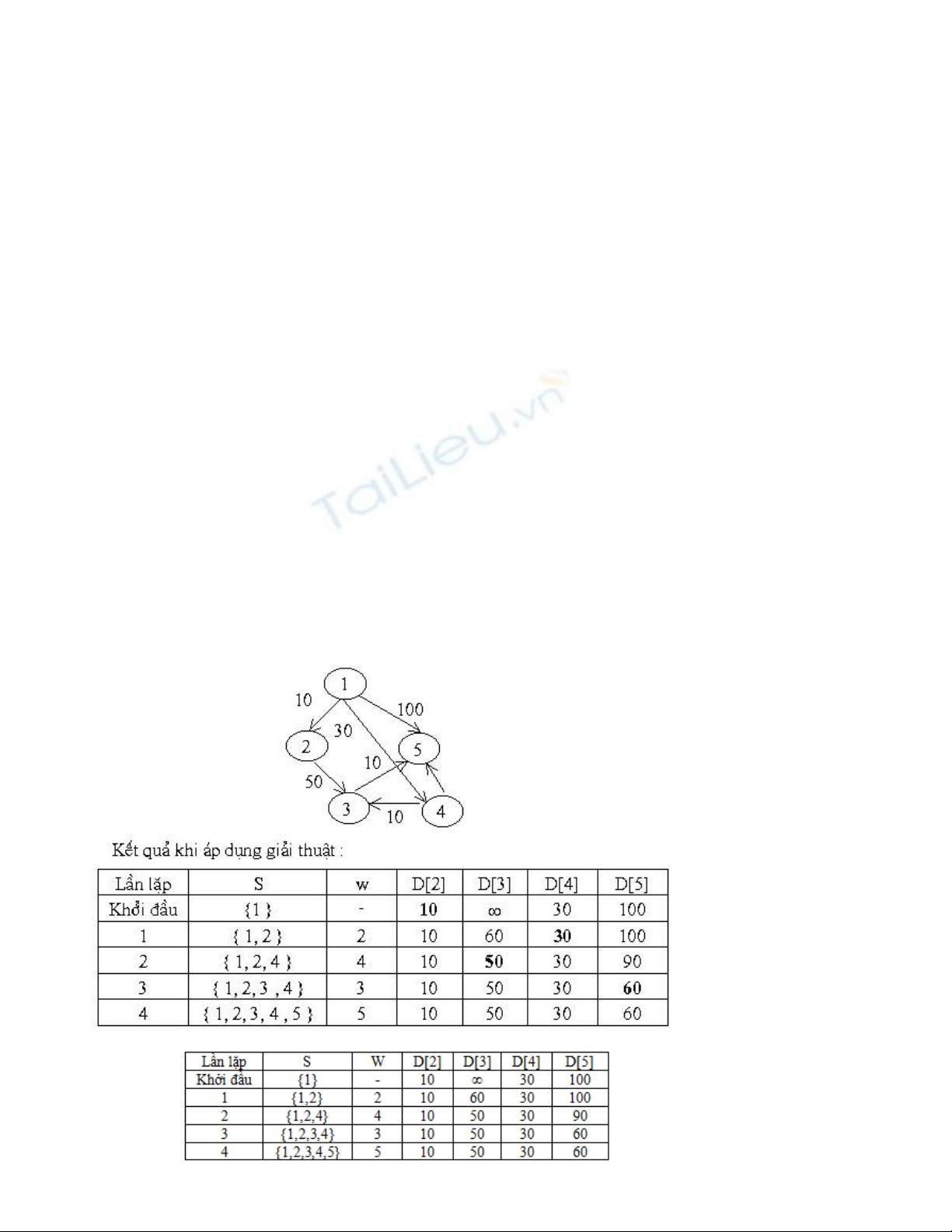
Ví d ụ: Áp d ng gi i thu t Dijkstra cho đ th hình sau: ụ ả ậ ồ ị
<!--[if !supportLineBreakNewLine]-->
procedure DijksTra;
begin
t:=false;
t[u0]:=true;
d[i]:=c[u0,i];{Neu khong co duong di thi d[i]=i’}
k:=1;{Da ket nap duoc 1 dinh}
while kdo
begin
{Tim min}
min:=i’;
for i:=1 to n do
if (d[i]<MIN)and(not t[i])then
begin
u:=i;
min:=d[u]
end;
t[u]:=true;{thêm u vao tập đỉnh}
inc(k);
{Tính lại đường đi}
for i:=1 to n do
if d[i]>d[u]+c[u,i] then
if not((d[i]=i’)and(d[u]=i’)and(c[u,i]=i’)) then
begin
d[i]:=d[u]+c[u,i];
truoc[i]:=u
end
end;
if d[v0]=i’ then
KhongCoDuongDi
else
QuayLaiMangTruocDeTimDuong
end;