T NG H P BÀI T P TOÁN C S (TH Y HOÀNG)Ổ Ợ Ậ Ơ Ở Ầ
CÂU H I TH O LU NỎ Ả Ậ
N i dungộTrang
Câu 1: Xây d ng m t mô hình hóa toán h c t m t n i dung th c ti nự ộ ọ ừ ộ ộ ự ễ
trong ch ng trình toán ph thông.ươ ổ 2
Câu 2: L y ví d v m r ng bài toán theo các con đng: Khái quát hóa,ấ ụ ề ở ộ ườ
T ng t hóa, đc bi t hóa, con đng khác.ươ ự ặ ệ ườ 10
Câu 3: So sánh h tiên đ Hilbert, h tiên đ Pogorelov, h tiên đ hìnhệ ề ệ ề ệ ề
h c ph thông.ọ ổ 22
Câu 4: H tiên đ ph thông đc th hi n nh th nào trong SGK phệ ề ổ ượ ể ệ ư ế ổ
thông. 30
Câu 5: Xác đnh và trình bày l i gi i c a các d ng toán 1, 2, 3 (trang 69)ị ờ ả ủ ạ
trong ph ng trình hàm.ươ 41
Câu 6: Phân tích c u trúc logic c a ch ng trình toán ph thông.ấ ủ ươ ổ 46
Câu 7: So sánh ch ng trình toán hi n hành v i ch ng trình toán sauươ ệ ớ ươ
2019. 58
Câu 8: Nêu nh ng sai l m v logic th ng g p h c sinh khi h c kháiữ ầ ề ườ ặ ở ọ ọ
ni m. Phân tích nguyên nhân nh ng sai l m này b ng logic toán.ệ ữ ầ ằ 66
Câu 9: Nêu nh ng sai l m v logic th ng g p h c sinh khi h c đnh lí.ữ ầ ề ườ ặ ở ọ ọ ị
Phân tích nguyên nhân nh ng sai l m này b ng logic toán.ữ ầ ằ 71
Câu 10: Nêu nh ng sai l m v logic th ng g p h c sinh khi gia bàiữ ầ ề ườ ặ ở ọ ỉ
t p toán. Phân tích nguyên nhân nh ng sai l m này b ng logic toán.ậ ữ ầ ằ 74
Câu 11: Dùng công th c c a đi s v t đ di n đt các đnh lí trong mônứ ủ ạ ố ị ừ ể ễ ạ ị
toán ph thông.ổ84
Câu 12: Xây D ng m t mô hình Toán h c theo quy trình 7 b c.ự ộ ọ ướ 86
1
Câu 13: C s đnh nghĩa phép nhân sô t nhiên qua phép c ng các sô ơ ơ ị ư ộ
h ng b ng nhau.ạ ằ 89
Câu 14: V n đ th c ti n đc ph n nh trong các ki n th c: C p s c ng, c p s ấ ề ự ễ ượ ả ả ế ứ ấ ố ộ ấ ố
nhân, hàm s , quan h t ng đng, quan h th t , quan h ánh x .ố ệ ươ ươ ệ ứ ự ệ ạ 90
Câu 15: V n d ng các phép suy lu n logic trong d y h c đnh líậ ụ ậ ạ ọ ị 95
Câu 16: Ch ng minh n u Q là t p đm đc thì QxQ là t p đm đcứ ế ậ ế ượ ậ ế ượ 104
Câu 17: Ch ng minh m t s đnh lý hình h c 10; 11; 12 d a trên tiên đ ứ ộ ố ị ọ ự ề
hình h c ph thông.ọ ổ 104
Câu 18: Quan đi m hàm s trong ch ng trình Toán ph thông? Th c ể ố ươ ổ ự
hi n d y h c m t n i dung c a ch ng trình Toán ph thông theo quan ệ ạ ọ ộ ộ ủ ươ ổ
đi m hàm s ?ể ố
105
Câu 19: C s logic c a ch ng trình toán 10;11;12. So sánh m c tiêu n i ơ ở ủ ươ ụ ộ
dung ch ng trình hi n hành v i ch ng trình m i sau 2019.ươ ệ ớ ươ ớ 110
Câu 20: Ch ng minh m t s đnh lý gi i tích 11, 12 theo ngôn ng không ứ ộ ố ị ả ữ
gian topo, không gian metric và ngôn ng toán ph thông?ữ ổ 117
2
Câu 1. Xây d ng m t mô hình hóa toán h c t m t n i dung th c ti n trong ch ng ự ộ ọ ừ ộ ộ ự ễ ươ
trình toán ph thông.ổ
Nhóm 1
B c 1ướ : V n đ th c ti n. ấ ề ự ễ
Nhân d p m ng xuân M u tu t 2018, nhi u qu n (huy n) c a các t nh thành đu ị ừ ậ ấ ề ậ ệ ủ ỉ ề
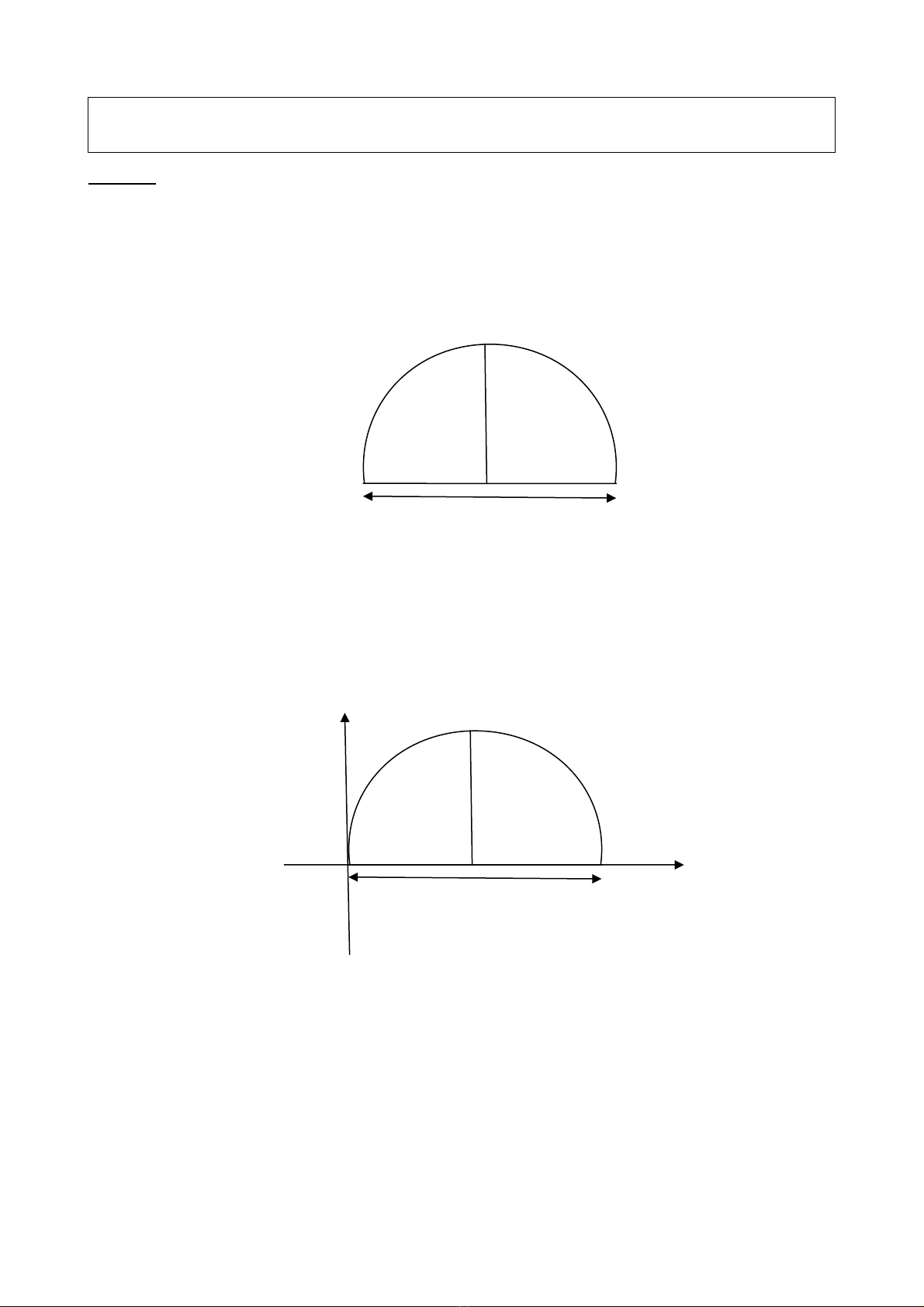
có trang trí m t cái c ng đ m ng năm m i. m t huy n X, thi t k m t cái c ng nh ộ ổ ể ừ ớ Ở ộ ệ ế ế ộ ổ ư
hình v sau v i chi u r ng là 8m, chi u cao là 3,5m. Xác đnh đng cong thi t k c ng ẽ ớ ề ộ ề ị ườ ế ế ổ
và tính di n tích ph n xe đi qua gi i h n b i c ng và m t đt.ệ ầ ớ ạ ở ổ ặ ấ
B c 2ướ : L p gi thuy t.ậ ả ế
Các tham s xu t hi n trong bài toán là chi u r ng, chi u cao c a c ng và đng ố ấ ệ ề ộ ề ủ ổ ườ
cong có d ng hình parabol.ạ
B c 3ướ : Xây d ng bài toán. ự
Trong măt ph ng Oxy, Ch n O(0; 0), A(4; 3,5), B(8; 0) nh hình vẳ ọ ư ẽ
a. Xác đnh parabol (P): y = axị2 + bx + c đi qua O, A, B.
b. Tính di n tích hình ph ng gi i h n b i đ th hàm s (P), tr c hoành và 2 đngệ ẳ ớ ạ ở ồ ị ố ụ ườ
th ng x = 0, x = 8.ẳ
B c 4ướ : Gi i bài toán.ả
a. Vì (P) đi qua O, A, B nên ta có h ph ng trình.ệ ươ
3
8m
3,5m
A
A
O
y
x
8m
3,5m
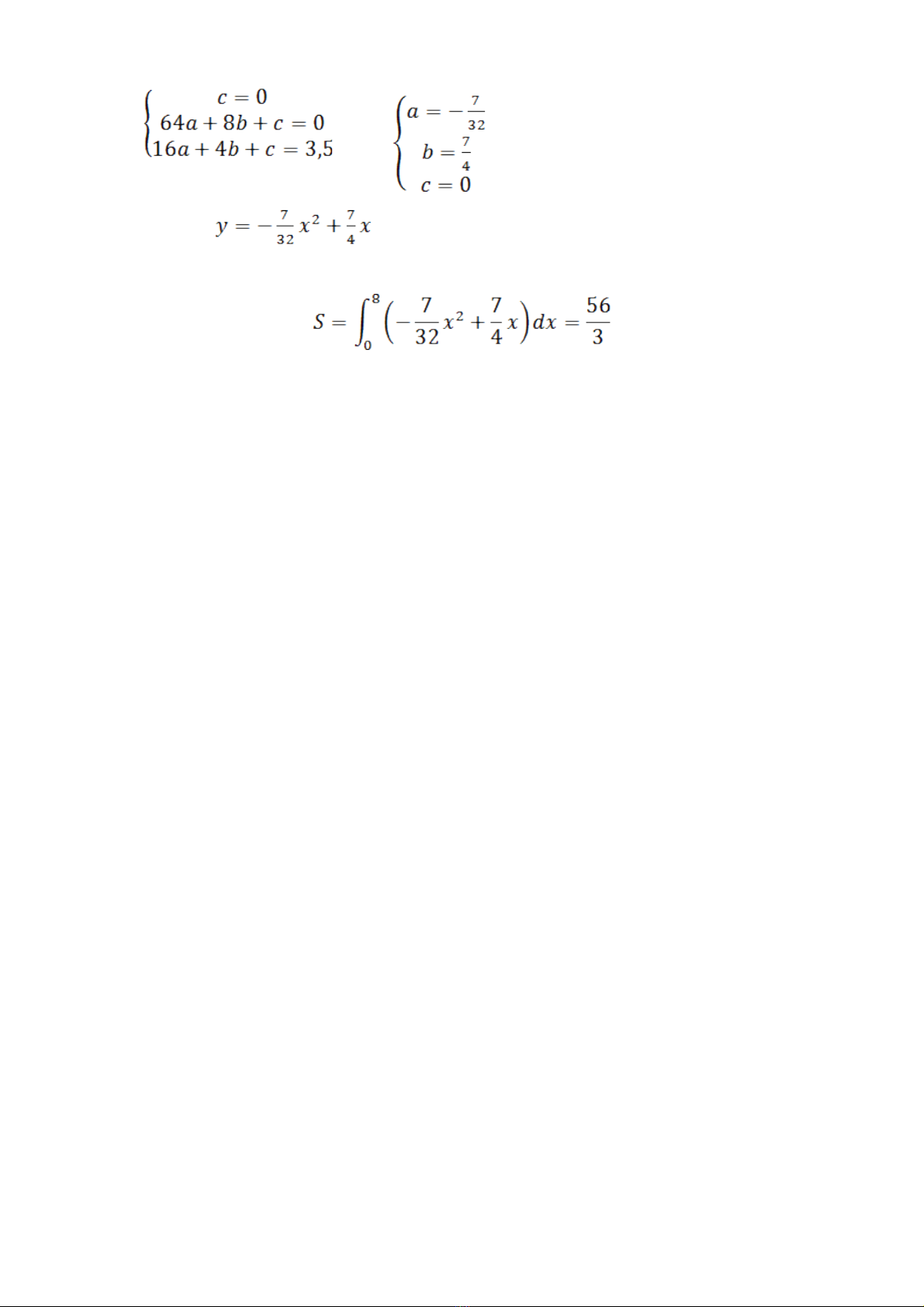
V y (P) ậ
b. Di n tích hình ph ng c n tìm làệ ẳ ầ
B c 5ướ : Hi u l i gi i bài toán.ể ờ ả
Đ tính đc di n tích hình ph ng gi i h n, ta c n xác đnh đc đng cong có ể ượ ệ ẳ ớ ạ ầ ị ượ ườ
d ng hình parabol, đ xác đnh đc đng cong parabol ta c n ch n h tr c t a đ phù ạ ể ị ượ ườ ầ ọ ệ ụ ọ ộ
h p.ợ
B c 6ướ : Ki m nghi m mô hình.ể ệ
Th c t vi c thi t k có d ng đng cong ng d ng r t nhi u trong th c t và ự ế ệ ế ế ạ ườ ứ ụ ấ ề ự ế
ch n s li u phù h p đ ít t n chi phí.ọ ố ệ ợ ể ố
B c 7ướ : Thông báo, gi i thích, d đoán.ả ự
4
Nhóm 2
Vi c v n d ng ki n th c toán h c vào gi i quy t các v n đ th c ti n và ng cệ ậ ụ ế ứ ọ ả ế ấ ề ự ễ ượ
l i là m t v n đ quan tr ng trong d y và h c toán tr ng ph thông. Đi u này giúpạ ộ ấ ề ọ ạ ọ ở ườ ổ ề
h c sinh càng say mê h c toán t đó k t qu c a vi c gi ng d y s thu đc nhi u k tọ ọ ừ ế ả ủ ệ ả ạ ẽ ượ ề ế
qu mong mu n. Do đó, m t v n đ đc đt ra là d y h c toán nên quan tâm nh ng víả ố ộ ấ ề ượ ặ ạ ọ ữ
d xu t phát t th c t giúp h c sinh th y đc m i liên h gi a toán h c và cu c s ngụ ấ ừ ự ế ọ ấ ượ ố ệ ữ ọ ộ ố
th ng ngày. Mô hình hóa toán h c cho phép h c sinh k t n i toán h c v i th gi i th c.ườ ọ ọ ế ố ọ ớ ế ớ ự
Ví dụ: a/ Th c tự ế : Tính chi u cao c ng d ng Parabol.ề ổ ạ
b/ Toán h cọ : Xác đnh Parabol ị
0
2
acbxaxy
bi t Parabol đi qua 3 đi m.ế ể
B c 1ướ : Tìm hi u v n đ th c ti n.ể ấ ề ự ễ
R t nhi u công trình ki n trúc, bi u t ng Vi t Nam nói riêng và trên c thấ ề ế ể ượ ở ệ ả ế
gi i đc thi t k d ng hình Parabol.ớ ượ ế ế ạ
V n đ đt ra là làm th nào đ đo đc chi u cao c ng Acx khi không đo đcấ ề ặ ế ể ượ ề ổ ơ ạ
tr c ti p, vì c ng cao s gây nguy hi m khi đo đc.ự ế ổ ẽ ể ạ
B c 2ướ : L p gi thuy t.ậ ả ế
-Đo đc kho ng cách c a 2 tr c ng.ạ ả ủ ụ ổ
- Tìm 3 đi m n m trên c ng và có t a đ (các đ dài đo đc)ể ằ ổ ọ ộ ộ ượ
B c 3ướ : Xây d ng bài toán.ự
Bài toán trên th c t chúng ta g n hình nh c ng Acx đó vào m t ph ng trìnhự ế ắ ả ổ ơ ộ ươ
c a hàm s b c hai d ng ủ ố ậ ạ
0
2
acbxaxy
và t đó s tìm đc t a đ đnh c aừ ẽ ượ ọ ộ ỉ ủ
Parabol là
.
4
;
2
aa
b
S
B c 4ướ : Gi i bài toán.ả
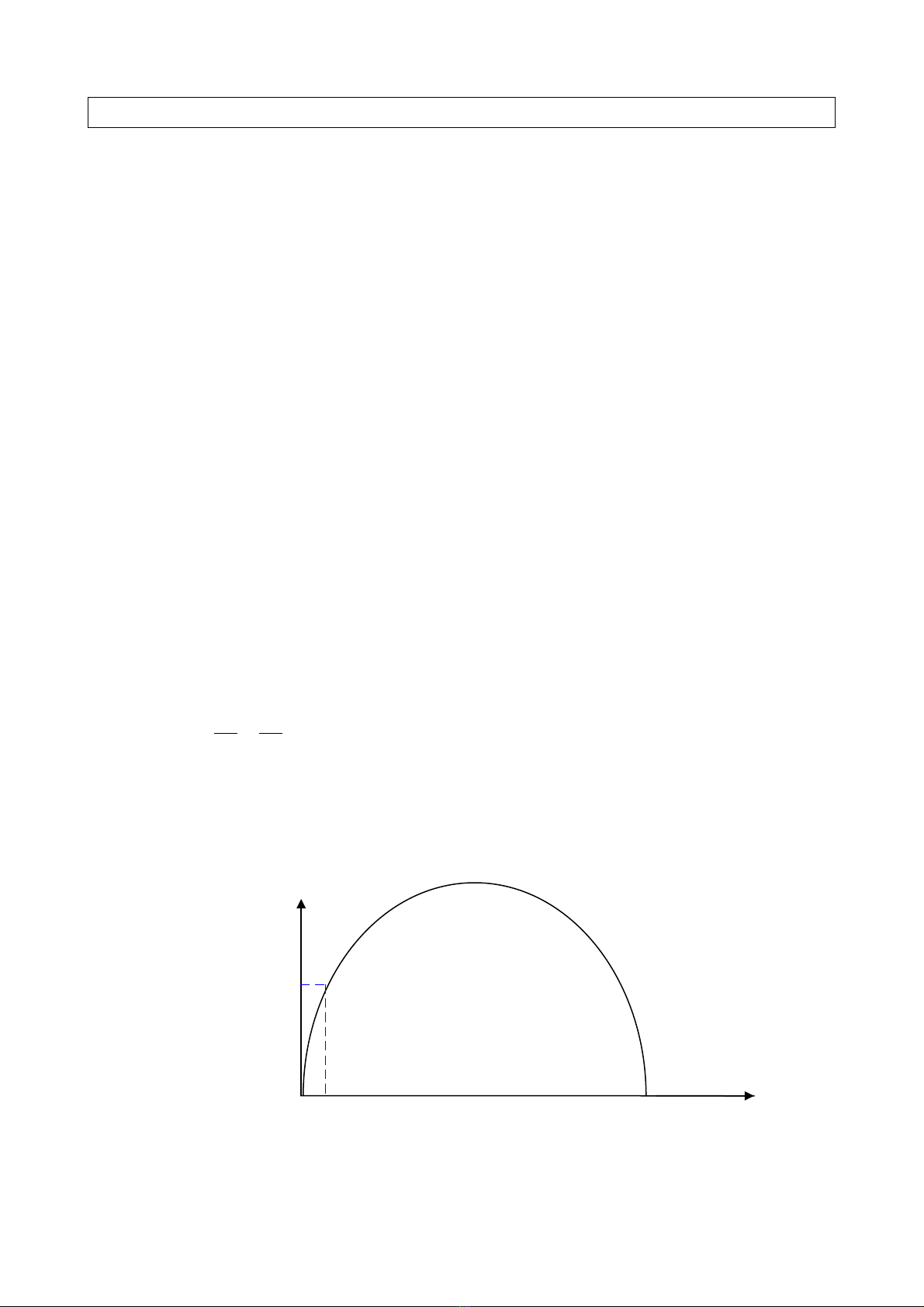
Đn gi n v n đ : Ch n h tr c t a đ ơ ả ấ ề ọ ệ ụ ọ ộ
xy0
sao cho g c t a đ 0 trùng m t chânố ọ ộ ộ
c a c ng (nh hình v )ủ ổ ư ẽ
5
O
M
Bx
y