12
+ Cấu trúc SISO là cấu trúc trong đó luật hợp thành có các mệnh đề
điều kiện và mệnh đề kết luận là các mệnh đề đơn.
Ví dụ: R1: nếu χ = Al thì γ = B1 hoặc
R2: nếu χ = A2 thì γ = B2.
+ Cấu trúc MISO là cấu trúc trong đó luật hợp thành có các mệnh đề
điều kiện là mệnh đề phức và mệnh đề kết luận là mệnh đề đơn.
Ví dụ: R1: nếu χ1 = A1 và χ2 = B1 thì γ = C1 hoặc
R2: nếu χ1 = A2 và χ2 = B2 thì γ = C2.
1.5.5. Luật hợp thành đơn có cấu trúc SISO
a) Luật hợp thành MIN
Luật hợp thành MIN là tên gọi mô hình (ma trận) R của mệnh đề hợp
thành A⇒B khi hàm liên thuộc µA=>B(x, y) của nó được xây dựng theo quy
tắc MIN.
Xét luật hợp thành chỉ có 1 mệnh đề: Nếu χ = A thì γ = B
Để xây dựng R, trước tiên hai hàm liên thuộc µA(x) và µB(y) được rời rạc
hoá với tần số rời rạc đủ nhỏ để không bị mất thông tin.
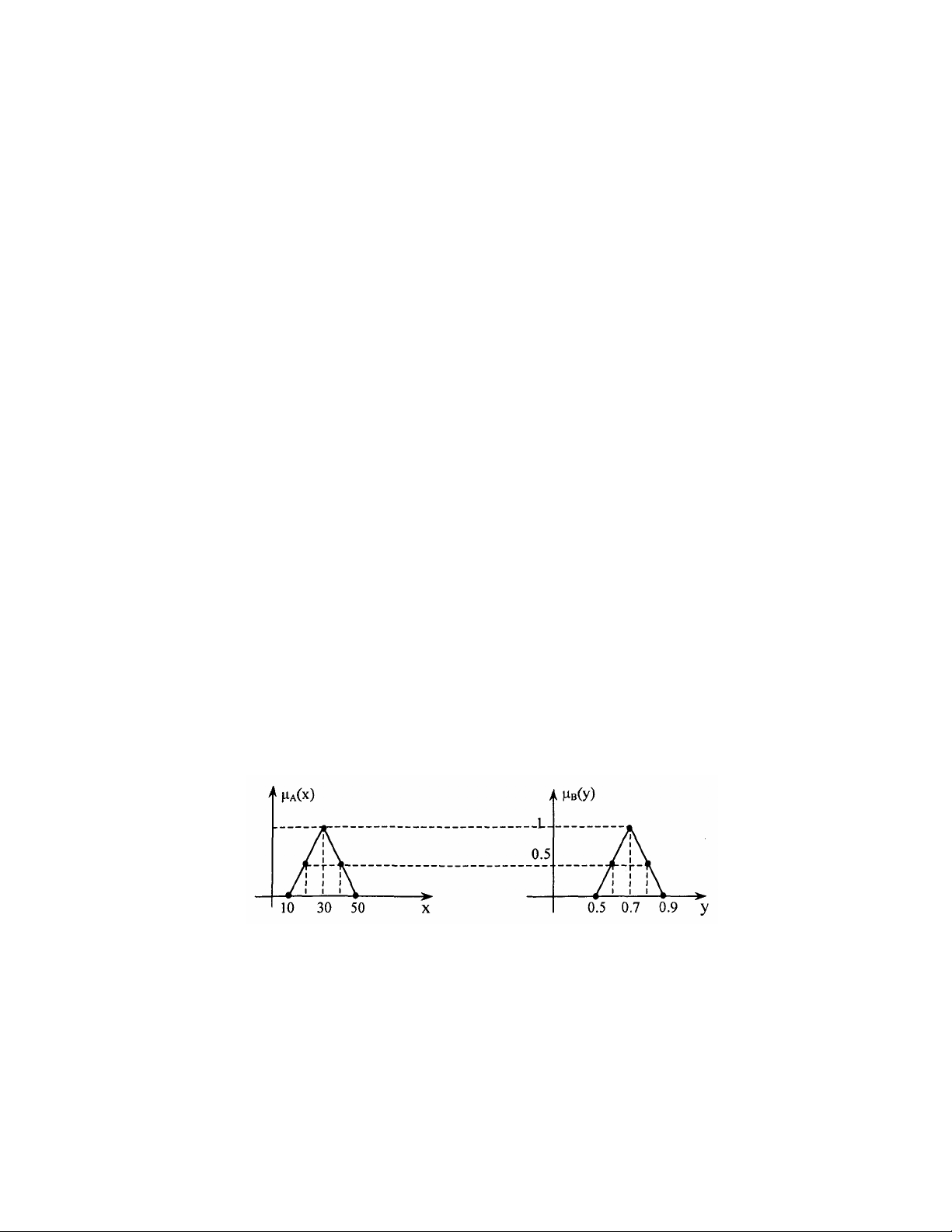
Ví dụ: µA(x), µB(y) được rời rạc hoá tại các điểm:
x ∈{10, 20, 30, 40, 50}
y ∈{0.5, 0.6, 0.7, 0.8, 0.9}.
Với các điểm rời rạc này thì theo
µA=>B(20; 0.7) = µR(20; 0.7)=MIN{µA(20),µb(0.7)}=MIN{0.5; 1}= 0.5
µA=>B(30; 0.7) = µR(30; 0.7)=MIN{µA(30),µb(0.7)}= MIN{1; 1}= 1
……………………….
Hình 1.10. Rời rạc hoá các hàm liên thuộc
13
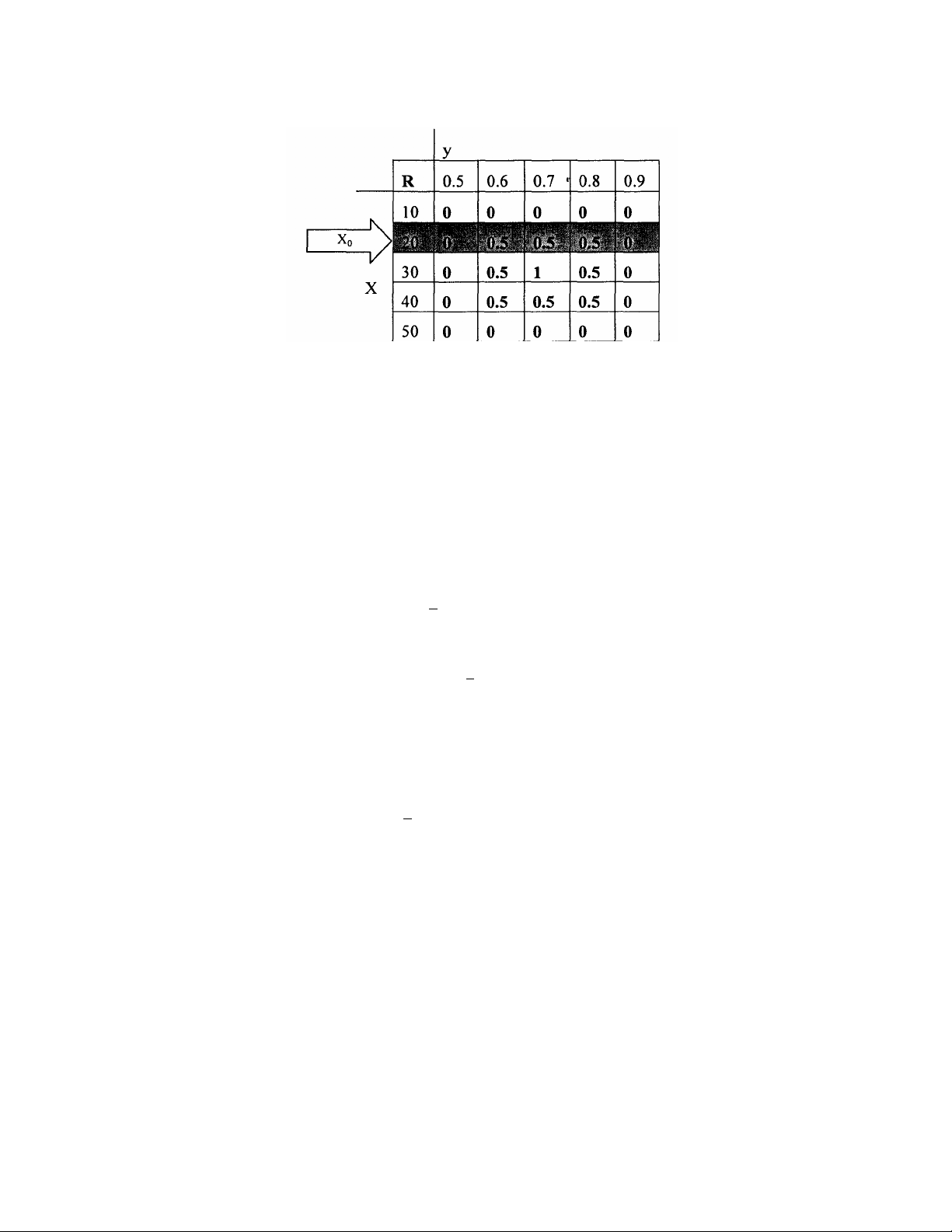
Nhóm tất cả các giá trị µA=>B(x, y) = µR(x,y) gồm 5 x 5= 25 giá trị, thành
ma trận R (được gọi là ma trận hợp thành MIN) gồm 5 hàng 5 cột.
Khi tín hiệu đầu vào là một giá trị rõ x0 = 20, tín hiệu đầu ra B’ có hàm
liên thuộc:
µB’(y) = µR(20, y) = {0; 0.5; 0.5; 0.5; 0}.
Để thuận tiện cho việc xác định hàm liên thuộc của tín hiệu ra dưới dạng
nhân ma trận, ta định nghĩa một ma trận T = {a1 a2…} ma trận này chỉ có một
phần tử bằng 1 còn các phần tử khác đều bằng 0. Ví dụ với tập 5 phần tử cho
tín hiệu đầu vào xử {10; 20; 30; 40; 50} thì ứng với x0 = 20 (phần tử thứ hai)
ta có:
a = (0 1 0 0 0)
Và khi đó
µB’(y) = µR(x0, y) = aT. R = {0 0.5 0.5 0.5 0}.
Tổng quát cho một giá trị rõ x0 bất kỳ
x0
∈
X = {10 20 30 40 50}
tại đầu vào véctơ chuyển vị có dạng:
aT = (a1, a2, a3, a4, a5)
trong đó chỉ có một phần tử a; duy nhất có chỉ số i là chỉ số của x0 trong X có
giá trị bằng 1, các phần tử còn lại đều bằng 0. Hàm liên thuộc mB'(y) dưới
dạng rời rạc được xác định:
14
Chú ý: Trong biểu thức (1.1) để tính µB'(y) ta cần cài đặt thuật toán nhân
ma trận của đại số tuyến tính, do đó tốc độ xử lý chậm. Để khắc phục nhược
điểm này, phép nhân ma trận (1.1) được thay bởi luật MAX-MIN của Zadeh
với MAX (phép lấy cực đại) thay vào vị trí phép cộng và MIN (phép lấy cực
tiểu) thay vào vị trí phép nhân. Khi đó:
lK = 51
max
≤≤imin {ai rki}
Kết quả hai phép tính (1.1) và (1.2) với đầu vào là một giá trị rõ hoàn
toàn giống nhau. Cũng từ lý do trên mà luật hợp thành MIN còn có tên gọi là
luật hợp thành MAX-MIN.
b/ Luật hợp thành PROD
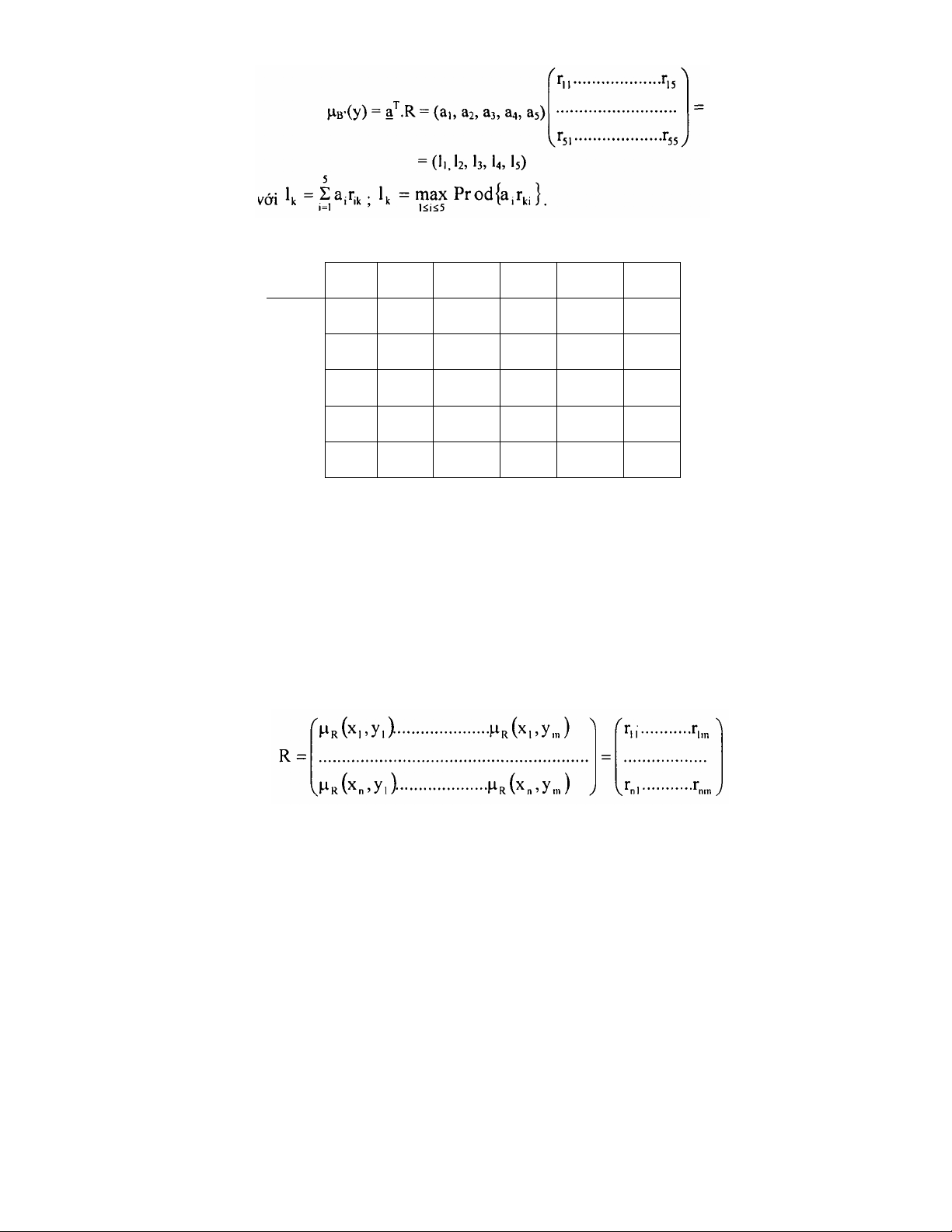
Tương tự như đã làm với luật hợp thành MIN, ma trận R của luật hợp
thành PROD được xây dựng gồm các hàng là m giá trị rời rạc của đầu ra
µB'(y1), µB'(y2), µB'(ym) cho n giá trị rõ đầu vào xn, xn,…., xn Như Vậy ma trận
R sẽ có n hàng và m cột. Xét ví dụ trên cho 5 giá trị đầu vào:
{x1, x2, x3, x4, x5} = {10 20 30 40 50}
thì với từng giá trị xi, 5 giá trị của hàm liên thuộc đầu ra tương ứng µB'(0.5),
µB'(0.6), µB'(0.7), µB'(0.8), µB'(0.9) được liệt kê trong ma trận R được gọi là
ma trận hợp thành PROD.
Từ ma trận R trên, hàm liên thuộc µB'(y) của giá trị đầu ra khi đầu vào là
giá trị rõ x4 cũng được xác định bằng công thức:
aT = (0, 0, 0, 1, 0)
µB'(y) = µR(x4, y) = aT .R = {0, 0.25, 0.5, 0.25, 0}.
Đê rút ngắn thời gian tính và cũng để mở rộng công thức trên cho trường
hợp đầu vào là giá trị mờ, phép nhân ma trận T.R cũng được thay bằng luật
MAX- PROD của Zadeh như đã làm cho luật hợp thành MIN. Trong đó phép
nhân được thực hiện bình thường còn phép lấy cực đại thay vào vị trí của
phép cộng.
15
R 0.5 0.6 0.7 0.8 0.9
i = 1 10 0 0 0 0 0
i = 2 20 0 0.25 0.5 0.25 0
i = 3 30 0 0.5 1 0.5 0
i = 4 40 0 0.25 0.5 0.25 0
i = 5 50 0 0 0 0 0
c) Thuật toán xây dựng R
Từ các phân tích trên, ta rút ra thuật toán xây dựng R cho luật hợp thành
đơn có cấu trúc SISO (Nếu χ = A Thì γ = B) như sau:
1- Rời rạc hoá µA(x) tại n điểm x1, x2,…,xn tại m điểm y1, y2,…,yn (n có
thể khác m)
2- Xây dựng ma trận R gồm n hàng và m cột:
3- Xác định hàm liên thuộc µB'(y) của đầu ra ứng với giá trị rõ dầu vào xk
theo biểu thức:
16
trong đó: lK = ni≤≤1
max min {ai r
ki}, k = 1,2,.., m nếu sử dụng công thức
MAX-MIN và lK = ni≤≤1
max prod {ai r
ki}, k = 1,2,.., m nếu sử dụng công thức
MAX-PROD.
4- Xác định µB'(y) theo công thức: µB'(y) = ( l1, l2,…,lm).
Chú ý:
Trong trường hợp đầu vào là giá trị mờ A' với hàm liên thuộc µA'(y)
thì hàm liên thuộc µB'(y) của giá trị đầu ra B': µB'(y) = ( l1, l2,…,lm) cũng được
tính theo công thức (2.4) và
lk = ni≤≤1
max min {ai rki}, k = 1, 2,…, m
trong đó a là véctơ gồm các giá trị rời rạc của hàm liên thuộc µA'(x) của
A' tại các điểm:
x ∈ X = {x1, x2,…,xn} tức là aT = (µA'(x1), µA'(x2),…, µA'(xn)).
Giả thiết có n điểm rời rạc x1, x2,…,xn của cơ sở A và m điểm rời rạc
y1, y2,…,ym của cơ sở B ta có hai véctơ:
µAT={µA(x1), µA(x2),…, µA(xn)} và µAT={µB(y1), µB(y2),…, µB(xm)}
theo Zadeh ta có thể xác đinh ngay được R thông qua tích dyadic, tức là tích
của một véctơ với một véctơ chuyển vị:
R = µA.µBT
Trong đó nếu quy tắc áp dụng là MAX - MIN thì phép nhân phải được
thay bằng phép tính lấy cực tiểu (min), với quy tắc MAX - PROD thì thực
hiện phép nhân như bình thường.
Ví dụ: Luật điều khiển: Nếu χ = A Thì γ = B. Hãy xây dựng ma trận R
của luật µA⇒B(x, y).