* * * 101
circumscribed circle of triangle ADE is equal to the distance between the centers of the
inscribed and circumscribed circles of triangle ABC.
§2. Right triangles
5.15. In triangle ABC, angle ∠Cis a right one. Prove that r=a+b−c
2and rc=a+b+c
2.
5.16. In triangle ABC, let Mbe the midpoint of side AB. Prove that CM =1
2AB if
and only if ∠ACB = 90◦.
5.17. Consider trapezoid ABCD with base AD. The bisectors of the outer angles at
vertices Aand Bmeet at point Pand the bisectors of the angles at vertices Cand Dmeet at
point Q. Prove that the length of segment P Q is equal to a half perimeter of the trapezoid.
5.18. In an isosceles triangle ABC with base AC bisector CD is drawn. The line
that passes through point Dperpendicularly to DC intersects AC at point E. Prove that
EC = 2AD.
5.19. The sum of angles at the base of a trapezoid is equal to 90◦. Prove that the
segment that connects the midpoints of the bases is equal to a half difference of the bases.
5.20. In a right triangle ABC, height CK from the vertex Cof the right angle is drawn
and in triangle ACK bisector CE is drawn. Prove that CB =BE.
5.21. In a right triangle ABC with right angle ∠C, height CD and bisector CF are
drawn; let DK and DL be bisectors in triangles BDC and ADC. Prove that CLF K is a
square.
5.22. On hypothenuse AB of right triangle ABC, square ABP Q is constructed outwards.
Let α=∠ACQ,β=∠QCP and γ=∠P CB. Prove that cos β= cos α·cos γ.
See also Problems 2.65, 5.62.
§3. The equilateral triangles
5.23. From a point Minside an equilateral triangle ABC perpendiculars M P ,MQ and
MR are dropped to sides AB,BC and CA, respectively. Prove that
AP 2+BQ2+CR2=P B2+QC2+RA2,
AP +BQ +CR =P B +QC +RA.
5.24. Points Dand Edivide sides AC and AB of an equilateral triangle ABC in the
ratio of AD :DC =BE :EA = 1 : 2. Lines BD and CE meet at point O. Prove that
∠AOC = 90◦.
***
5.25. A circle divides each of the sides of a triangle into three equal parts. Prove that
this triangle is an equilateral one.
5.26. Prove that if the intersection point of the heights of an acute triangle divides the
heights in the same ratio, then the triangle is an equilateral one.
5.27. a) Prove that if a+ha=b+hb=c+hc, then triangle ABC is a equilateral one.
b) Three squares are inscribed in triangle ABC: two vertices of one of the squares lie on
side AC, those of another one lie on side BC, and those of the third lie one on AB. Prove
that if all the three squares are equal, then triangle ABC is an equilateral one.
5.28. The circle inscribed in triangle ABC is tangent to the sides of the triangle at
points A1,B1,C1. Prove that if triangles ABC and A1B1C1are similar, then triangle ABC
is an equilateral one.
5.29. The radius of the inscribed circle of a triangle is equal to 1, the lengths of the
heights of the triangle are integers. Prove that the triangle is an equilateral one.
102 CHAPTER 5. TRIANGLES
See also Problems 2.18, 2.26, 2.36, 2.44, 2.54, 4.46, 5.56, 7.45, 10.3, 10.77, 11.3, 11.5,
16.7, 18.9, 18.12, 18.15, 18.17-18.20, 18.22, 18.38, 24.1.
§4. Triangles with angles of 60◦and 120◦
5.30. In triangle ABC with angle Aequal to 120◦bisectors AA1,BB1and CC1are
drawn. Prove that triangle A1B1C1is a right one.
5.31. In triangle ABC with angle Aequal to 120◦bisectors AA1,BB1and CC1meet
at point O. Prove that ∠A1C1O= 30◦.
5.32. a) Prove that if angle ∠Aof triangle ABC is equal to 120◦then the center of the
circumscribed circle and the orthocenter are symmetric through the bisector of the outer
angle ∠A.
b) In triangle ABC, the angle ∠Ais equal to 60◦;Ois the center of the circumscribed
circle, His the orthocenter, Iis the center of the inscribed circle and Iais the center of the
escribed circle tangent to side BC. Prove that IO =IH and IaO=IaH.
5.33. In triangle ABC angle ∠Ais equal to 120◦. Prove that from segments of lengths
a,band b+ca triangle can be formed.
5.34. In an acute triangle ABC with angle ∠Aequal to 60◦the heights meet at point
H.
a) Let Mand Nbe the intersection points of the midperpendiculars to segments BH
and CH with sides AB and AC, respectively. Prove that points M,Nand Hlie on one
line.
b) Prove that the center Oof the circumscribed circle lies on the same line.
5.35. In triangle ABC, bisectors BB1and CC1are drawn. Prove that if ∠CC1B1= 30◦,
then either ∠A= 60◦or ∠B= 120◦.
See also Problem 2.33.
§5. Integer triangles
5.36. The lengths of the sides of a triangle are consecutive integers. Find these integers
if it is known that one of the medians is perpendicular to one of the bisectors.
5.37. The lengths of all the sides of a right triangle are integers and the greatest common
divisor of these integers is equal to 1. Prove that the legs of the triangle are equal to 2mn
and m2−n2and the hypothenuse is equal to m2+n2, where mand nare integers.
A right triangle the lengths of whose sides are integers is called a Pythagorean triangle.
5.38. The radius of the inscribed circle of a triangle is equal to 1 and the lengths of its
sides are integers. Prove that these integers are equal to 3, 4, 5.
5.39. Give an example of an inscribed quadrilateral with pairwise distinct integer lengths
of sides and the lengths of whose diagonals, the area and the radius of the circumscribed
circle are all integers. (Brakhmagupta.)
5.40. a) Indicate two right triangles from which one can compose a triangle so that the
lengths of the sides and the area of the composed triangle would be integers.
b) Prove that if the area of a triangle is an integer and the lengths of the sides are
consecutive integers then this triangle can be composed of two right triangles the lengths of
whose sides are integers.
5.41. a) In triangle ABC, the lengths of whose sides are rational numbers, height BB1
is drawn.
Prove that the lengths of segments AB1and CB1are rational numbers.
§6. MISCELLANEOUS PROBLEMS 103
b) The lengths of the sides and diagonals of a convex quadrilateral are rational numbers.
Prove that the diagonals cut it into four triangles the lengths of whose sides are rational
numbers.
See also Problem 26.7.
§6. Miscellaneous problems
5.42. Triangles ABC and A1B1C1are such that either their corresponding angles are
equal or their sum is equal to 180◦. Prove that the corresponding angles are equal, actually.
5.43. Inside triangle ABC an arbitrary point Ois taken. Let points A1,B1and C1be
symmetric to Othrough the midpoints of sides BC,CA and AB, respectively. Prove that
△ABC =△A1B1C1and, moreover, lines AA1,BB1and CC1meet at one point.
5.44. Through the intersection point Oof the bisectors of triangle ABC lines parallel
to the sides of the triangle are drawn. The line parallel to AB meets AC and BC at points
Mand N, respectively, and lines parallel to AC and BC meet AB at points Pand Q,
respectively. Prove that M N =AM +BN and the perimeter of triangle OP Q is equal to
the length of segment AB.
5.45. a) Prove that the heigths of a triangle meet at one point.
b) Let Hbe the intersection point of heights of triangle ABC and Rthe radius of the
circumscribed circle. Prove that
AH2+BC2= 4R2and AH =BC|cot α|.
5.46. Let x= sin 18◦. Prove that 4x2+ 2x= 1.
5.47. Prove that the projections of vertex Aof triangle ABC on the bisectors of the
outer and inner angles at vertices Band Clie on one line.
5.48. Prove that if two bisectors in a triangle are equal, then the triangle is an isosceles
one.
5.49. a) In triangles ABC and A′B′C′, sides AC and A′C′are equal, the angles at
vertices Band B′are equal, and the bisectors of angles ∠Band ∠B′are equal. Prove that
these triangles are equal. (More precisely, either △ABC =△A′B′C′or △ABC =△C′B′A′.)
b) Through point Don the bisector BB1of angle ABC lines AA1and CC1are drawn
(points A1and C1lie on sides of triangle ABC). Prove that if AA1=CC1, then AB =BC.
5.50. Prove that a line divides the perimeter and the area of a triangle in equal ratios if
and only if it passes through the center of the inscribed circle.
5.51. Point Eis the midpoint of arc ⌣ AB of the circumscribed circle of triangle ABC
on which point Clies; let C1be the midpoint of side AB. Perpendicular EF is dropped
from point Eto AC. Prove that:
a) line C1Fdivides the perimeter of triangle ABC in halves;
b) three such lines constructed for each side of the triangle meet at one point.
5.52. On sides AB and BC of an acute triangle ABC, squares ABC1D1and A2BCD2
are constructed outwards. Prove that the intersection point of lines AD2and CD1lies on
height BH.
5.53. On sides of triangle ABC squares centered at A1,B1and C1are constructed
outwards. Let a1,b1and c1be the lengths of the sides of triangle A1B1C1; let Sand S1be
the areas of triangles ABC and A1B1C1, respectively. Prove that:
a) a2
1+b2
1+c2
1=a2+b2+c2+ 6S.
b) S1−S=1
8(a2+b2+c2).
5.54. On sides AB,BC and CA of triangle ABC (or on their extensions), points C1,
A1and B1, respectively, are taken so that ∠(CC1, AB) = ∠(AA1, BC) = ∠(BB1, CA) =
104 CHAPTER 5. TRIANGLES
α. Lines AA1and BB1,BB1and CC1,CC1and AA1intersect at points C′,A′and B′,
respectively. Prove that:
a) the intersection point of heights of triangle ABC coincides with the center of the
circumscribed circle of triangle A′B′C′;
b) △A′B′C′∼ △ABC and the similarity coefficient is equal to 2 cos α.
5.55. On sides of triangle ABC points A1,B1and C1are taken so that AB1:B1C=
cn:an,BC1:CA =an:bnand CA1:A1B=bn:cn(here a,band care the lengths of
the triangle’s sides). The circumscribed circle of triangle A1B1C1singles out on the sides of
triangle ABC segments of length ±x, ±yand ±z, where the signs are chosen in accordance
with the orientation of the triangle. Prove that
x
an−1+y
bn−1+z
cn−1= 0.
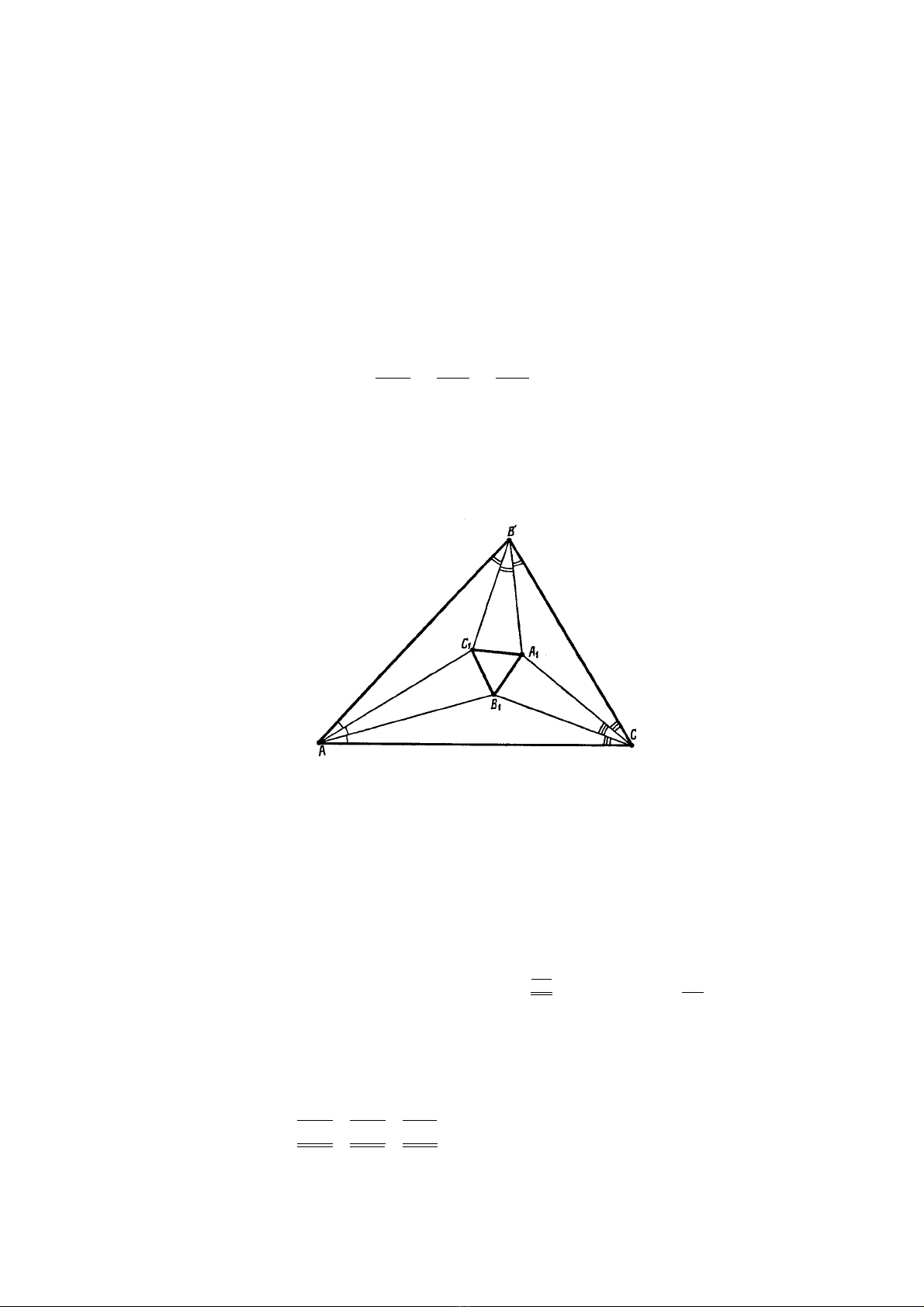
5.56. In triangle ABC trisectors (the rays that divide the angles into three equal parts)
are drawn. The nearest to side BC trisectors of angles Band Cintersect at point A1; let us
define points B1and C1similarly, (Fig. 55). Prove that triangle A1B1C1is an equilateral
one. (Morlie’s theorem.)
Figure 55 (5.56)
5.57. On the sides of an equilateral triangle ABC as on bases, isosceles triangles A1BC,
AB1Cand ABC1with angles α,βand γat the bases such that α+β+γ= 60◦are
constructed inwards. Lines BC1and B1Cmeet at point A2, lines AC1and A1Cmeet at
point B2, and lines AB1and A1Bmeet at point C2. Prove that the angles of triangle A2B2C2
are equal to 3α, 3βand 3γ.
§7. Menelaus’s theorem
Let −→
AB and −−→
CD be colinear vectors. Denote by AB
CD the quantity ±AB
CD , where the plus
sign is taken if the vectors −→
AB and −−→
CD are codirected and the minus sign if the vectors are
directed opposite to each other.
5.58. On sides BC,CA and AB of triangle ABC (or on their extensions) points A1,B1
and C1, respectively, are taken. Prove that points A1,B1and C1lie on one line if and only
if
BA1
CA1·CB1
AB1·AC1
BC1
= 1.(Menelaus’s theorem)
5.59. Prove Problem 5.85 a) with the help of Menelaus’s theorem.
* * * 105
5.60. A circle Sis tangent to circles S1and S2at points A1and A2, respectively. Prove
that line A1A2passes through the intersection point of either common outer or common
inner tangents to circles S1and S2.
5.61. a) The midperpendicular to the bisector AD of triangle ABC intersects line BC
at point E. Prove that BE :CE =c2:b2.
b) Prove that the intersection point of the midperpendiculars to the bisectors of a triangle
and the extensions of the corresponding sides lie on one line.
5.62. From vertex Cof the right angle of triangle ABC height CK is dropped and in
triangle ACK bisector CE is drawn. Line that passes through point Bparallel to CE meets
CK at point F. Prove that line EF divides segment AC in halves.
5.63. On lines BC,CA and AB points A1,B1and C1, respectively, are taken so that
points A1,B1and C1lie on one line. The lines symmetric to lines AA1,BB1and CC1
through the corresponding bisectors of triangle ABC meet lines BC,CA and AB at points
A2,B2and C2, respectively. Prove that points A2,B2and C2lie on one line.
***
5.64. Lines AA1,BB1and CC1meet at one point, O. Prove that the intersection points
of lines AB and A1B1,BC and B1C1,AC and A1C1lie on one line. (Desargues’s theorem.)
5.65. Points A1,B1and C1are taken on one line and points A2,B2and C2are taken on
another line. The intersection pointa of lines A1B2with A2B1,B1C2with B2C1and C1A2
with C2A1are C,Aand B, respectively. Prove that points A,Band Clie on one line.
(Pappus’ theorem.)
5.66. On sides AB,BC and CD of quadrilateral ABCD (or on their extensions) points
K,Land Mare taken. Lines KL and AC meet at point P, lines LM and BD meet at
point Q. Prove that the intersection point of lines KQ and M P lies on line AD.
5.67. The extensions of sides AB and CD of quadrilateral ABCD meet at point Pand
the extensions of sides BC and AD meet at point Q. Through point Pa line is drawn that
intersects sides BC and AD at points Eand F. Prove that the intersection points of the
diagonals of quadrilaterals ABCD,ABEF and CDF E lie on the line that passes through
point Q.
5.68. a) Through points Pand Qtriples of lines are drawn. Let us denote their
intersection points as shown on Fig. 56. Prove that lines KL,AC and MN either meet at
one point or are parallel.
Figure 56 (5.68)
b) Prove further that if point Olies on line BD, then the intersection point of lines KL,
AC and MN lies on line P Q.
5.69. On lines BC,CA and AB points A1,B1and C1are taken. Let P1be an arbitrary
point of line BC, let P2be the intersection point of lines P1B1and AB, let P3be the