Véc tơ ngẫu nhiên
1. Phân phối đồng thời của các biến ngẫu nhiên
Giả sử X1,X2,…,Xn là n biến ngẫu nhiên xác định trên cùng không gian xác suất
( , , P), nhận giá trị trong không gian đo (R, B(R).
Định nghĩa 1.1. Ta gọi X = (X1, X2,…, Xn) là vectơ ngẫu nhiên n chiều với giá trị
trong Rn.
Định nghĩa 1.2. Với mỗi tập Bôren B Bn, trong đó Bn là -đại số Bôren các tập
con của Rn, P[ : X B] được gọi là phân phối xác suất của vectơ ngẫu nhiên X
= (X1, X2,…, Xn) hay phân phối đồng thời của n biến ngẫu nhiên X1, X2,…, Xn.
Định nghĩa 1.3. Với (x1, x2,…, xn) Rn, hàm
F(x1, x2,…, xn) =
được gọi là hàm phân phối đồng thời của n biến ngẫu nhiên X1, X2,…, Xn.
Tính chất 1.4.
F(x1, x2,…, xn) là hàm đơn điệu không giảm theo các biến.
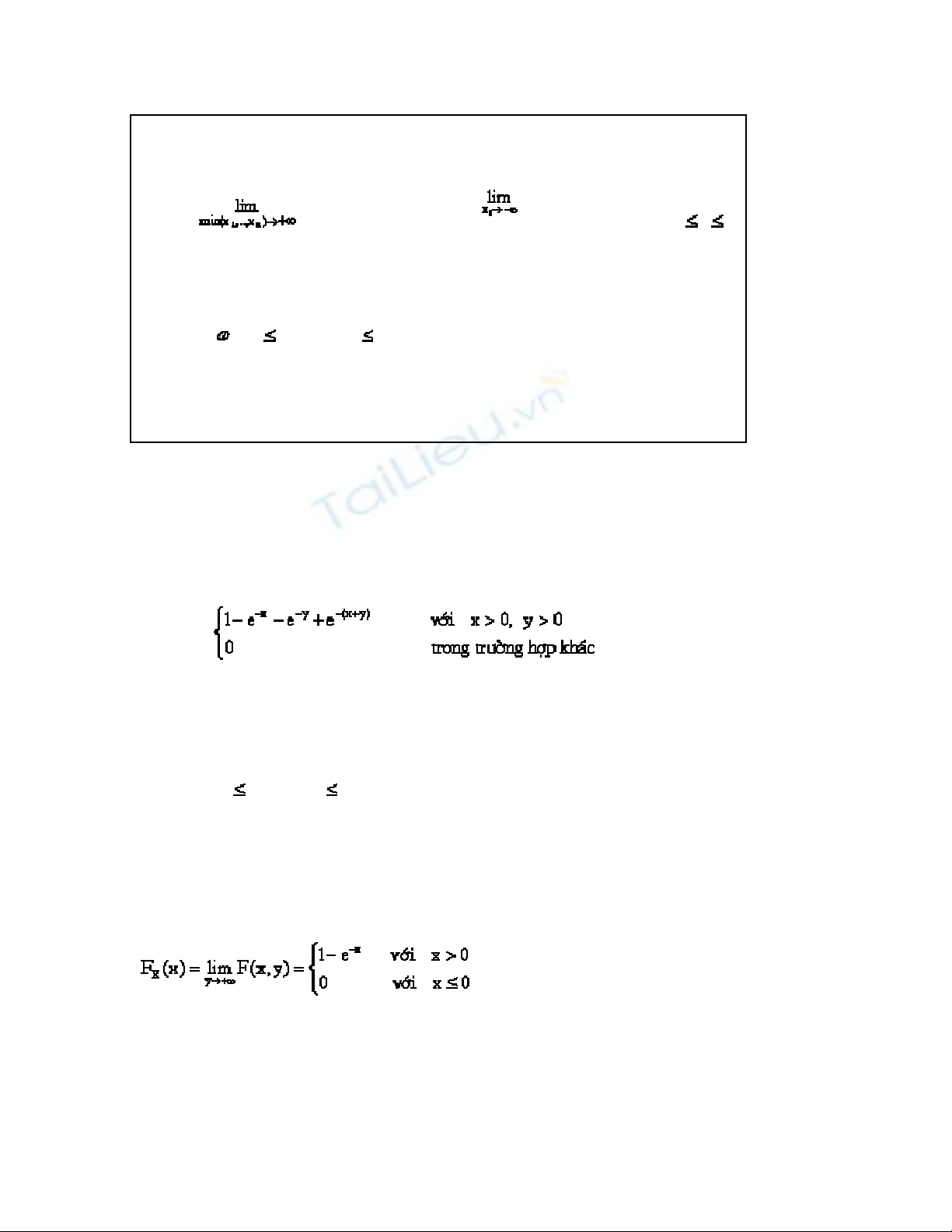
F(x1, x2,…, xn) là hàm liên tục bên phải theo các biến.
F(x1, x2,…, xn) = 1 và F(x1,x2,…,xn) = 0, 1 i
n.
P[ : a1 X < b1; a2 Y < b2] = F(b1,b2) – F(a1;b2) - F(b1;a2) +
F(a1;a2)
Ví dụ 1.5. Giả sử vectơ ngẫu nhiên (X, Y) có hàm phân phối đồng thời là
F(x,y) =
a- Xác định hàm phân phối của X ; của Y.
b- Tính P1 X < 2; 1 Y < 2]
Giải. a- Hàm phân phối của X là
Hàm phân phối của Y là
b- P[ 1 X < 2; 1 Y < 2] = F(2; 2) – F(1; 2) – F(2; 1) + F(1;1)
= 1 -
=
2. Véc tơ ngẫu nhiên rời rạc
Ta xét trường hợp 2 chiều. Cho X và Y là hai biến ngẫu nhiên rời rạc. Giả sử X
nhận các giá trị x1, x2,...., xn,...và Y nhận các giá trị y1, y2,... ym,...
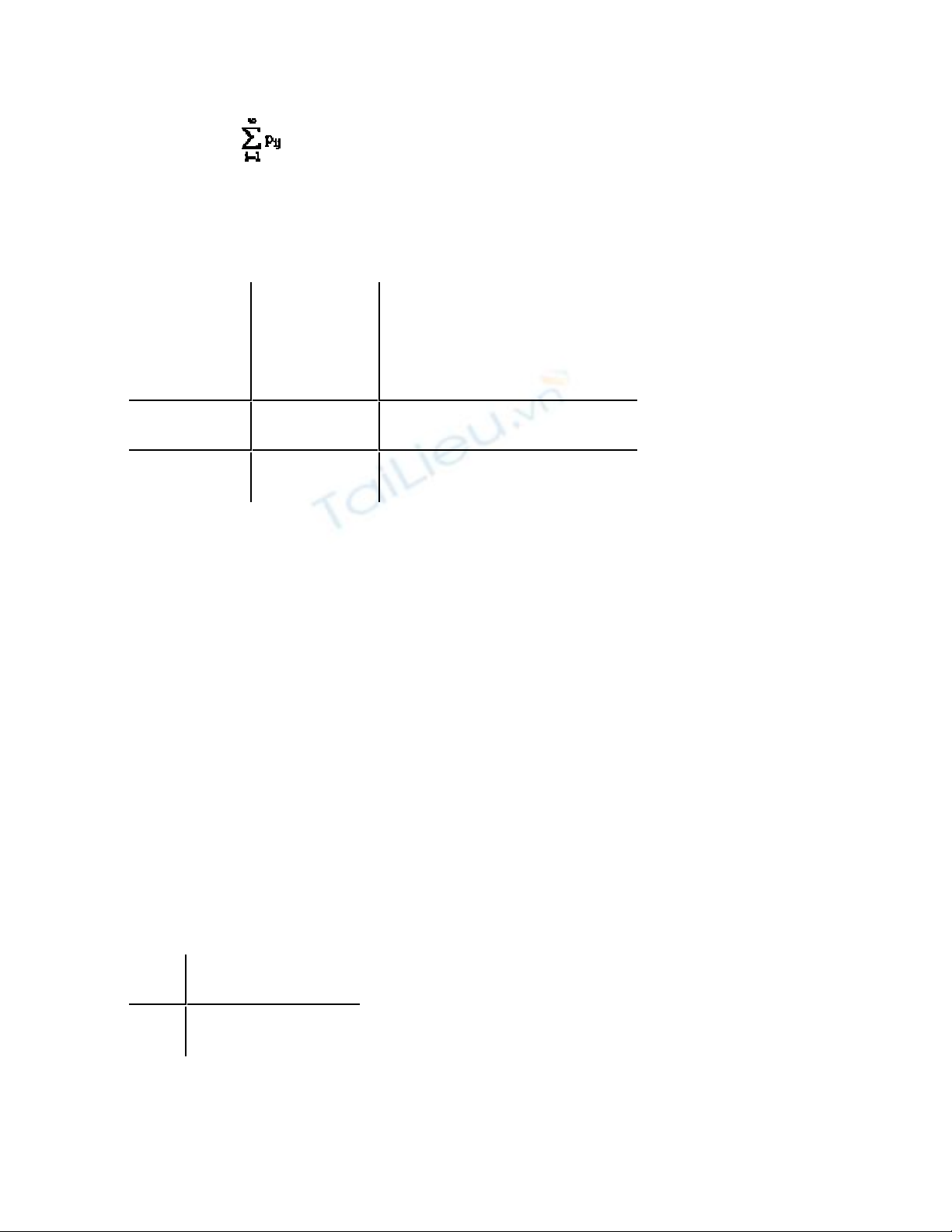
Định nghĩa 2.1. Dãy các xác suất
P([ : X = xi] [ : Y = yj]) =P(X = xi, Y = yi) = pij , i = 1, 2... và j = 1, 2,...
được gọi là phân phối đồng thời của hai biến ngẫu nhiên X, Y.
Ta có thể viết dưới dạng bảng như sau
-- page
break --
y1 Y2 ..... ym ....
Y
X
x1 p11 P12 ...... p1m ....
x2 p21 P22 ..... p2m ....
xn pn1 pn2 .... pnm ...
.... .... .... .... ....
Hàm phân phối đồng thời của X và Y là
F(x,y) = (x;y) R2.
Từ phân phối đồng thời của X và Y ta nhận được
Ø Phân phối xác suất của X là
P[X = xi] = , i = 1, 2,...
Ø Phân phối xác suất của Y là
P[Y = yi] = , j = 1, 2,...
Ví dụ 2.2. Cho vectơ ngẫu nhiên (X, Y) có phân phối đồng thời xác định như sau
X
Y
1 2 3
1 0,1 0,3 0,2
2 0,06 0,18 0,16
Tìm phân phối xác suất của X ; của Y và của Z = X + Y.
Giải. Ta có
P [X = 1] = 0,1 + 0,06 = 0,16;
P [X = 2] = 0,3 + 0,18 = 0,48;
P [X = 3] = 0,2 + 0,16 = 0,36;
Vậy phân phối xác suất của X là
X 1 2 3
P 0,16 0,48 0,36
Tương tự,