Nguyn Phú Khánh – à Lt
86
Bài 3 :TIM CN HÀM S
3.1TÓM TT LÝ THUYT
1. ng tim cn ng và ng tim cn ngang:
•
ng thng
=
c gi là ng tim cn ngang ( gi tt là tim cn
ngang) ca  th hàm s
(
)
=nu
(
)

→+∞
=
hoc
(
)

→−∞
=
.
•
ng thng
=
c gi là ng tim cn ng ( gi tt là tim cn
ng) ca  th hàm s
(
)
=
nu
(
)

−
→
= +∞
hoc
(
)

+
→
= +∞
hoc
(
)

−
→
= −∞
hoc
(
)

+
→
= −∞
.
2. ng tim cn xiên:
ng thng
(
)

= + ≠
c gi là ng tim cn xiên ( gi tt là
tim cn xiên) ca  th hàm s
(
)
=
nu
(
)
(
)
(
)


→+∞
= − + =
hoc
(
)
(
)
(
)


→−∞
= − + =
Trong ó
(
)
( )
 

→+∞ →+∞
= = −
hoc
(
)
( )
 

→−∞ →−∞
= = −
.
Chú ý : Nu
=
thì tim cn xiên tr thành tim cn ng.
3.2 DNG TOÁN THNG GP
Ví d 1 : Tìm tim cn ca  th hàm s :

−
=
+

− +
=
−

+
=

= + −
Gii :

−
=
+
Hàm s ã cho xác nh và liên tc trên
{
}
=
.
Nguyn Phú Khánh – à Lt
87
Ta có:
  
→−∞ →−∞ →−∞
−
−
= = =
++
và
  
→+∞ →+∞ →+∞
−
−
= = =
++
=
là tim cn ngang ca  th khi
→ −∞
và
→ +∞
.
( ) ( )
 
− −
→ − → −
−
= = −∞
+ và
( ) ( )
 
+ +
→ − → −
−
= = +∞
+
= −
là tim cn ng ca  th khi
( )
−
→ −
và
( )
→ −
;
( )
 
→−∞ →−∞
−
= =
+ hàm s
không
có tim cn xiên khi
→ −∞
.
( )
  
→+∞ →+∞ →+∞
−
−
= = =
+
+ hàm s
không có tim cn
xiên khi
→ +∞
.

− +
=
−
Hàm s ã cho xác nh và liên tc trên
{
}
=
Ta có:
= +
−
 
+ +
→ →
= + = +∞
−
và
 
− −
→ →
= + = −∞ =
−
là tim cn ng ca  th hàm s
khi
+
→
và
−
→
;
 
→+∞ →+∞
= + = +∞
−
và
 
→−∞ →−∞
= + = −∞
−
hàm s không có tim cn ngang
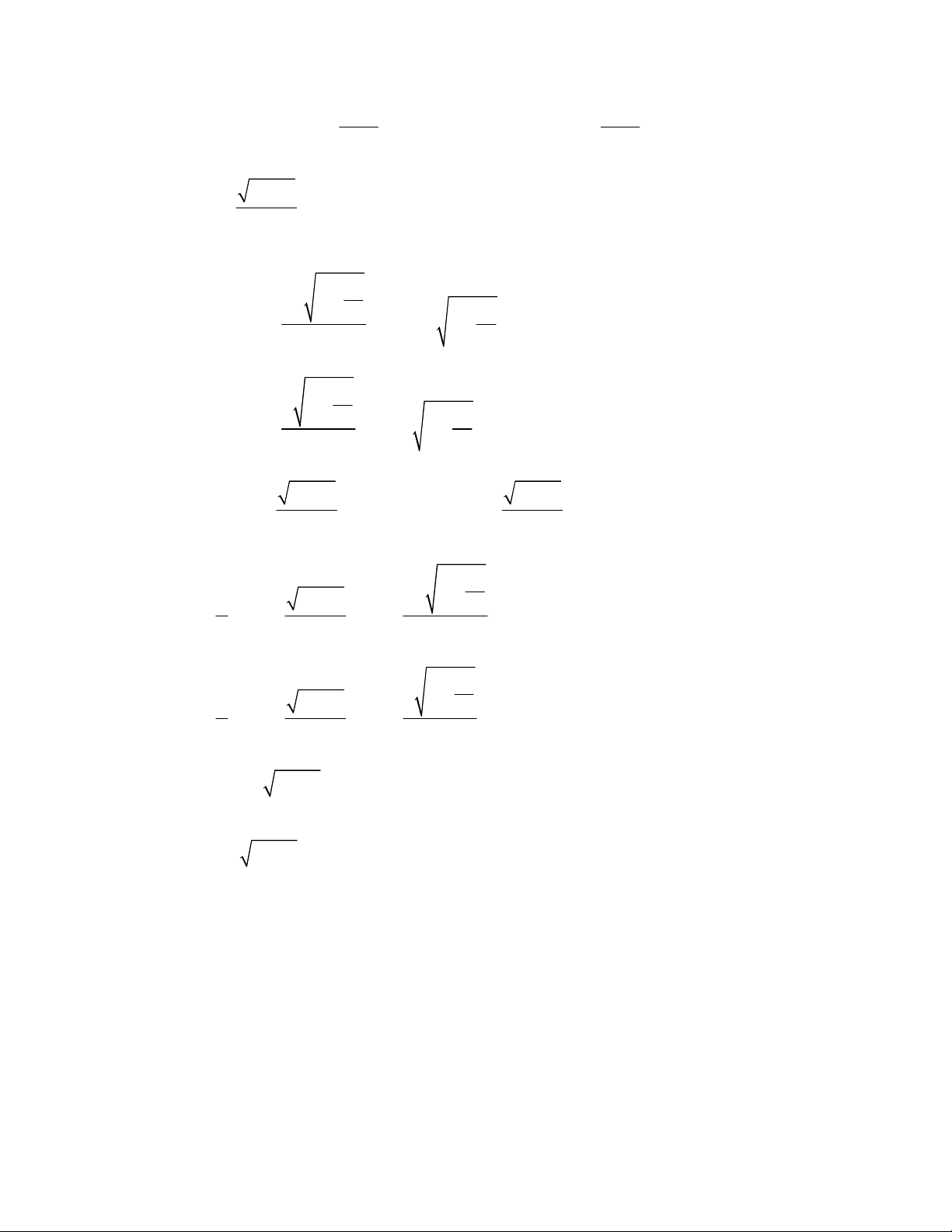
Nguyn Phú Khánh – à Lt
88
 
→+∞ →+∞
− = =
−
và
 
→−∞ →−∞
− = =
−
=
là tim cn xiên ca  th hàm s khi
→ +∞
và
→ −∞
.

+
=
Hàm s ã cho xác nh và liên tc trên
{
}
=
.
  
→−∞ →−∞ →−∞
− +
= = − + = − = −
là tim cn ngang
ca  th hàm s khi
→ −∞
.
  
→+∞ →+∞ →+∞
+
= = + = =
là tim cn ngang ca 
th hàm s khi
→ +∞
.
   
− − + +
→ → → →
+ +
= = −∞ = = +∞
=
là tim cn
ng ca  th hàm s khi
−
→
và
+
→
  
→−∞ →−∞ →−∞
− +
+
= = =
hàm s
không có tim cn
xiên khi
→ −∞
  
→+∞ →+∞ →+∞
+
+
= = =
hàm s
không có tim cn xiên
khi
→ +∞

= + −
( )
− ≤ ≤
= + − ⇔ ≥
+ − =
Do ó  th hàm s là na ng tròn tâm
(
)
, bán kính
=
.
Vy  th hàm s không có tiêm cn.
Chú ý :
Nguyn Phú Khánh – à Lt
89
Cho hàm phân thc
=
.
a) S tim cn ng ca  th hàm s là s nghim ca h
=
≠
.
b)  th hàm s có tim cn ngang
⇔
 
≤
, trong ó

là
bc ca a thc.
c)  th hàm s có tim cn xiên
 
⇔ = +
.Khi ó  tìm
tim cn xiên ta chia
cho
, ta c:
= + +
, trong ó
 
<
 
→+∞ →−∞
= = = +
là TCX ca  th hàm s.
* Nu  th hàm s có tim cn ngang thì không có tim cn xiên và ngc li.
Bài tp t luyn:
Tìm tim cn ca  th hàm s :
1.
−
=
+
2.
+ −
=
−
3.
= + + +
2.
+ +
=
+
Ví d 2: Tìm tim cn ca các  th hàm s sau:

= − +

= + −
Gii :

= − +
Hàm s ã cho xác nh và liên tc trên
.
Ta có:
  
→+∞ →+∞ →+∞
− +
= = = − + =
 

→+∞ →+∞
= − = − + −
 
→+∞ →+∞
− +
− +
= = = −
− + + − + +
= −
là tim cn xiên ca  th hàm s khi
→ +∞
.
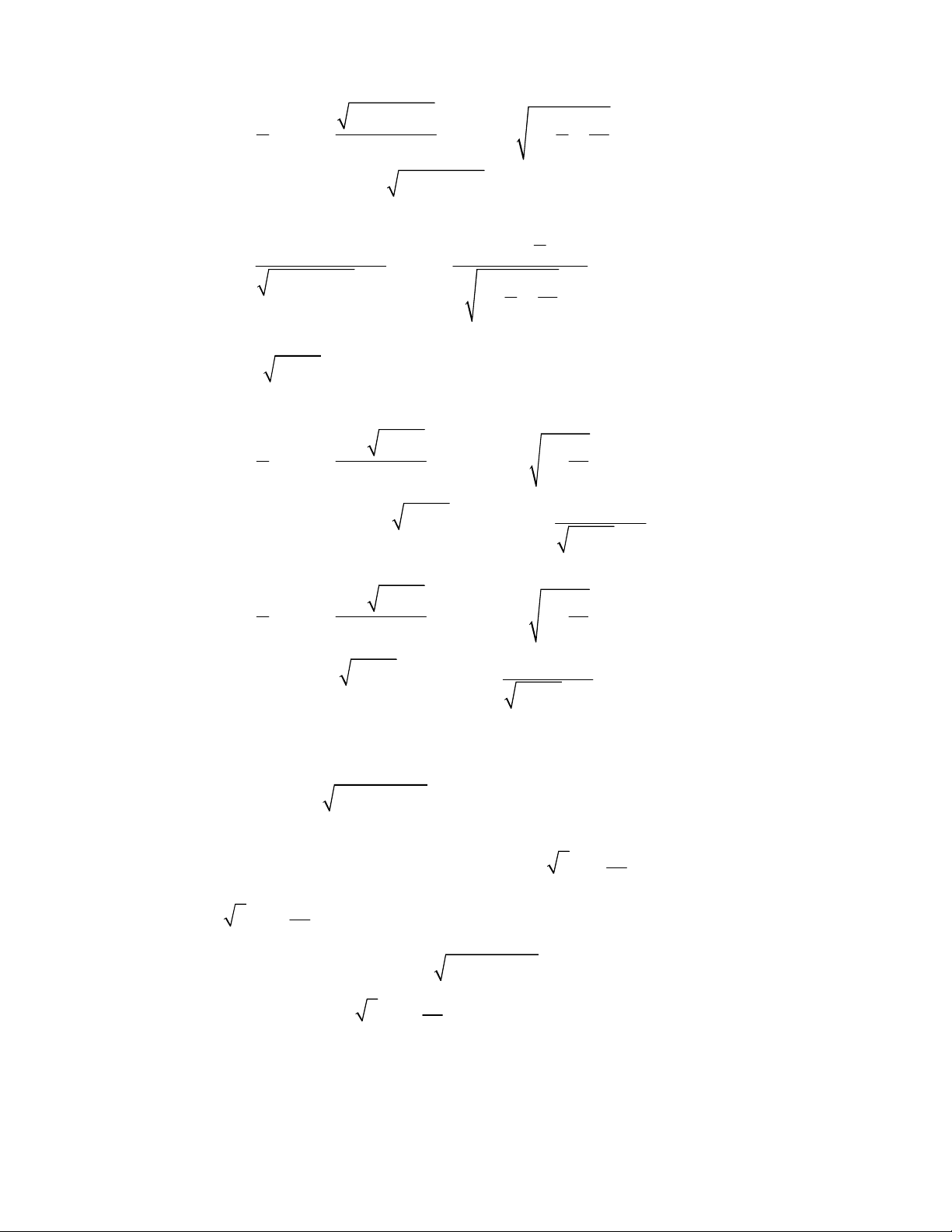
Nguyn Phú Khánh – à Lt
90
  
→−∞ →−∞ →−∞
− +
= = = − − + = −
 

→−∞ →−∞
= − = − + +
 
→−∞ →−∞
− +
− +
= = =
− + − − − + −
= − +
là tim cn xiên ca  th hàm s khi
→ −∞
.

= + −
Hàm s ã cho xác nh và liên tc trên
(
)
= −∞ − ∪ +∞
.
  
→+∞ →+∞ →+∞
+ −
= = = + − =
( )
  

→+∞ →+∞ →+∞
−
= − = − − = =
− +
=
là tim cn xiên ca  th hàm s khi
→ +∞
.
  
→−∞ →+∞ →+∞
+ −
= = = − − =
  
→−∞ →−∞ →−∞
−
= = − + = =
− −
=
là tim cn ngang ca  th hàm s khi
→ −∞
.
Nhn xét:
1) Xét hàm s

 
= + + ≠
.
* Nu
<
 th hàm s không có tim cn.
* Nu
>
 th hàm s có tim cn xiên
= +
khi
→ +∞
và
= − +
khi
→ −∞
.
2)  th hàm s
  
= + + + +
>
có tim cn là ng
thng :

= + + +
.