Bài giảng Cơ học Lý thuyết - Tuần 5 4/3/2011
Giảng viên Nguyễn Duy Khương 1
CHƯƠNG 8 Chuyểnđộng phứchợpcủađiểm
1. Định lý hợpvậntốcvàgiatốc
2. Các bài toán ví dụ
NỘI DUNG
CHƯƠNG 8 Chuyểnđộng phứchợpcủađiểm
1. Định lý hợp vận tốc và gia tốc
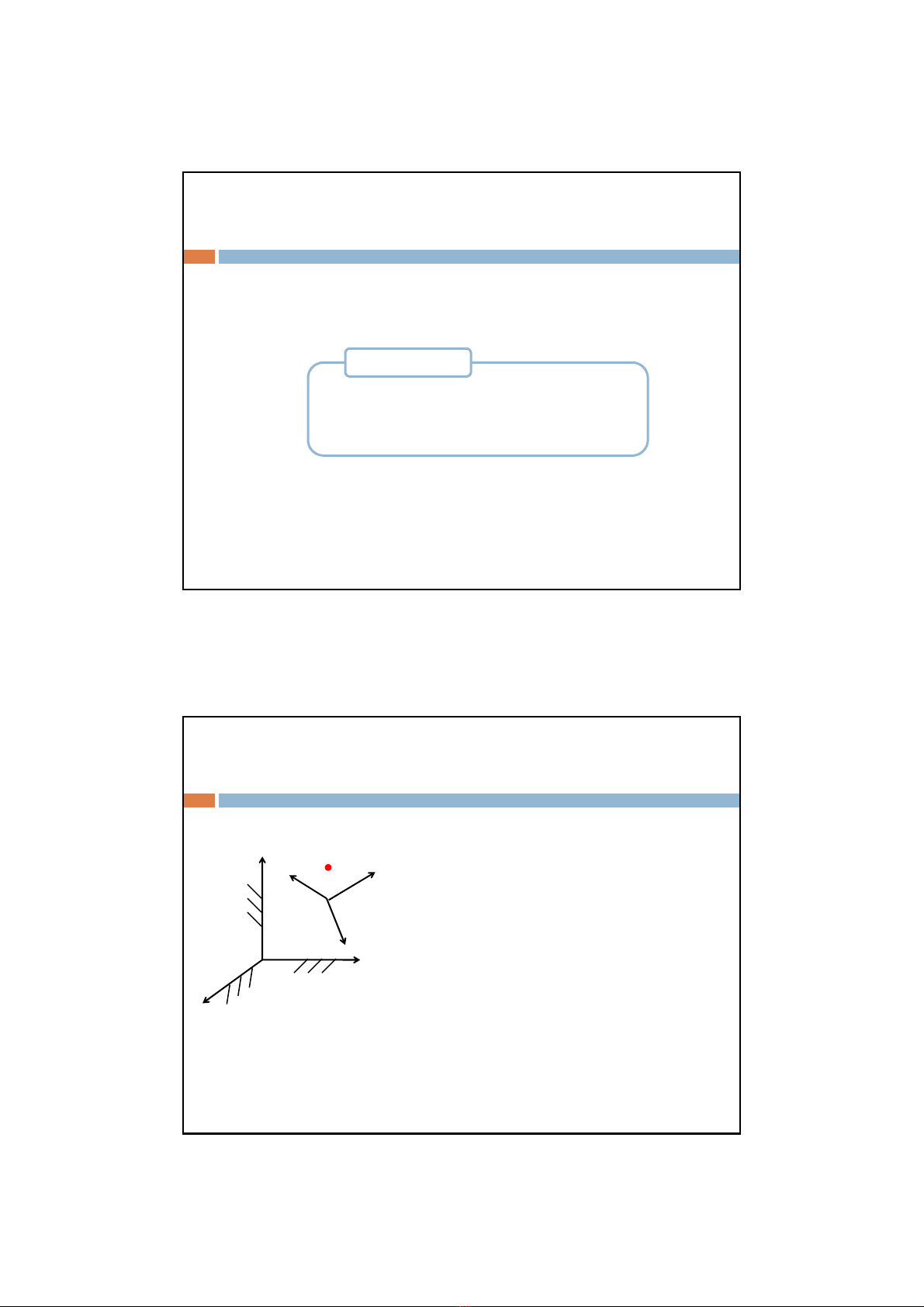
Định nghĩa chuyển động
My1
x1
z1
O1
x
y
z
O
•Chuyển động tuyệt đối:
Là chuyển động của điểm M so với hệ
trục cố định Oxyz
•Chuyển động tương đối:
Là chuyển động của điểm M so với hệ
trục động O1x1y1z1
•Chuyển động kéo theo:
Là chuyển động của điểm hệ trục cố
định Oxyz so với hệ trục động O1x1y1z1
Vận tốc và gia tốc tuyệt đối là: ,
aa
VW
Vận tốc và gia tốc tương đối là: ,
rr
VW
Vận tốc và gia tốc kéo theo là: ,
ee
VW
Bài giảng Cơ học Lý thuyết - Tuần 5 4/3/2011
Giảng viên Nguyễn Duy Khương 2
CHƯƠNG 8 Chuyểnđộng phứchợpcủađiểm
1. Định lý hợp vận tốc và gia tốc
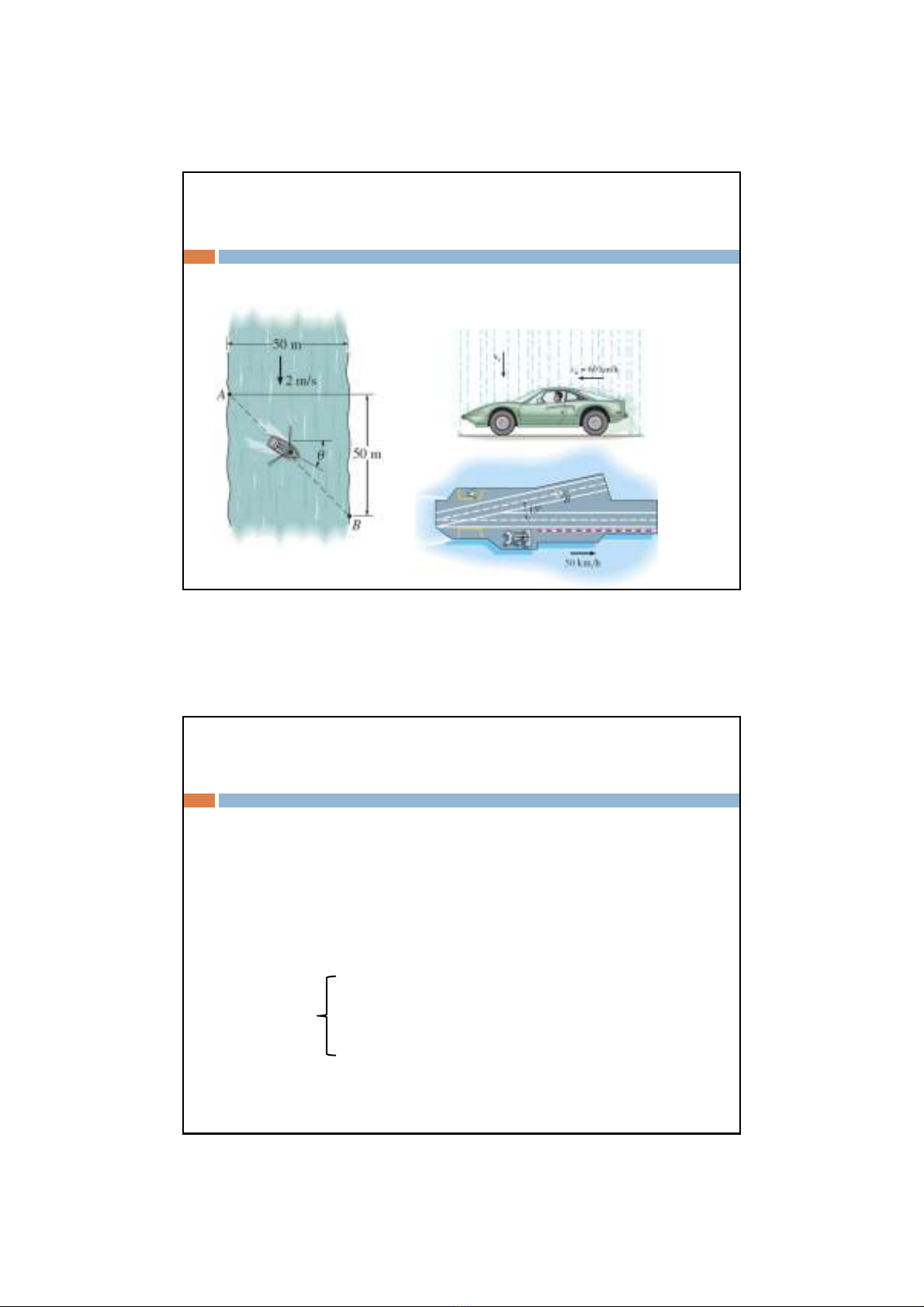
Xác định chuyển động: Chuyển động tuyệt đối ?
Chuyển động tương đối?
Chuyển động kéo theo?
CHƯƠNG 8 Chuyểnđộng phứchợpcủađiểm
1. Định lý hợp vận tốc và gia tốc
Định lý hợp vận tốc:
are
VVV
Định lý hợp gia tốc:
areC
WWWW
Với2( )
Cer
WV
là gia tốc Coriolis
Nếu hệ động chuyển động tịnh tiến thì 00
eC
W
Phương: vuông góc vớivà
Chiều: lấy quay theo chiều90
0
r
V
e
r
V
e
Độ lớn: 2
Cer
WV
C
W
Bài giảng Cơ học Lý thuyết - Tuần 5 4/3/2011
Giảng viên Nguyễn Duy Khương 3
CHƯƠNG 8 Chuyểnđộng phứchợpcủađiểm
2. Các bài toán ví dụ
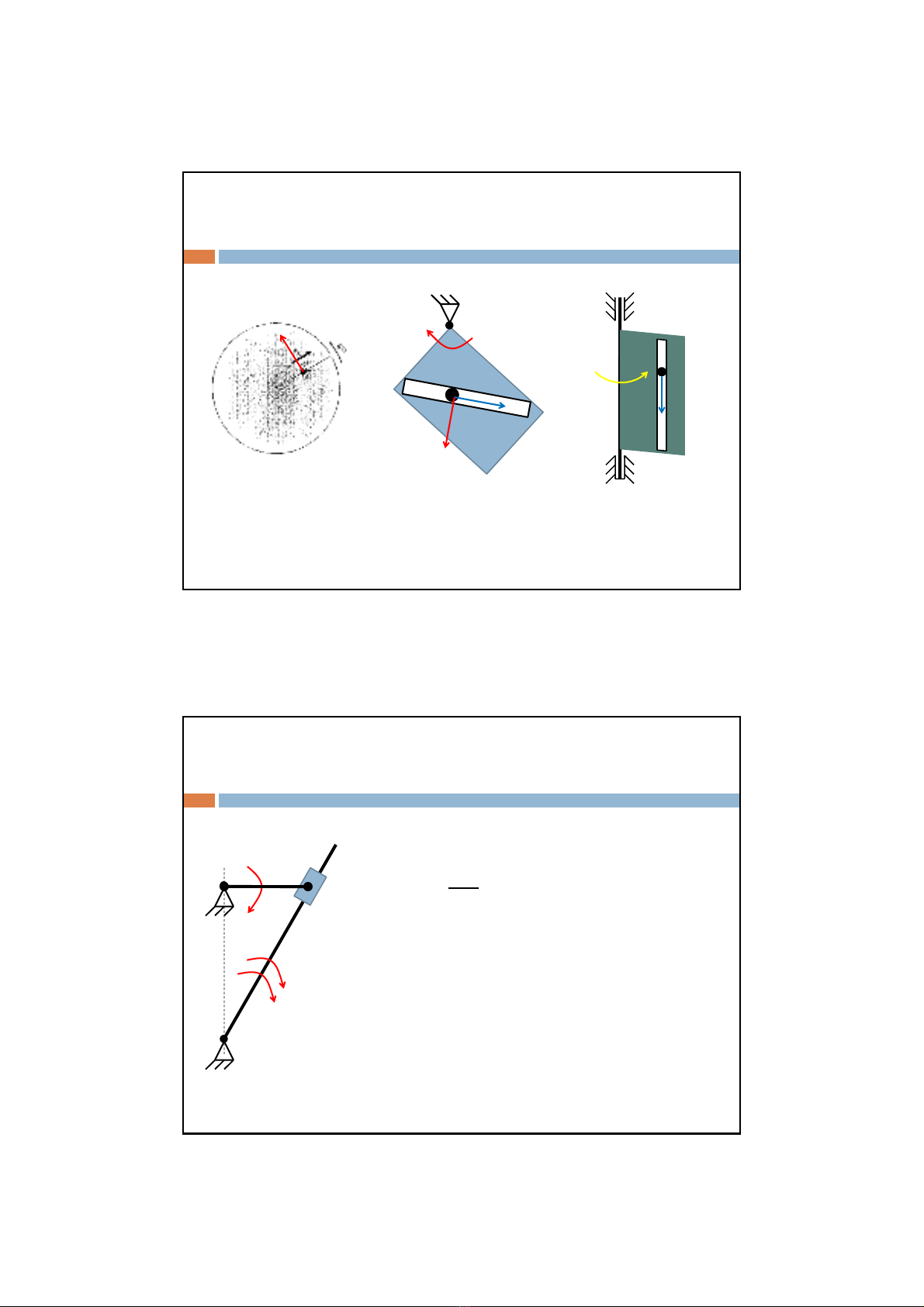
Ví dụ: Xác định gia tốc Coriolis
00
2
C
Wv
V
2
C
WV
V
0
C
W
CHƯƠNG 8 Chuyểnđộng phứchợpcủađiểm
2. Các bài toán ví dụ
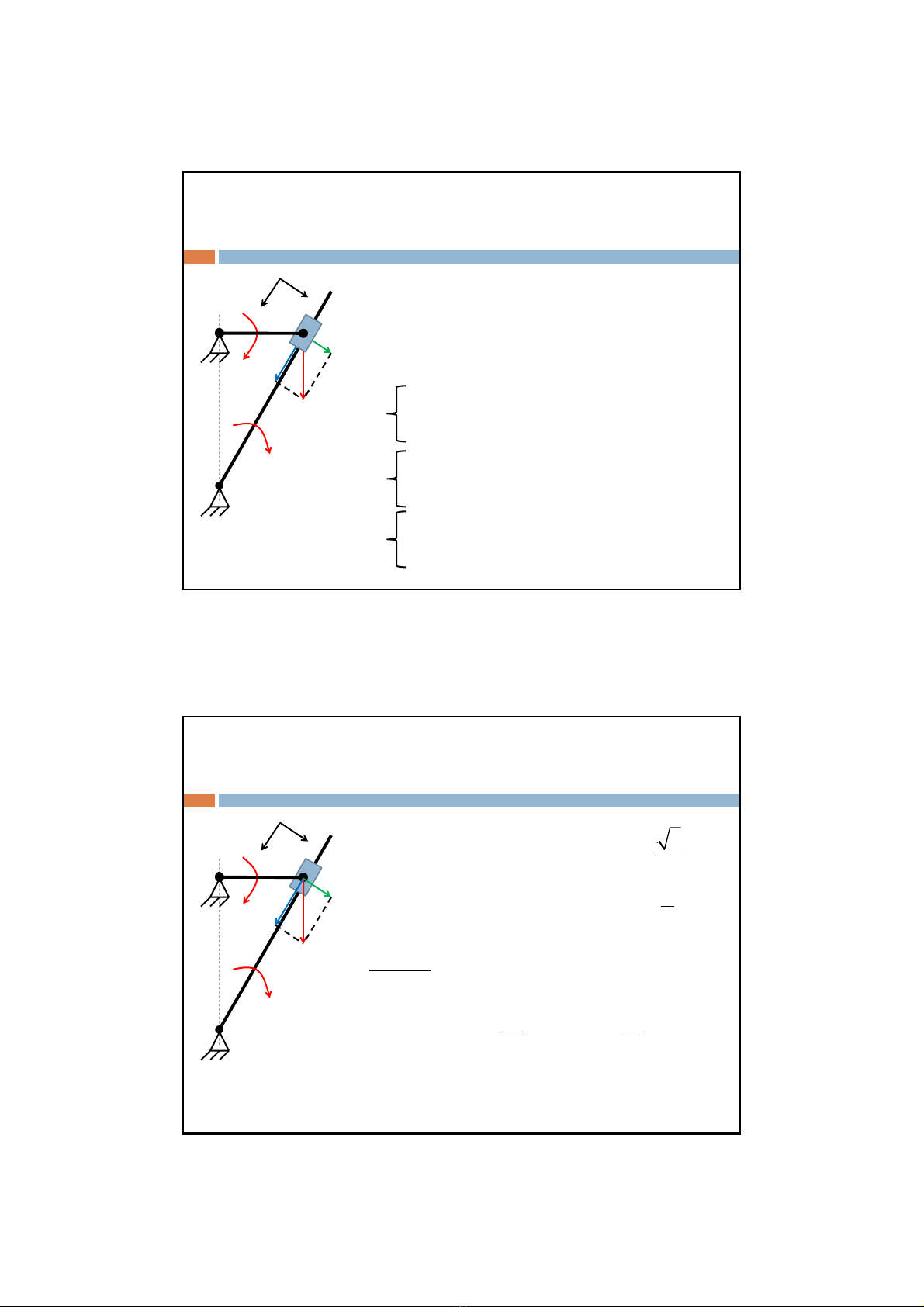
Ví dụ: Cho cơ cấu sau
0
0
30
O
1
O
A
B
1
1
Biết , ,OA=R
0
00
Tính vận tốc góc và gia tốc góc thanh O1B.
Giải
*Chọn thanh O1B làm hệ động.
*Phân tích chuyển động
Chuyển động của con lăn A quay quanh O
Chuyển động của con lăn A trượt trên O1B
+Chuyển động tuyệt đối
+Chuyển động tương đối
+Chuyển động kéo theo
Chuyển động của con lăn A quay quanh O1
Bài giảng Cơ học Lý thuyết - Tuần 5 4/3/2011
Giảng viên Nguyễn Duy Khương 4
CHƯƠNG 8 Chuyểnđộng phứchợpcủađiểm
2. Các bài toán ví dụ
*Giải bài toán vậntốc
a
V
r
V
e
V
are
VVV
(*)
Gặp phương trình vector thì chiếu
lên HAI phương vuông góc
x
y
Phân tích vector
a
V
Phương: vuông góc vớiOA
Độ lớn: 0a
VR
r
V
Phương: cùng phương vớiO
1B
Độ lớn: r
V
e
V
Phương: vuông góc vớiO
1B
Độ lớn: 1
2
e
VR
0
0
30
O
1
O
A
B
1
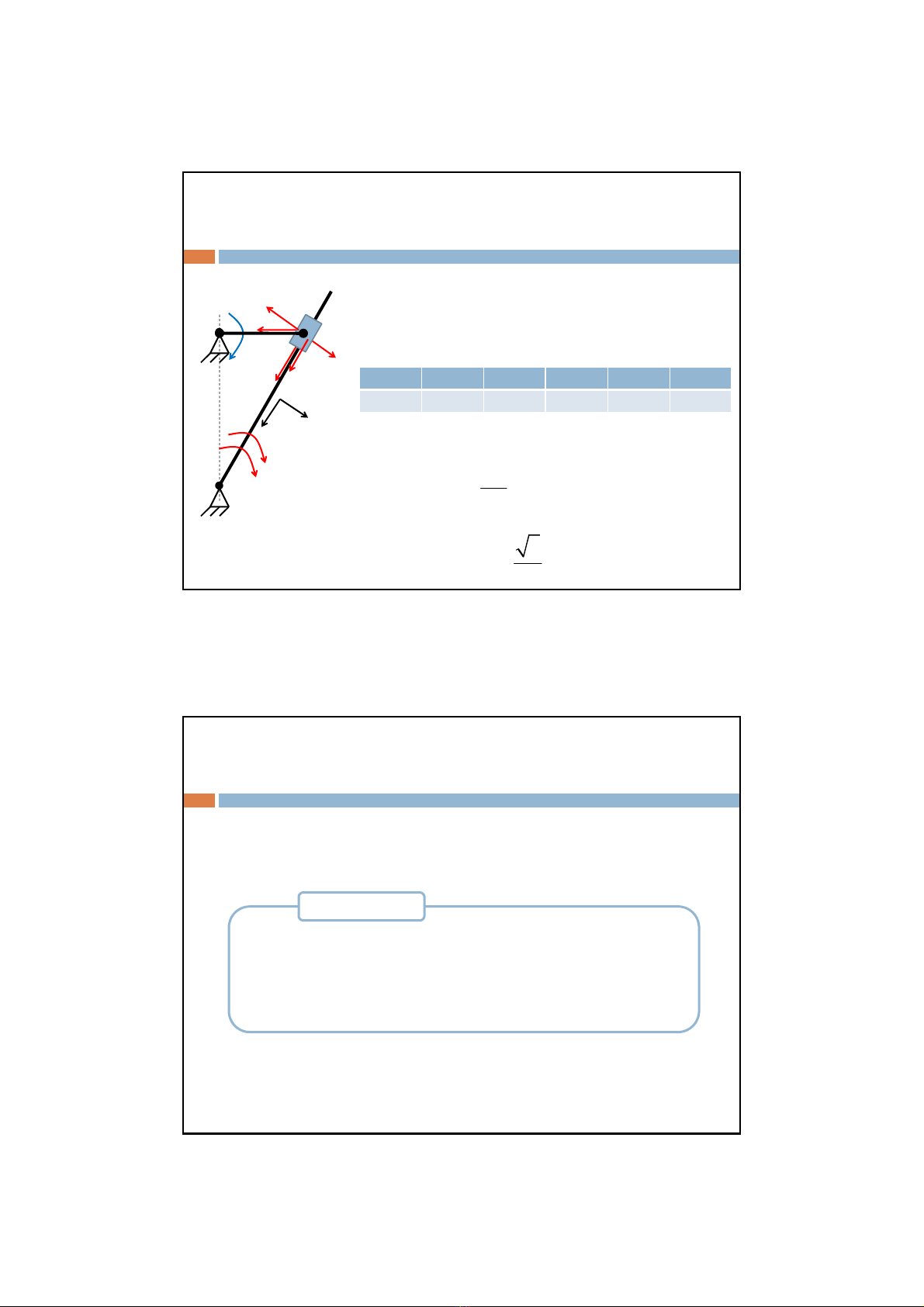
CHƯƠNG 8 Chuyểnđộng phứchợpcủađiểm
2. Các bài toán ví dụ
a
V
0
0
30
O
1
O
A
B
r
V
e
V
Chiếu (*) lên trục x, y
x
yOx: 0
cos 30 0
ra
VV
0
3
2
r
V
R
Oy: 0
sin 30 0
ae
VV
10
1
4
Cách 2:
Vì hai vector vuông góc
0
cos30
a
r
V
V
0
sin30
a
e
V
V
1
Bài giảng Cơ học Lý thuyết - Tuần 5 4/3/2011
Giảng viên Nguyễn Duy Khương 5
CHƯƠNG 8 Chuyểnđộng phứchợpcủađiểm
2. Các bài toán ví dụ
*Giải bài toán gia tốc
areC
WWWW
n
a
W
r
W
e
W
x
y
0
0
30
O
1
O
A
B
1
1
(*)
nn
aa reeC
WW WWWW
|_ OA //OA //O1B|_ O
1B//O1B|_ O
1B
00R
2
0
R
r
W2
1
2
R
1
2
R
1
2r
V
Chiếu (*) lên trục x, y
Ox:
Oy:
20 2
01
0sin30 020
r
W
RR
n
e
W
C
W
2
0
3
8
r
R
W
2
1
1
0
0
0 cos30 0 2 0 2 r
R
RV
2
0
1
3
8
CHƯƠNG 9 Chuyểnđộng song phẳng củavậtrắn
1. Khảosátvật chuyểnđộng song phẳng
2. Những chuyểnđộng song phẳng đặcbiệt
NỘI DUNG
3. Những bài toán ví dụ











![Đề thi học kì 1 Vật lý lớp 1 năm 2025-2026 (Đề số 2) [Có đáp án]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260210/hoahongcam0906/135x160/1981770793442.jpg)



![Đề thi học kỳ III Vật lý 1 năm 2024-2025 có đáp án [FULL]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260209/diegomaradona04/135x160/99561770719042.jpg)
![Bài tập Vật lý sóng: Tổng hợp bài tập 6 [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250805/oursky04/135x160/401768817575.jpg)









