Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 10
11/22/2011
Giảng viên Nguyễn Duy Khương 1
CHƯƠNG 5 Tính bềncácbàitoánthuộcdạng thanh
3. Tính bềncácbàitoánthuộcdạng thanh
II‐Thanh chịuuốnxiên
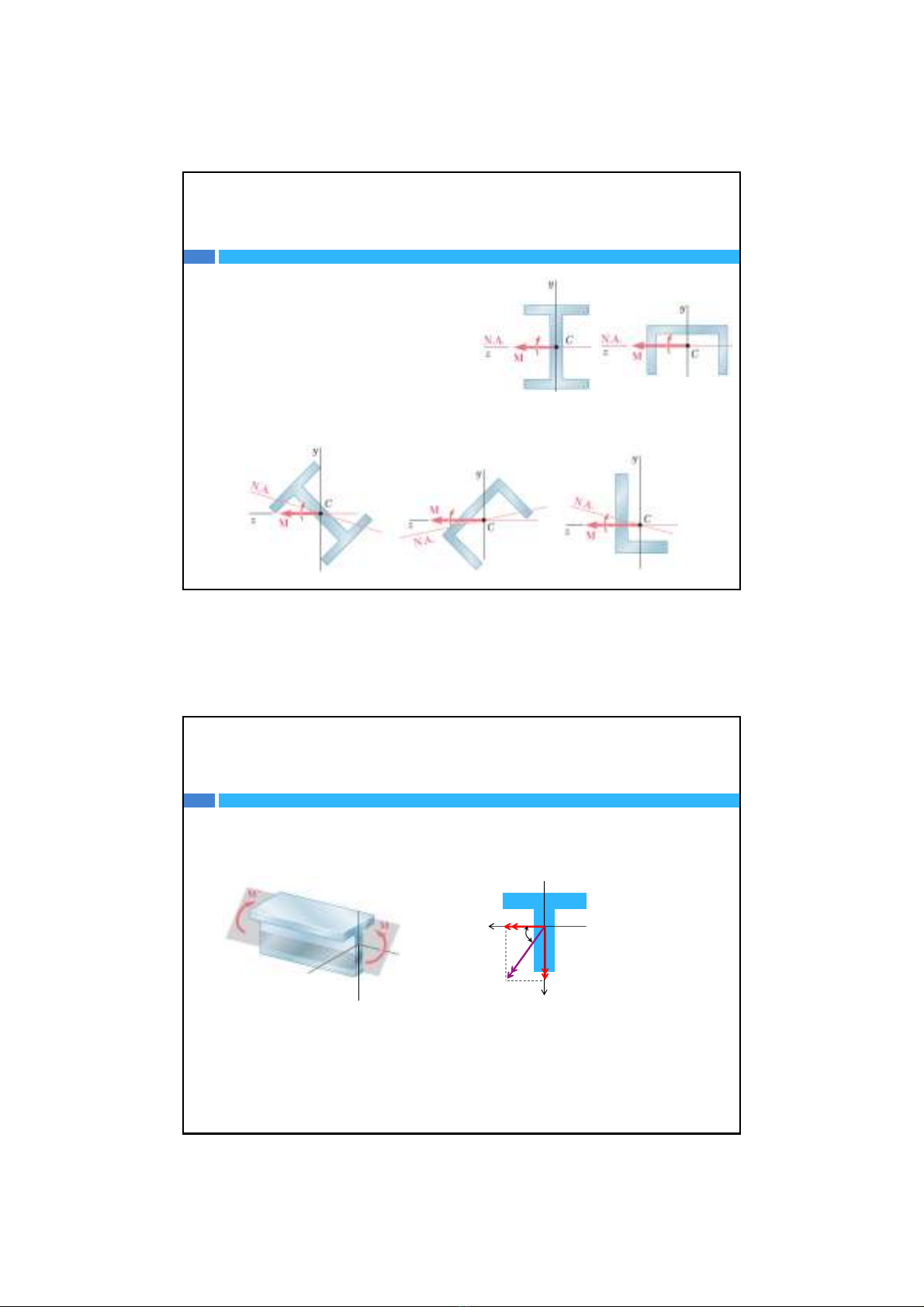
Trong trường hợpuốntrongmặt
phẳng trùng hoặc vuông góc vớitrục
đốixứng củamặtcắtngang.
Khi mặtphẳng uốn không trùng hoặckhôngvuônggócvớitrụcđốixứng
củamặtcắtngangtathanhnàyởtrạng thái uốnxiên.
CHƯƠNG 5 Tính bềncácbàitoánthuộcdạng thanh
3. Tính bềncácbàitoánthuộcdạng thanh
z
x
y
Trên mặtcắt có hai thành phầnnộilựclàmô‐men Mx,mô‐men My.Mỗi
thành phầnmô‐men đềucùnggâyraứng suất pháp z.Dođótrạng thái
ứng suất trong thanh chỉcó thành phầnứng suất pháp z.
Để khảo sát thanh, ta tách mô‐men uốntrênmặtphẳng không đốixứng
này thành hai thành phầnlàtrùngvớitrụcđốixứng và vuông góc với
trụcđốixứng (Mxvà My).
x
y
x
M
y
M
M
Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 10
11/22/2011
Giảng viên Nguyễn Duy Khương 2
CHƯƠNG 5 Tính bềncácbàitoánthuộcdạng thanh
3. Tính bềncácbàitoánthuộcdạng thanh
Thành phầnứng suất pháp zgây ra bởimô‐men Mxlà
x
z
x
M
y
J
Tương tự, thành phầnứng suất pháp zgây ra bởimô‐men Mylà
y
z
y
M
J

Sửdụng nguyên lý cộng tác dụng ta được thành phần
ứng suất pháp do cảmô‐men uốnM
xlẫnM
ygây ra
y
x
z
xy
M
M
y
x
J
J

M
x
y
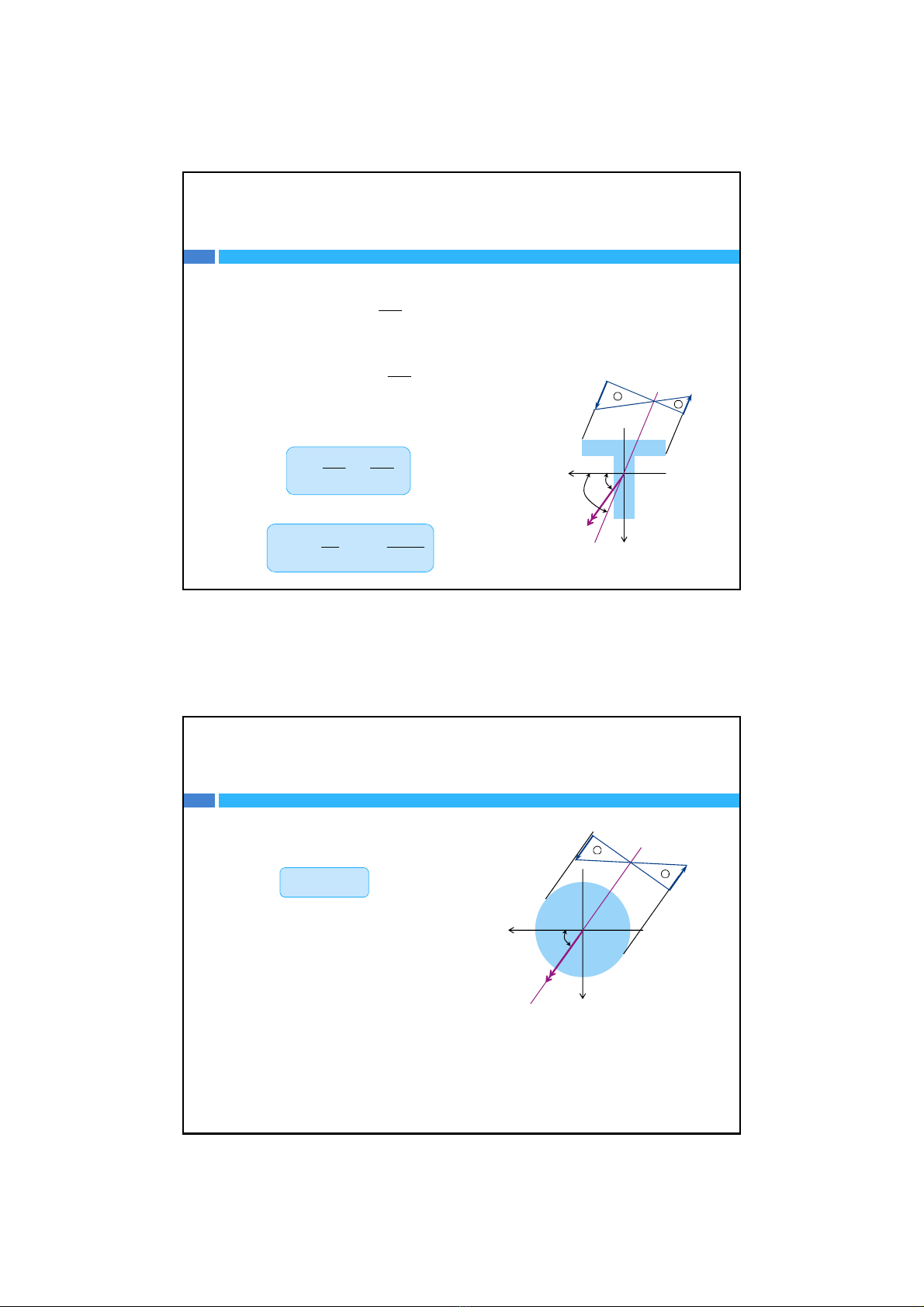
Phương củatrục trung hòa
tan tan
x
y
x
yyx
J
M
J
J
JM


trục trung hòa
,maxn
,maxk
+
-
CHƯƠNG 5 Tính bềncácbàitoánthuộcdạng thanh
3. Tính bềncácbàitoánthuộcdạng thanh
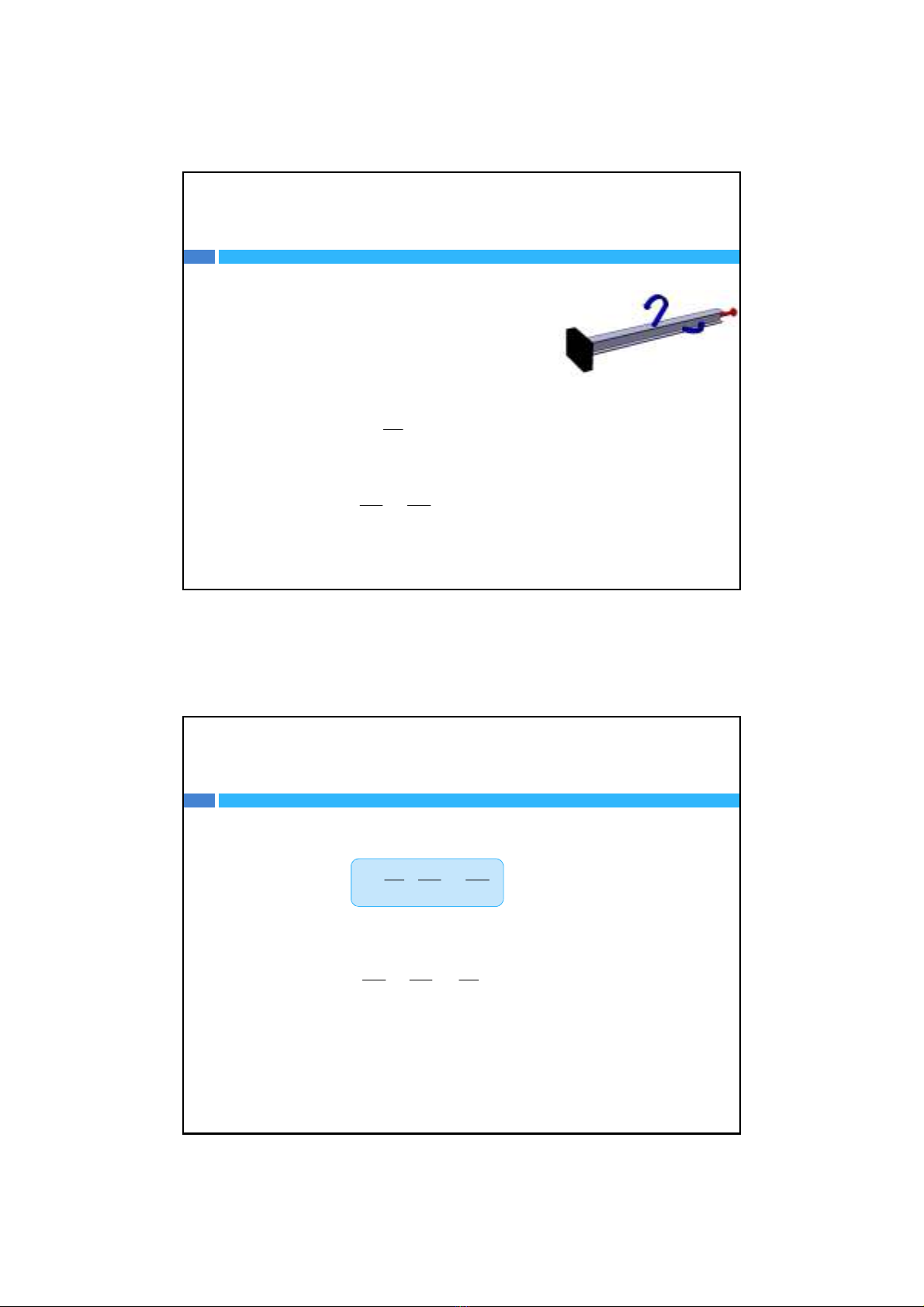
Đốivớimặtcắtlàhìnhtròntađược
tan tan
x
y
J
J
Vì thế
Nghĩalàtrục trung hòa trùng với
phương củavectormô‐men M. Trường
hợpnàygiống nhưmô‐men trung với
trụcđốixứng.
M
x
y
trục trung hòa
,maxn
,maxk
+
-
Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 10
11/22/2011
Giảng viên Nguyễn Duy Khương 3
CHƯƠNG 5 Tính bềncácbàitoánthuộcdạng thanh
3. Tính bềncácbàitoánthuộcdạng thanh
III‐Thanh chịuuốnkéonénđồng thời(kéonénlệch tâm)
Trên mặtcắt có ba thành phầnnộilựclàlựcdọc
trụcN
z,mô‐men Mx,mô‐men My.Dođótrạng thái
ứng suất trong thanh chỉcó thành phầnứng suất
pháp z.
Thành phầnứng suất pháp zgây ra bởilựcdọctrụcN
z
y
x
z
xy
M
M
y
x
J
J

Thành phầnứng suất pháp zgây ra bởimô‐men Mxvà Mylà
z
z
N
A
CHƯƠNG 5 Tính bềncácbàitoánthuộcdạng thanh
3. Tính bềncácbàitoánthuộcdạng thanh
Sửdụng nguyên lý cộng tác dụng ta được thành phầnứng suất pháp do
cảmô‐men uốnM
xlẫnM
ygây ra
y
x
z
z
xy
M
M
N
y
x
AJ J

Đường trung hòa tìm đượcbằng cách cho z=0, ta đượcphương trình
đường thẳng là phương trình đường trung hòa
yx
z
yx
MMN
xy
J
JA

Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 10
11/22/2011
Giảng viên Nguyễn Duy Khương 4
CHƯƠNG 5 Tính bềncácbàitoánthuộcdạng thanh
3. Tính bềncácbàitoánthuộcdạng thanh
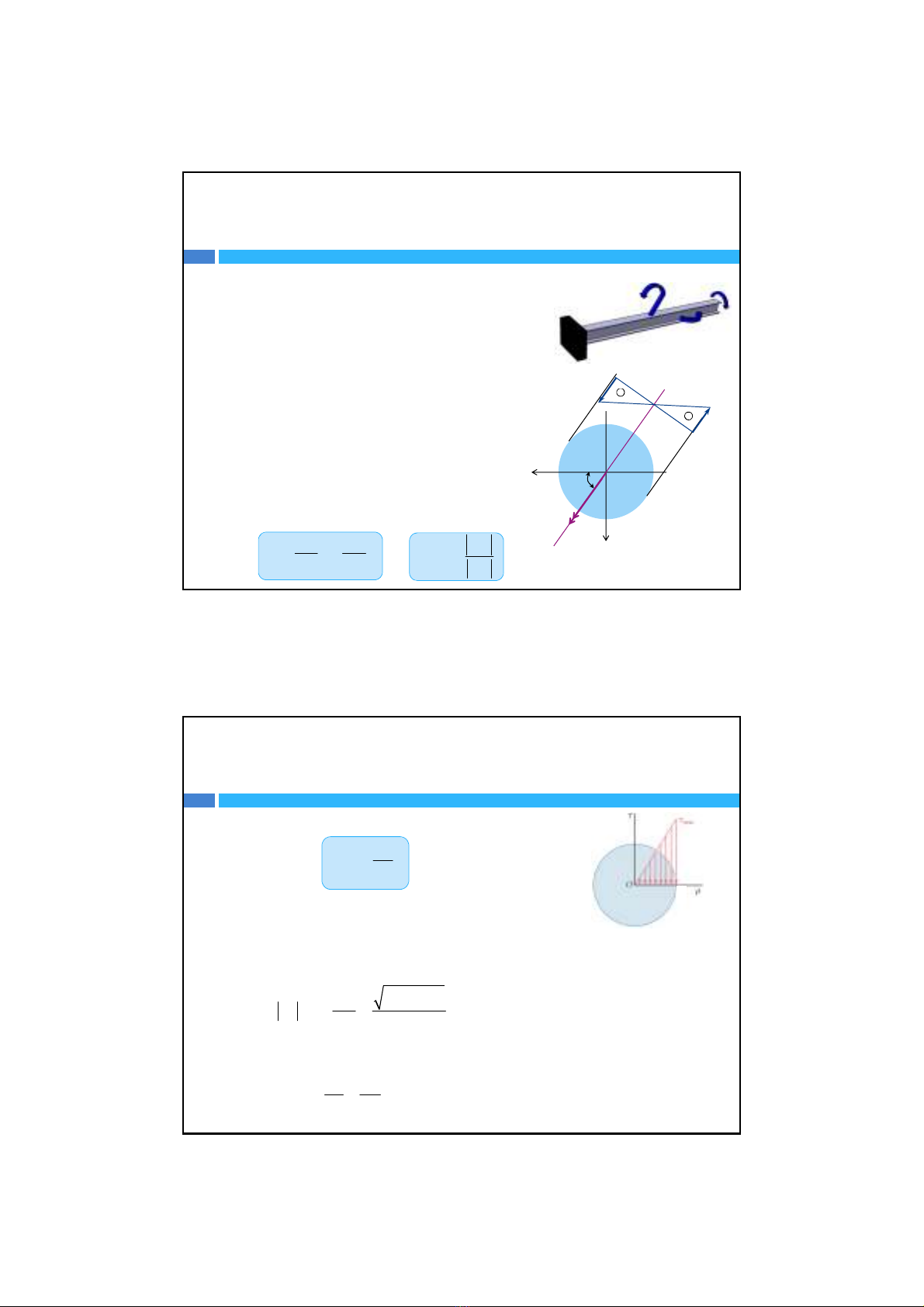
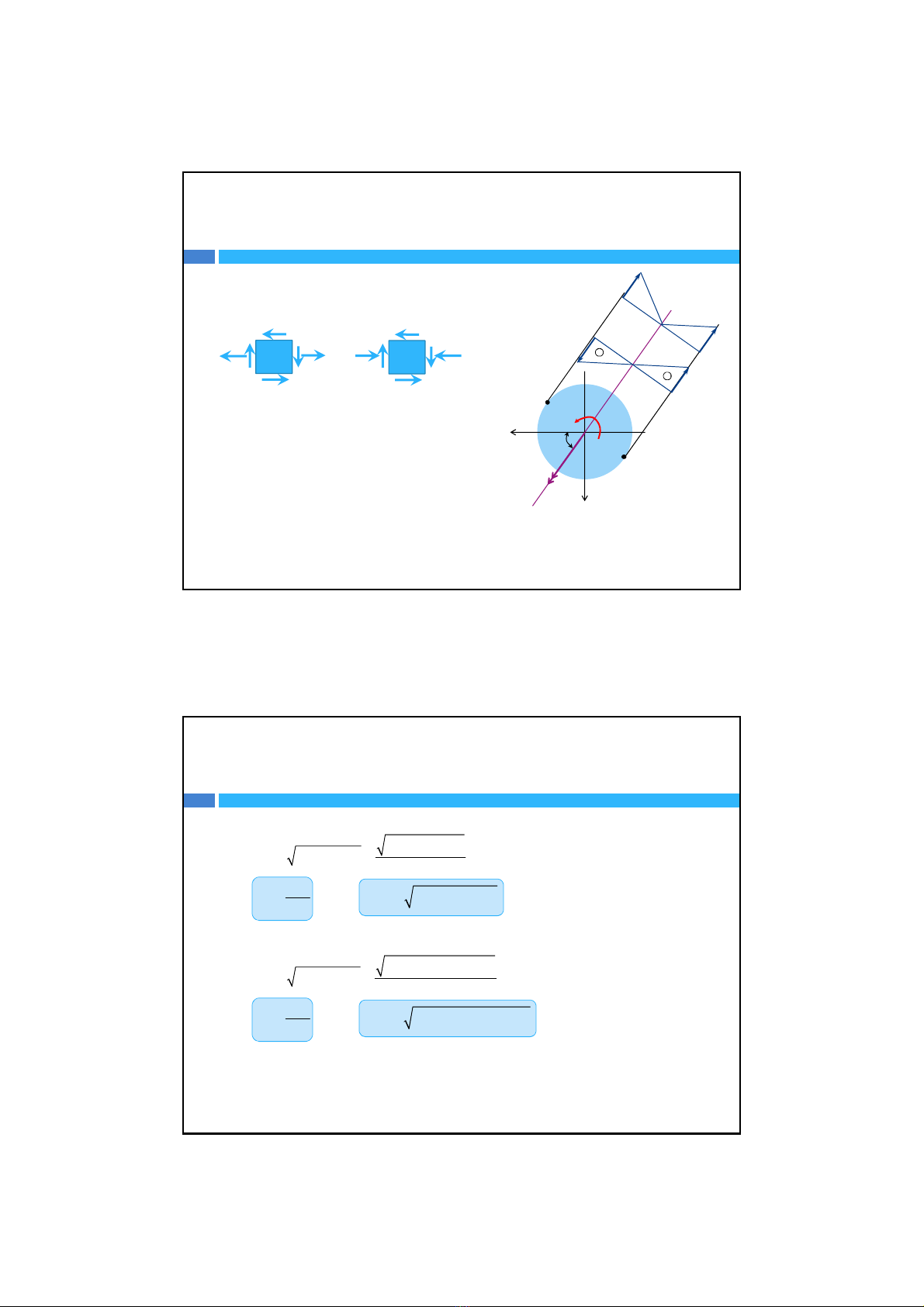
IV‐Thanh chịuuốnxoắnđồng thời
Trong trường hợpuốnxoắnđồng thời, để cho đơn
giảntachỉkhảo sát thanh có mặtcắtnganglà hình
tròn.
Trên mặtcắt có ba thành phầnnộilựclàmô‐men
Mx,mô‐men Myvà mô‐men xoắnT.Dođótrạng
thái ứng suấttrongthanhcócảthành phầnứng
suất pháp zdo Mxvà Mygâyramàcócảứng suất
tiếpdo mô‐men xoắnTgâyra.
Các điểmtrongthanhởtrạng thái ứng suấtphẳng
đặcbiệt.
Thành phầnứng suất pháp zgây ra bởimô‐men
Mxvà Mylà
y
x
z
xy
M
M
y
x
J
J

M
x
y
trục trung hòa
,maxn
,maxk
+
-
tan y
x
M
M
CHƯƠNG 5 Tính bềncácbàitoánthuộcdạng thanh
3. Tính bềncácbàitoánthuộcdạng thanh
Thành phầnứng suấttiếpgây ra bởimô‐men xoắnT
O
T
J

R
Ta nhậnthấyrằng, vớimặtcắthìnhtròn,tạiđiểmcó
bán kính bằng R thì ứng suấtphápvàứng suấttiếp
cùng đạtgiátrịlớnnhất.
Ứng suất pháp kéo và nén lớnnhất
22
max
x
y
u
z
uu
M
M
M
WW
 3
0,1
xyu
WWW D
Với
Ứng suấttiếplớnnhất
max
OO
TT
R
J
W
 3
0, 2
O
WD
Với
Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 10
11/22/2011
Giảng viên Nguyễn Duy Khương 5
CHƯƠNG 5 Tính bềncácbàitoánthuộcdạng thanh
3. Tính bềncácbàitoánthuộcdạng thanh
M
x
y
trục trung hòa
,maxn
,maxk
+
-
max
max
Hai điểmN
+và N‐ởtrạng thái ứng suất
phẳng đặcbiệt.
T
N‐min
max
N+max
max
N
N
Để xác định điềukiệnbềntaphảitính
ứng suấttương đương theo hai thuyết
bền 3 và thuyếtbền4.
CHƯƠNG 5 Tính bềncácbàitoánthuộcdạng thanh
3. Tính bềncácbàitoánthuộcdạng thanh
Thuyếtbềnứng suấttiếplớnnhất(TB3)
222
22
max max
4xy
td
x
M
MT
W



td
td
x
M
W
 Với222
td x y
M
MMT
Thuyếtbềnthếnăng biếnđổihìnhdạng (TB4)
22 2
22
max max
0, 75
3xy
td
x
M
MT
W



td
td
x
M
W
 Với22 2
0, 75
td x y
M
MM T
