Department of Mechatronics/Applied Mechanics - School of Mechanical Engineering
Cơhọckỹthuật
ĐỘNGLỰCHỌC
EngineeringMechanics
KINETICS
ĐỘNG LỰC HỌC
VẬT RẮN KHÔNG GIAN
PHẦN BÀI TẬP
Biên soạn: Bộ môn Cơ học ứng dụng
GV: …………………………………..
Department of Mechatronics/Applied Mechanics - School of Mechanical Engineering 2
MỘT SỐ CHỦ ĐỀ
1. Mômen quán tính khối của vật rắn. Ma trận mômen
quán tính.
2. Mômen động lượng của vật đối với một điểm.
3. Động năng của vật rắn.
4. Phản lực ổ trục vật quay.
5. Gyroscope – hiệu ứng Gyroscope.
Department of Mechatronics/Applied Mechanics - School of Mechanical Engineering 3
1. Mômen quán tính khối – Ma trận mômen quán tính khối
22
22
22
(),
(),
()
xx
yy
zz
Iyzdm
Ixzdm
Ixydm






,
,
xy yx m
xz zx m
yz zy m
II xydm
II xzdm
II yzdm






[,, ]
0
0
0
T
xyz
zy
zx
yx
=
éù
-
êú
êú
=-
êú
êú
-
êú
ëû
u
u




x
y
z
O
x
y
z
dm
u
r
22
22
22
xx xy xz
OOxyz yxyyyz
zx zy zz
B
III
III dm
III
y z xy xz
xy x z yz dm
xz zy x y
éù
êú
êú
º= =-
êú
êú
êú
ëû
éù
+- -
êú
êú
=- + -
êú
êú
-- +
êú
ëû
ò
ò
II uu


 
 
Department of Mechatronics/Applied Mechanics - School of Mechanical Engineering 4
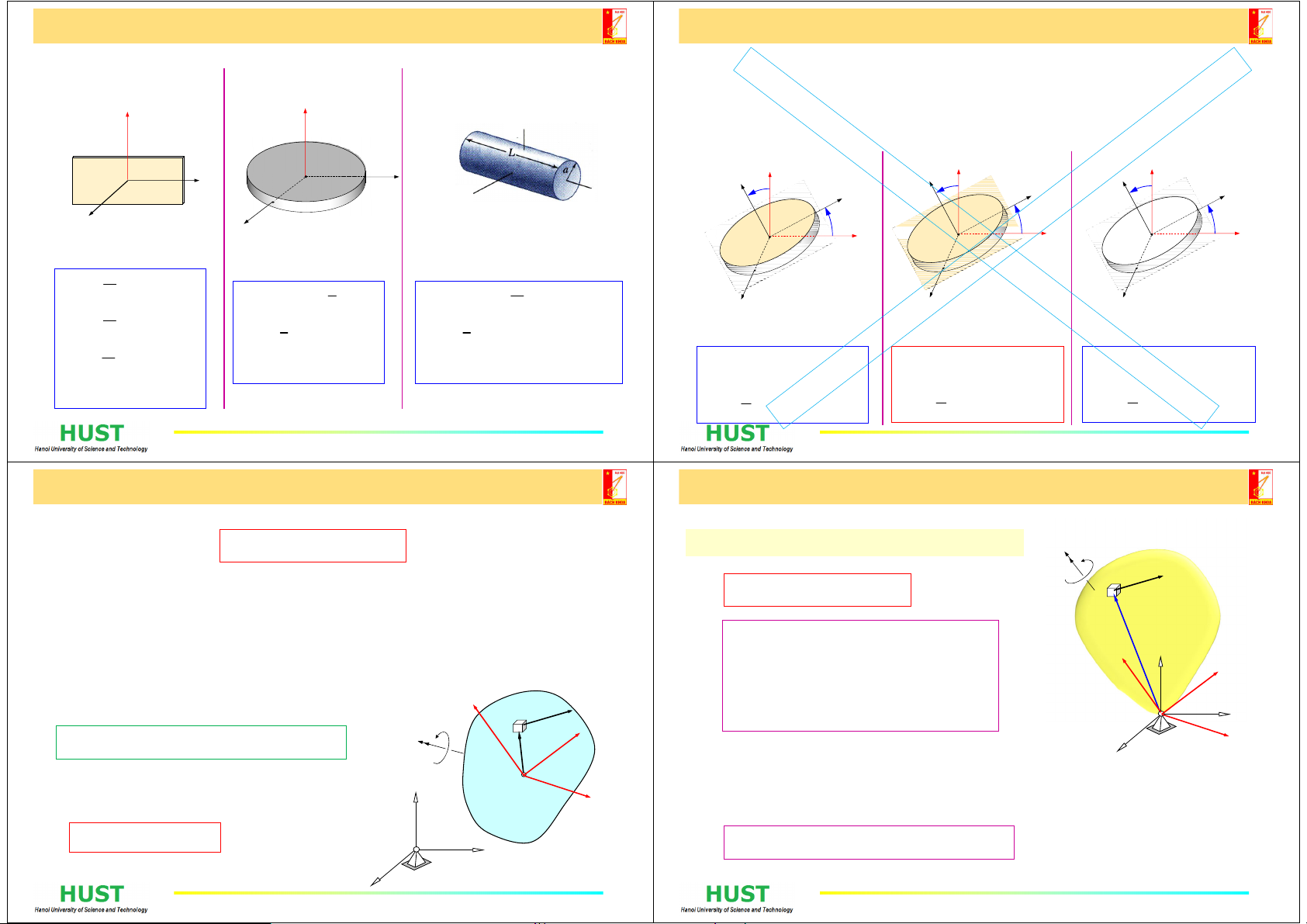
1. Mômen quán tính khối – Ma trận mômen quán tính khối
222
222
222
()
()
()
xCx xCx CC
yCy yCy CC
zCz z Cz CC
II mdI myz
II mdI mxz
II mdI mxy
 
 
 
xy x y C C
yz y z C C
xz x z C C
II mxy
II myz
II mxz






xy
z
O
C
d
r’
r
C
x
C
y
y
z
x
dm
Định lý Huygens-Steiner 1
Định lý Huygens-Steiner 2
Khi xyz là các trục
quán tính chính: 00
00
00
xx
OOxyz yy
zz
I
I
I
éù
êú
êú
º=
êú
êú
êú
ëû
II
Department of Mechatronics/Applied Mechanics - School of Mechanical Engineering 5
1. Mômen quán tính khối – Ma trận mômen quán tính khối
22
1
12
2
1
2
(3 )
0
xx yy
zz
xy yz zx
II mrL
Imr
III
== +
=
===
z
y
x
Cy
x
z
z
C
y
x
b
a
Z tấm
2
1
4
2
1
2
0
xx yy
zz
xy yz zx
II mr
Imr
III
==
=
===
2
1
12
2
1
12
22
1
12 ()
0
xx
yy
zz
xy yz zx
Imb
Ima
Imab
III
=
=
=+
===
Tấm mỏng
(chữ nhật)
Đĩa tròn mỏng Trụ đặc
Department of Mechatronics/Applied Mechanics - School of Mechanical Engineering 6
1. Mômen quán tính khối – Ma trận mômen quán tính khối
Công thức xoay trục hay gặp
Hai hệ trục Oxyz và Ox’y’z’ có cùng gốc và x=x’, trong đó x’y’z’ là hệ trục quán tính
chính. Hệ xyz quay góc quanh x (=x’) thì trùng hệ trục x’y’z’. (lưu ý chiều quay
dương).
y
z
x’
O
y’
x
z’
0
1()sin2
2
xy xz
yz y z
II
IIIb
¢¢
==
=-
0
1()sin2
2
zx zy
xy x y
II
IIIb
¢¢
==
=-
Nếu quay quanh trục z (=z’):
x
y
z’
O
x’
z
y’
Nếu quay quanh trục y (=y’):
0
1()sin2
2
yx yz
xz z x
II
IIIb
¢¢
==
=-
Nếu quay quanh trục x (=x’):
z
x
y’
O
z’
y
x’
Department of Mechatronics/Applied Mechanics - School of Mechanical Engineering 7
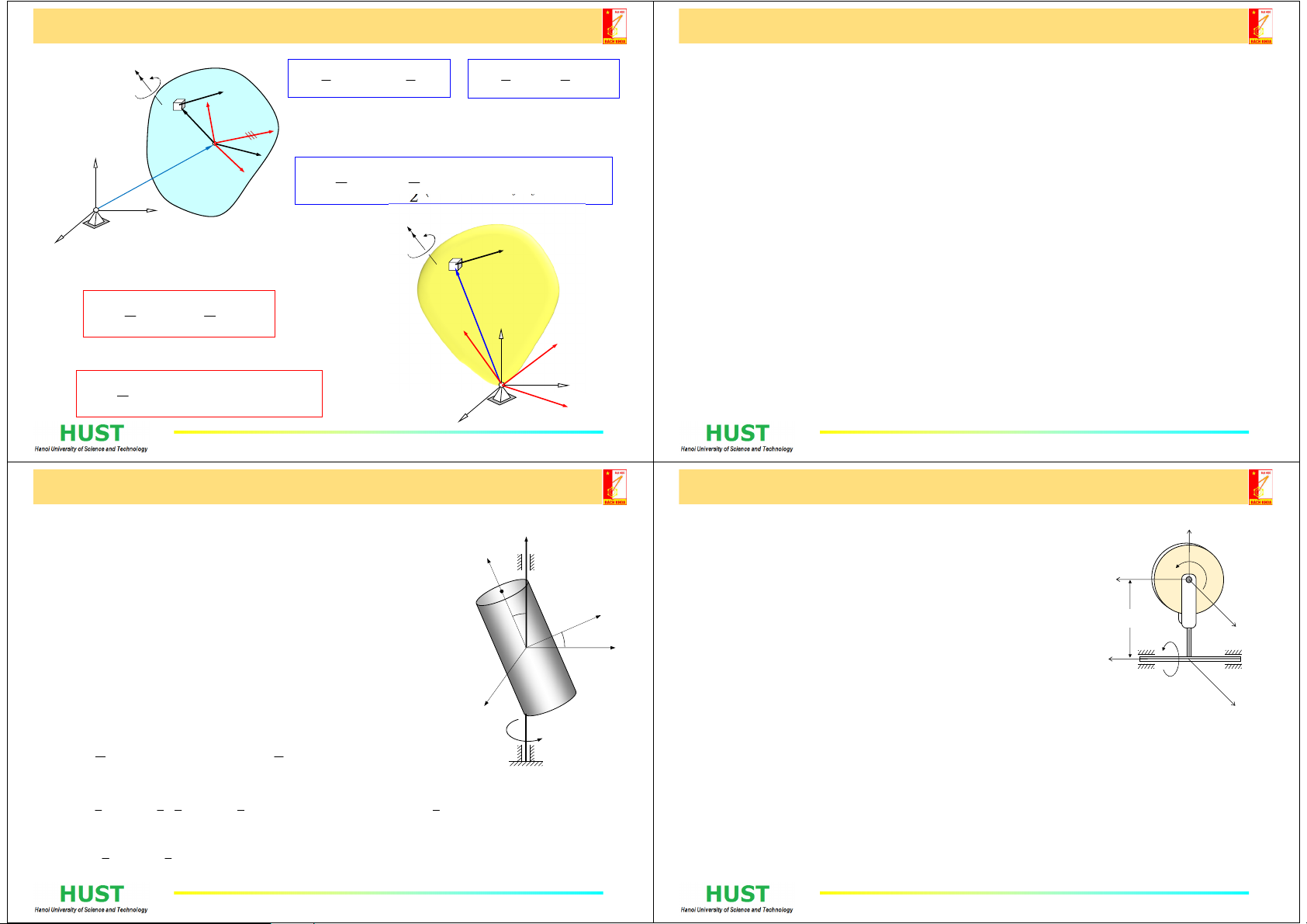
2. Mômen động lượng của vật rắn đối với 1 điểm
xy yz zx
III0===
()
()
()
Cxxxyyyzzz
lIeIeIewww=++

Nếu chọn Cxyz là hệ trục quán tính chính:
x
e
z
e
y
e
C
P
O
vdm
w
u
()
()()
Cxxxyyxzzx
yx x y y yz z y zx x zy y z z z
lI I Ie
IIIeIIIe
www
ww w w ww
=++
+++ +++

CCxxCyyCzz
llelele=++

Đối với khối tâm C
Đối với điểm O
OC CC
lrmvl=´ +
Department of Mechatronics/Applied Mechanics - School of Mechanical Engineering 8
2. Mômen động lượng của vật rắn đối với 1 điểm
Nếu chọn Oxyz là hệ trục quán tính chính:
xy yz zx
III0===
()
()
()
Oxxxyyyzzz
lIeIeIewww=++

P
vdm
w
O
r
x
e
z
e
y
e
Trường hợp vật quay quanh điểm O cố định
()
()
()
Oxxxyyxzzx
yx x y y yz z y
zx x zy y z z z
lI I Ie
IIIe
IIIe
www
ww w
www
=++
+++
+++
OOxxOyyOzz
llelele=++

Department of Mechatronics/Applied Mechanics - School of Mechanical Engineering 9
3. Động năng của vật rắn
Nếu hệ Cxyz gắn liền vật là hệ trục quán tính
chính trung tâm:
11
22
CC C
Tvmv lw=⋅+⋅
Đối với vật rắn quay quanh điểm O cố định:
Nếu hệ gắn liền vật Oxyz là hệ trục quán tính chính
11
22
T
OO
Tl Iw=⋅=
()
222
1
2Ox x Oy y Oz z
TI I Iwww=++
()
2222
11
22
CCxxCyyCzz
Tmv I I Iwww=+ ++
2
11
22
T
CC
Tmv I=+
P
vdm
w
O
r
x
e
z
e
y
e
C
dm
O
v
w
C
r
u
C
v
x
e
z
e
y
e
Department of Mechatronics/Applied Mechanics - School of Mechanical Engineering 10
BÀI TẬP:
Mômen động lượng của vật đối với một điểm
Động năng của vật rắn
Department of Mechatronics/Applied Mechanics - School of Mechanical Engineering 11
Bài 17-2. Mômen động lượng và động năng vật rắn
Khối trụ tròn đồng chất khối lượng m, bán kính R, chiều
dài h quay quanh trục thẳng đứng với vận tốc góc . Hệ
Cxyz gắn vào trụ, trục đối xứng z tạo với trục quay góc ,
có các véc tơ đơn vị là [i, j, k].
•Tính véctơ mômen động lượng của vật đối với gốc tọa
độ O, biểu diễn theo [i, j, k].
•Tính động năng từ đó suy ra mômen quán tính khối
của vật đối với trục quay.
22 2
222 222 2
1111 1
0
2243 2
222 22
11
043
11
(/3)sin cos
42
[( ) sin 2 cos ]
[( ) sin 2 cos ]
C
O z
z
lmrh jmr k
Tl mrh r I
Imrh r







x
C
z
y
B
A
z0
Department of Mechatronics/Applied Mechanics - School of Mechanical Engineering 12
Bài 17-5. Mômen động lượng và động năng vật rắn
Đĩa có khối lượng m = 2,72 kg, bán kính r = 10,2 cm,
quay riêng quanh trục qua tâm C với vận tốc góc p =
40 rad/s. Tay quay OC = d = 25,4 cm quay quanh trục x
với vận tốc = 10 rad/s. Hãy xác định:
a) Véctơ động lượng, mômen động lượng của đĩa đối
với điểm C và động năng của đĩa.
b) Véctơ mômen động lượng của đĩa đối với điểm O.
p
ij


222
0,221 1,768 kgm /s; 200, 8 kgm /s
C
lij T

2
5, 735 1, 768 kgm /s
O
lij

d
C
O
p
y
x
z, z’
x’
y’
Department of Mechatronics/Applied Mechanics - School of Mechanical Engineering 13
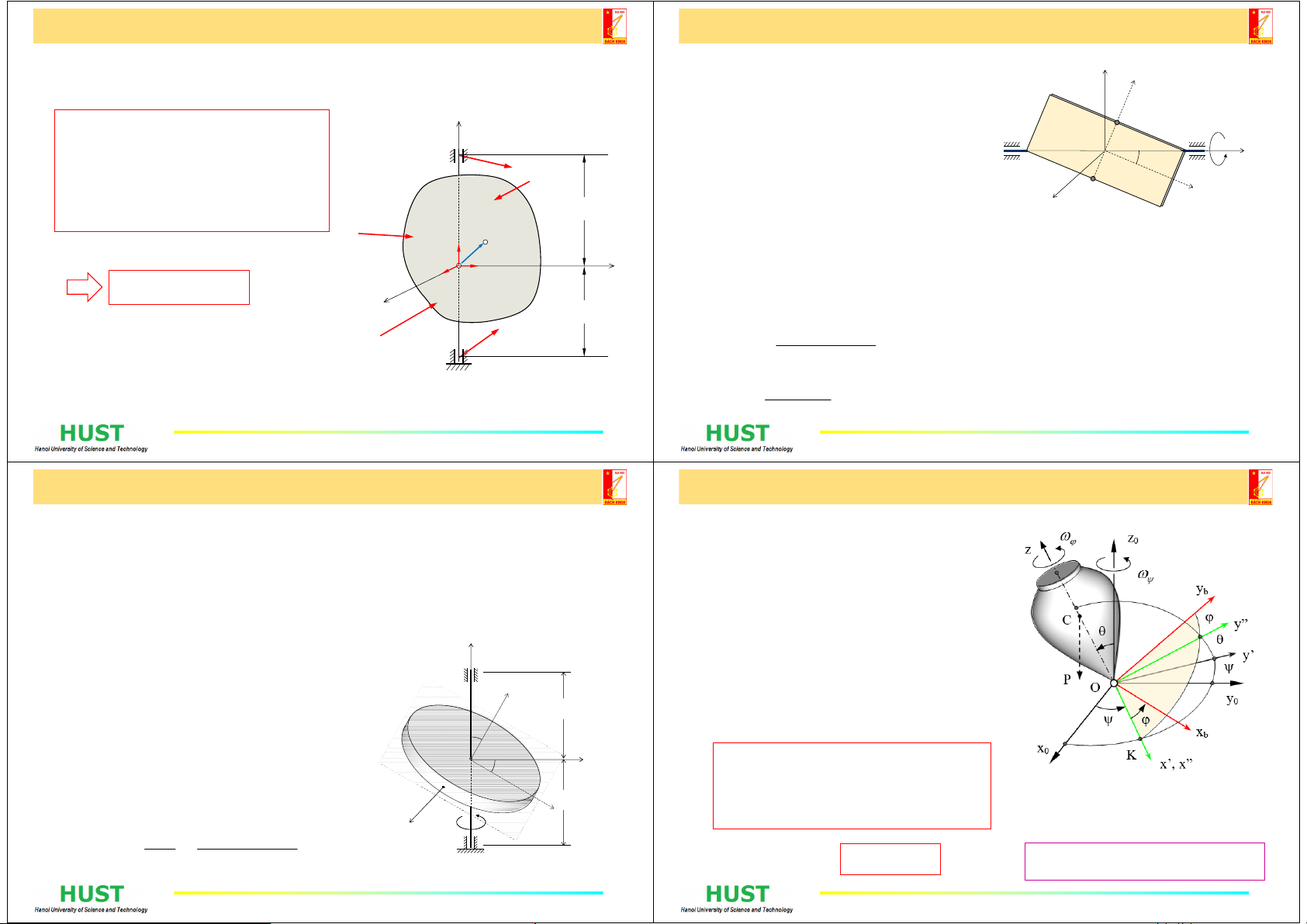
4. Phản lực động phụ tại ổ trục
Các thành phần phản lực động ổ trục được xác định từ
các phương trình sau:
2
2
2
2
()
()
Ax Bx Cz Cz
Ay By C z C z
Ay By xz z yz z
Ax Bx yz z xz z
RRmy x
RRmx y
aR bR I I
aR bR I I
ww
ww
ww
ww
+=--
+= -
-= -
-+ = +
Ax Ay Bx By
RRRR,,,
phản lực động ổ trục
1
F
2
F
n
F
B
R
A
R
z,z0
O
i
j
k
x
y
A
B
b
a
C
C
s
Department of Mechatronics/Applied Mechanics - School of Mechanical Engineering 14
Bài 17-9. Xác định phản lực ổ trục
Tấm đồng chất hình chữ nhật có các
cạnh dài là a và cạnh ngắn là b, khối
lượng m, quay đều quanh đường chéo
AB với vận tốc góc .
a) Xác định áp lực động lên hai ổ đỡ
A, B.
b) Để làm triệt tiêu các phản lực động
phụ tại ổ trục, người ta gắn hai khối
lượng m1 vào điểm D và E, xác
định m1.
z
x
y’, y
O
AB
x’
z’
E
D
b
222
2 2 3/2
()
;;0;
12( )
ddddd
ABAAB
mab a b
XXXYY
ab
 
12
2( )
xz
II
mb

Department of Mechatronics/Applied Mechanics - School of Mechanical Engineering 15
Đĩa tròn đồng chất bán kính R, khối lượng m được gắn cứng với trục đứng AB
đi qua khối tâm O. Đĩa quay đều với
quanh trục AB. Trục đối xứng z’
(vuông góc với đĩa) nghiêng với trục quay AB một góc . Cho các khoảng
cách AO = OB = h. Tính phản lực động lực tại các ổ trục A và B.
Bài 17-11. Xác định phản lực ổ trục
22
sin 2
16
qt
dd O
AB
Mmr
YY AB h

x
z
z’
O
x’
A
y’
y
B
h
h
Department of Mechatronics/Applied Mechanics - School of Mechanical Engineering 16
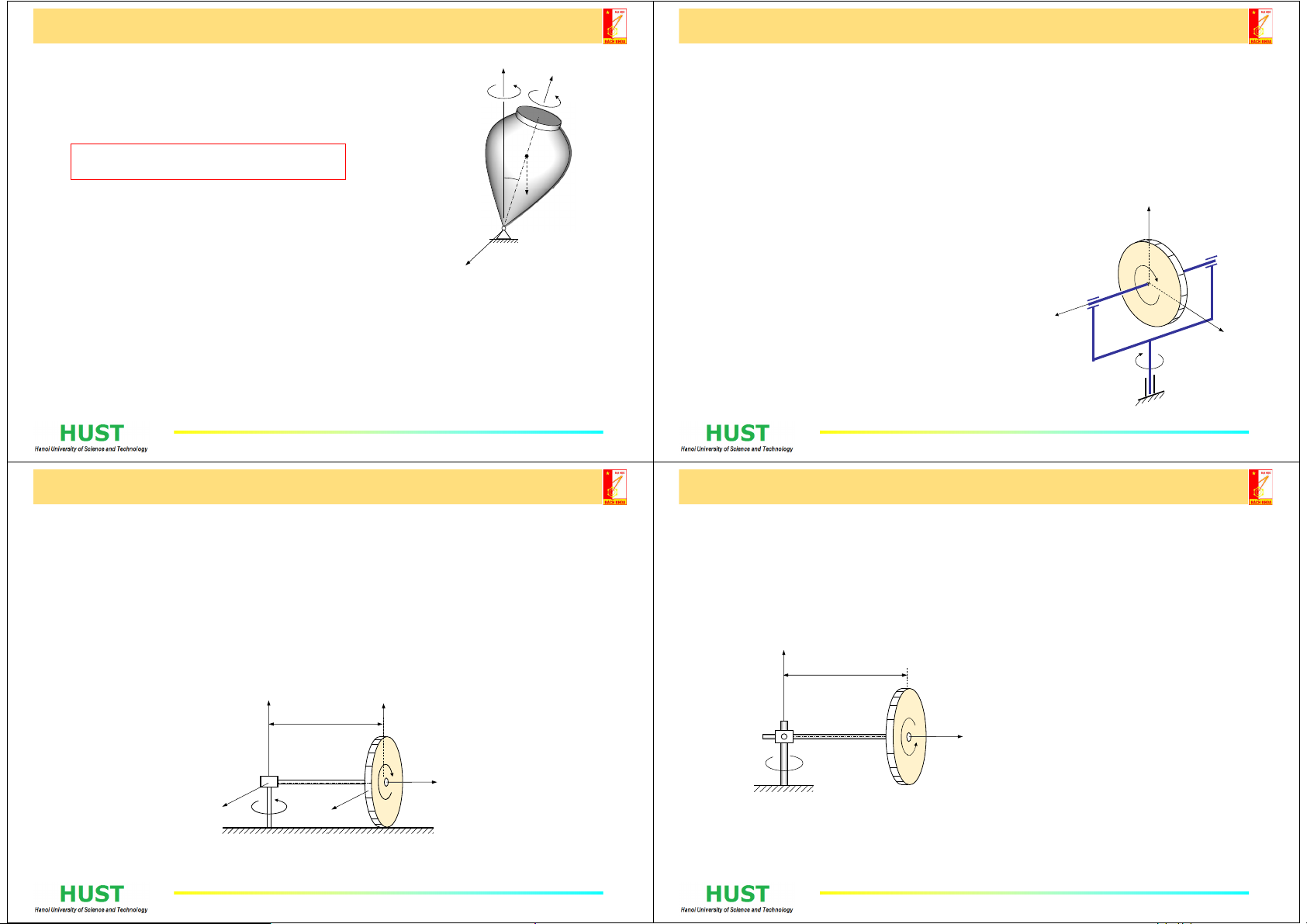
5. Mômen Gyroscope
Gyroscope là vật rắn đồng chất có trục đối
xứng động lực quay quanh điểm trên trục
đối xứng đó.
Khi tiến động đều: (Sử dụng 3 góc Euler Z-X-Z)
2
212
sin cos sin
sin ( cos )
sin ( cos )
xx zz
zz x
zx
MI I
II
II



 




,,
,0, 0
const const
const




mômen lực quán tính đối với trục x” được tạo ra
Khi =90:21xz
MI
 Ví dụ: z là trục đối xứng động lực nếu nó
là trục quán tính chính trung tâm và Ix = Iy.
Department of Mechatronics/Applied Mechanics - School of Mechanical Engineering 17
5. Mômen Gyroscope
O
z0z
1
P
C
2
x
12 12
qt
gy O z
MMI


 
Công thức gần đúng tính mômen con quay
(mômen Gyroscope)
Công thức này đúng khi = 90.
Department of Mechatronics/Applied Mechanics - School of Mechanical Engineering 18
Bài 17-17. Hiệu ứng Gyroscope - phản lực ổ trục
Rôto là một đĩa tròn đồng chất khối lượng m, bán kính r, quay quanh trục đối
xứng AB nằm ngang với vận tốc góc
1. Trục AB lại quay quanh trục thẳng
đứng z0 qua khối tâm O của đĩa với vận tốc góc
2. Cho biết OA = OB = h.
a) Xác định mômen động lượng lO, động năng T của con quay.
b) Phản lực toàn phần tại hai ổ A và B, có thể sử dụng một ổ đỡ được không,
ổ nào và khi nào?
z
y
x
1
2
O
A
B
Department of Mechatronics/Applied Mechanics - School of Mechanical Engineering 19
Bài 17-18. Hiệu ứng Gyroscope - phản lực
z
O
b
A
2 C
x
y
1
Cho đĩa đồng chất bán kính r, khối lượng m được lắp với tay quay OC = b nằm
ngang như hình vẽ. Khi OC quay xung quanh trục thẳng đứng với vận tốc góc
2 = const làm đĩa lăn không trượt trên nền cố định. Bỏ qua trọng lượng tay
quay OC. Hãy xác định:
a) Mômen động lượng của đĩa đối với điểm O, lO .
b) Hãy xác định lực liên kết của nền đặt vào đĩa và lực liên kết tại ổ trục O.
Department of Mechatronics/Applied Mechanics - School of Mechanical Engineering 20
Bài 17-18’. Hiệu ứng Gyroscope
z
x
O
b
C
1
2
Đĩa tròn có khối lượng m, mômen quán tính đối với trục đối xứng z là Iz. Tay
quay OC chiều dài b. Đĩa quay nhanh quanh trục z với vận tốc góc 1. Xác định
chuyển động của OC (độ lớn và chiều quay 2) để OC nằm ngang.