Nguyen Quang Hoang - Department of Mechatronics/Applied Mechanics -1-
PHƯƠNG TRÌNH LAGRANGE LOẠI 2
Lagrange's Equations of Second Kind
Nguyễn Quang Hoàng
Email: hoang.nguyenquang@hust.edu.vn
Nguyen Quang Hoang - Department of Mechatronics/Applied Mechanics -2-
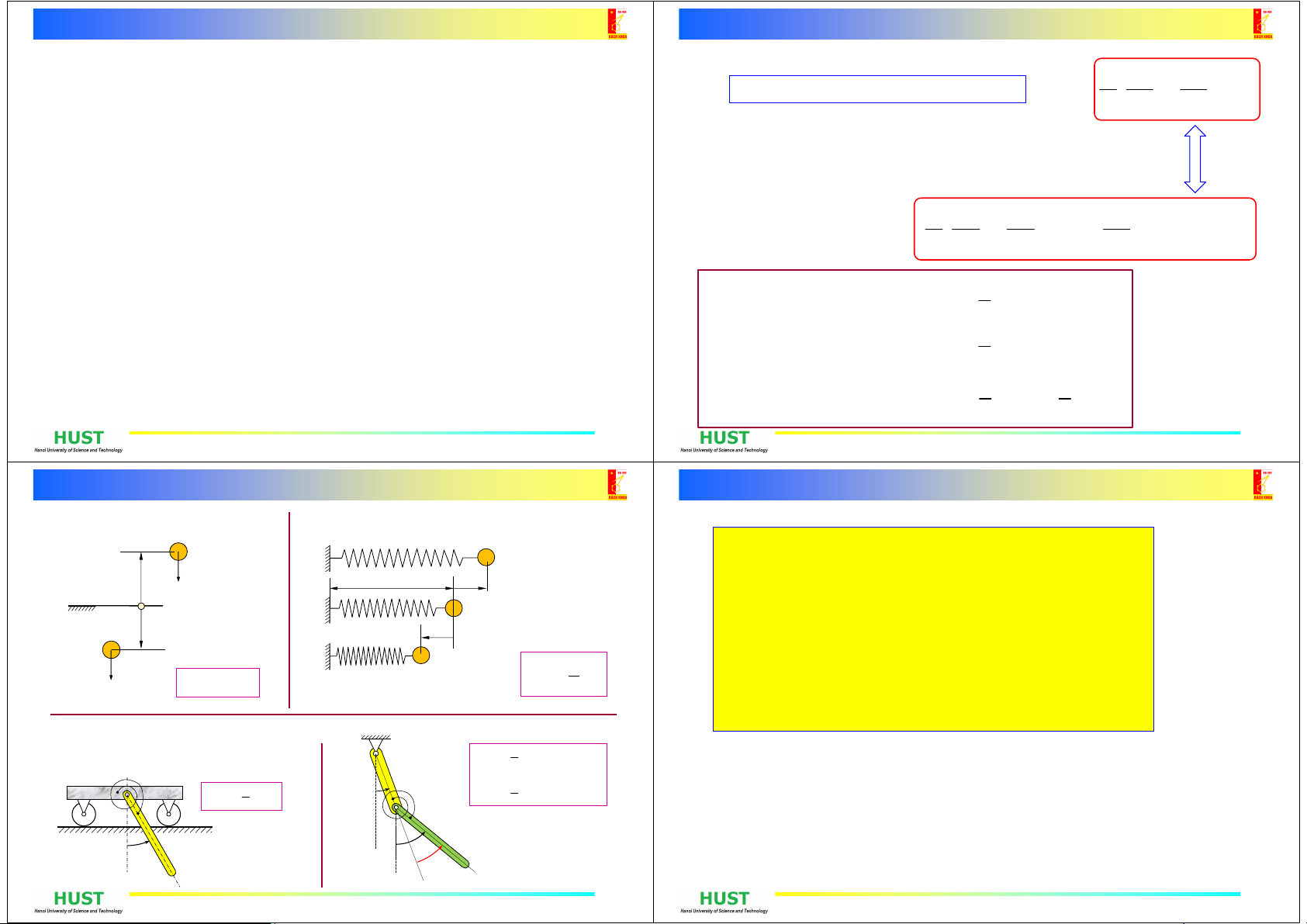
Phương trình Lagrange loại 2
11 1
( ,..., , ,..., , ) ( ,..., )
f
ff
LTqqqqt qq=-P

HàmLagrangecủahệ
làbiểuthứcđộngnăng
làbiểuthứcthếnăngcủahệ
1
( ,..., )
f
qqP
11
( ,..., , ,..., , )
f
f
Tq q q q t

kt
i
ii
dL L
Q
dt q q
æö
¶¶
÷
ç÷-=
ç÷
ç÷
綶
èø
, ( 1,2,..., )
kt
i
ii i
dT TQif
dt q q q
æö
¶¶ P
÷
ç÷-=- =
ç÷
ç÷
綶
èø
Động năng
Vậtrắntịnh tiến
Vậtrắn chuyểnđộng phẳng
Vậtrắnqqtrụczcốđịnh
2
1
2C
Tmv=
2
1
2z
TIw=
22
11
22
CCz
Tmv Iw=+
Nguyen Quang Hoang - Department of Mechatronics/Applied Mechanics -3-
Thế năng của trọng lượng và lò xo tuyến tính
yW
g=0
g=+Wy
g=‐Wy
‐y
W
k
l0s
s
=0
=ks2/2
=ks2/2
gmgyP= 2
1
2
eksP=
Thếnăngcủalòxoxoắn
1
2
k
k
ThếnăngcủatrọnglựcThếnăngcủalòxokéonén
2
1
2
kjP=
2
1
2
2
1
21
2
()
k
k
q
jj
P=
=-
Nguyen Quang Hoang - Department of Mechatronics/Applied Mechanics -4-
Phương trình Lagrange loại 2
Các bướcthựchiệnkhiápdụng:
1. Xác định sốbậctựdo củahệ;
2. Chọntọađộ suy rộng đủ;
3. Tính biểuthứcđộng năng và thếnăng hệ;
4. Tính lựcsuyrộng củacáclực/ngẫulực không thế;
5. Tính các đạohàm;
6. Viếtphương trình Lagrange loại2chohệ.
Nguyen Quang Hoang - Department of Mechatronics/Applied Mechanics -5-
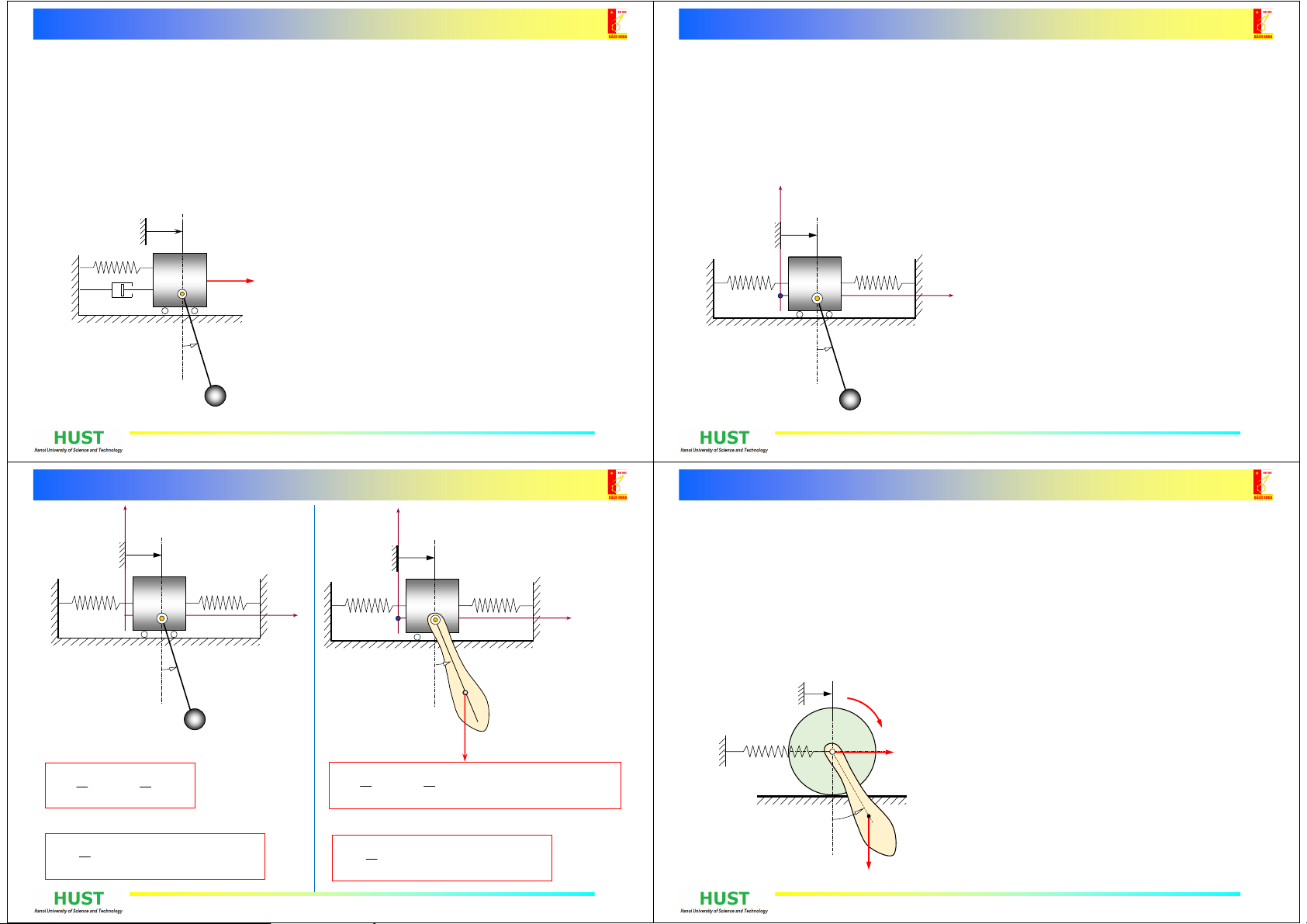
PT Lagrange loại 2 - Ví dụ
x
k
m1
c
F(t)
m2
l
B
A
Môhìnhcầutrụccùngvớitảitrọngđượcchonhưhìnhvẽ.XeAcókhối
lượngm1chuyểnđộngtrênđườngngang,lòxocóđộcứngk,cảnnhớt
hệsốc.DâyABcóchiềudàil,khốilượngkhôngđángkểvàluôncăng.Tải
trọngBđượccoinhư chấtđiểmcókhốilượngm2.Thiếtlậpphương
trìnhviphânchuyểnđộngvớicáctọađộsuyrộngxvà:
Nguyen Quang Hoang - Department of Mechatronics/Applied Mechanics -6-
Bài tập 16-3
Vật A có khốilượng m1đượcnốivớicácđường cốđịnh nhờcáclòxocó
độ cứng nhưnhau k,cóthểtrượt không ma sát dọc sàn ngang. Quảcầu
nhỏBkhốilượng m2được treo vào thanh mảnh, nhẹ,chiều dài l,vànối
bảnlềtại A. Thành lậpphương trình vi phân chuyểnđộng củahệvà tìm
các tích phân đầu.
x
k1m1
m2
l
B
A
k2
x
y
Phân tích chuyển động:
Số bậc tự do
Tọa độ suy rộng
Dạng chuyển động
Lực sinh công (có thế và
không thế)
Nguyen Quang Hoang - Department of Mechatronics/Applied Mechanics -7-
Bài tương tự

222
1222
11 ,
22


ACC
Tmv mvI
2
12 2
1() cos;
2
 kkx mgl
x
k1m1
m2, IC
l = AC
B
A
k2
x
y
C
x
k1m1
m2
l
B
A
k2
x
y
22
12
11
,
22

A
B
Tmv mv
2
12 2
1() cos;
2
 kkx mgl
Nguyen Quang Hoang - Department of Mechatronics/Applied Mechanics -8-
Bài tập 16-17
Cho cơhệchuyểnđộng trong mặtphẳng thẳng đứng nhưtrên hình. Đĩađồng chất
tâm A khốilượng m1, bán kính R,lăn không trượttrênnền ngang. Con lắcABtrọng
lượng Q=m2gvà khốitâmCvớiAC = l, mômen quán tính khốiđốivớitrục qua
khốitâmClàIC,đượcnốivàoAbằng mộtkhớpbảnlềtrụ.TrênđĩacóngẫulựcM
và lựcFnằm ngang tác dụng. Hãy thiếtlậpphương trình vi phân chuyểnđộng của
hệ.
A
M
x
k
C
Q
B
F
Phân tích chuyển động:
Số bậc tự do
Tọa độ suy rộng
Dạng chuyển động
Lực sinh công (có thế và
không thế)
Nguyen Quang Hoang - Department of Mechatronics/Applied Mechanics -9-
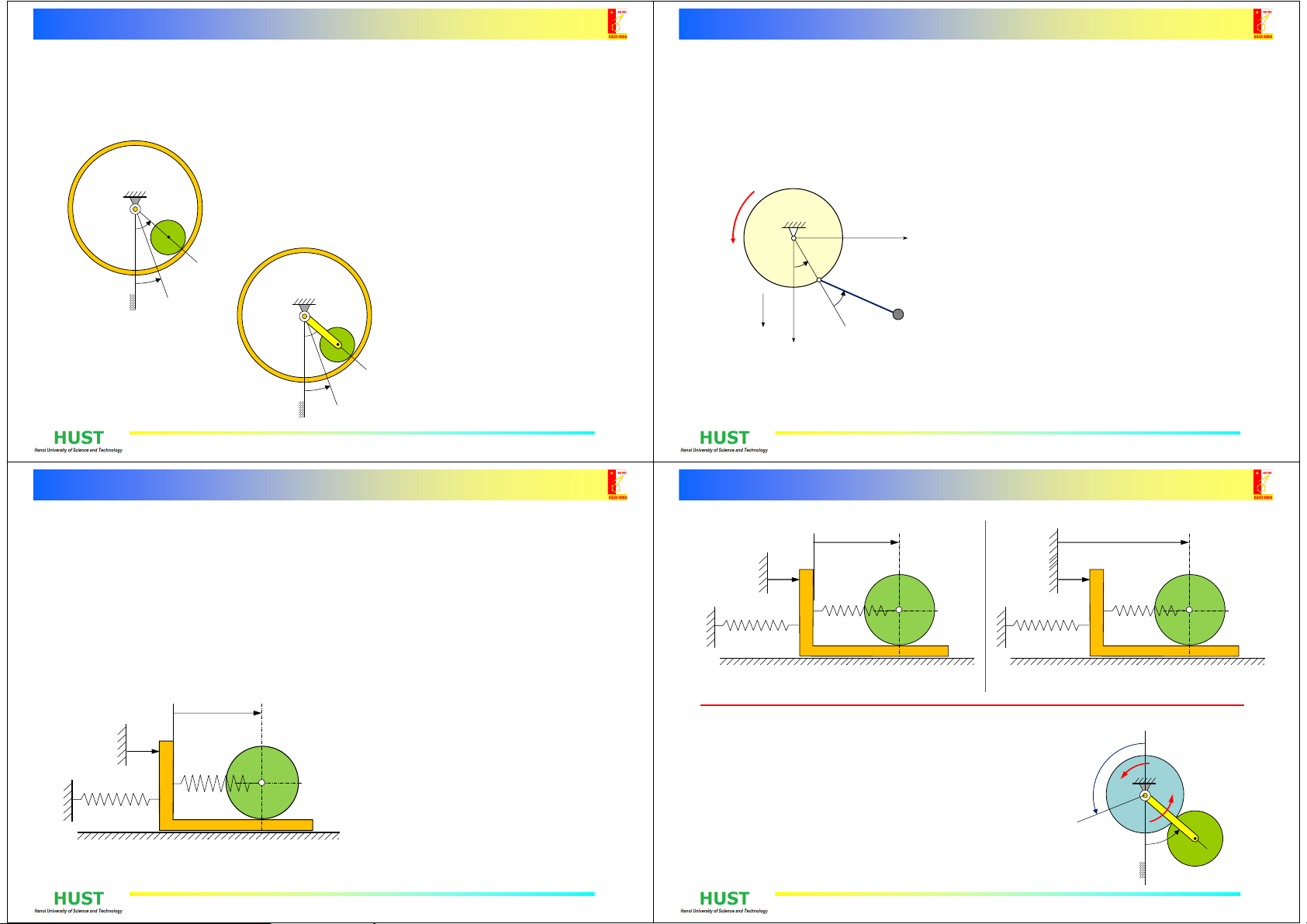
Bài tập 16-6
Phân tích chuyển động:
Số bậc tự do
Tọa độ suy rộng
Dạng chuyển động
Lực sinh công (có
thế và không thế)
Mộthìnhtrụkhốilượng mbán kính rlănkhôngtrượt bên trong mộttrụrỗng, khối
lượng Mbán kính R.Trụnày có thểquay quanh trụcnằm ngang O. Mômen quán
tính củacáctrụđốivớicáctrụctương ứng bằng MR2và mr2/2. Thành lậpphương
trình vi phân chuyểnđộng củahệvà tìm các tích phân đầu.
O
C
O
C
Nguyen Quang Hoang - Department of Mechatronics/Applied Mechanics -10-
Bài tập 16-7
Mộtđĩađồng chất bán kính R,cókhốilượng Mcó thểquay xung quanh
trụcnằm ngang O. Một dây nhẹkhông giãn AB = l,mộtđầucủanótreo
vào vành đĩatạiA,vàđầukiabuộcvậtcókhốilượng mtạiB(coinhư
chấtđiểm). Thành lậpphương trình vi phân chuyểnđộng củahệ.
x
O
A
g
y
B
M
Phân tích chuyển động:
Số bậc tự do
Tọa độ suy rộng
Dạng chuyển động
Lực sinh công (có thế và
không thế)
Nguyen Quang Hoang - Department of Mechatronics/Applied Mechanics -11-
Bài tập 16-16
Cho cơ hệ như trên hình vẽ. Con lăn tâm C là trụ tròn đồng chất, khối lượng m2,
lăn không trượt trên tấm A. Tấm A có khối lượng m1, chuyển động không ma sát
trên nền ngang. Các lò xo có độ cứng lần lượt là k1 và k2. Khi x1 = 0 và x2 = l các
lò xo không biến dạng. Chọn tọa độ suy rộng cho hệ là x1 và x2. Thiết lập phương
trình vi phân chuyển động của cơ hệ và tìm các tích phân đầu.
x1
x2
C
k1
k2
A
Phân tích chuyển động:
Số bậc tự do
Tọa độ suy rộng
Dạng chuyển động
Lực sinh công (có thế và
không thế)
Nguyen Quang Hoang - Department of Mechatronics/Applied Mechanics -12-
Bài tập tương tự
x1
x2
C
k1
k2
A
x1
x2
C
k1
k2
A
Cho cơcấuvisaichuyểnđộng trong mặtphẳng
ngang. Moment M1tác dụng lên bánh răng 1, M2tác
dụng lên tay quay OA.
Bánh 1: m1,r1,Bánh2:m2,r2,
Tay quay: m0,L=r1+r2.
O
A
Nguyen Quang Hoang - Department of Mechatronics/Applied Mechanics -13-
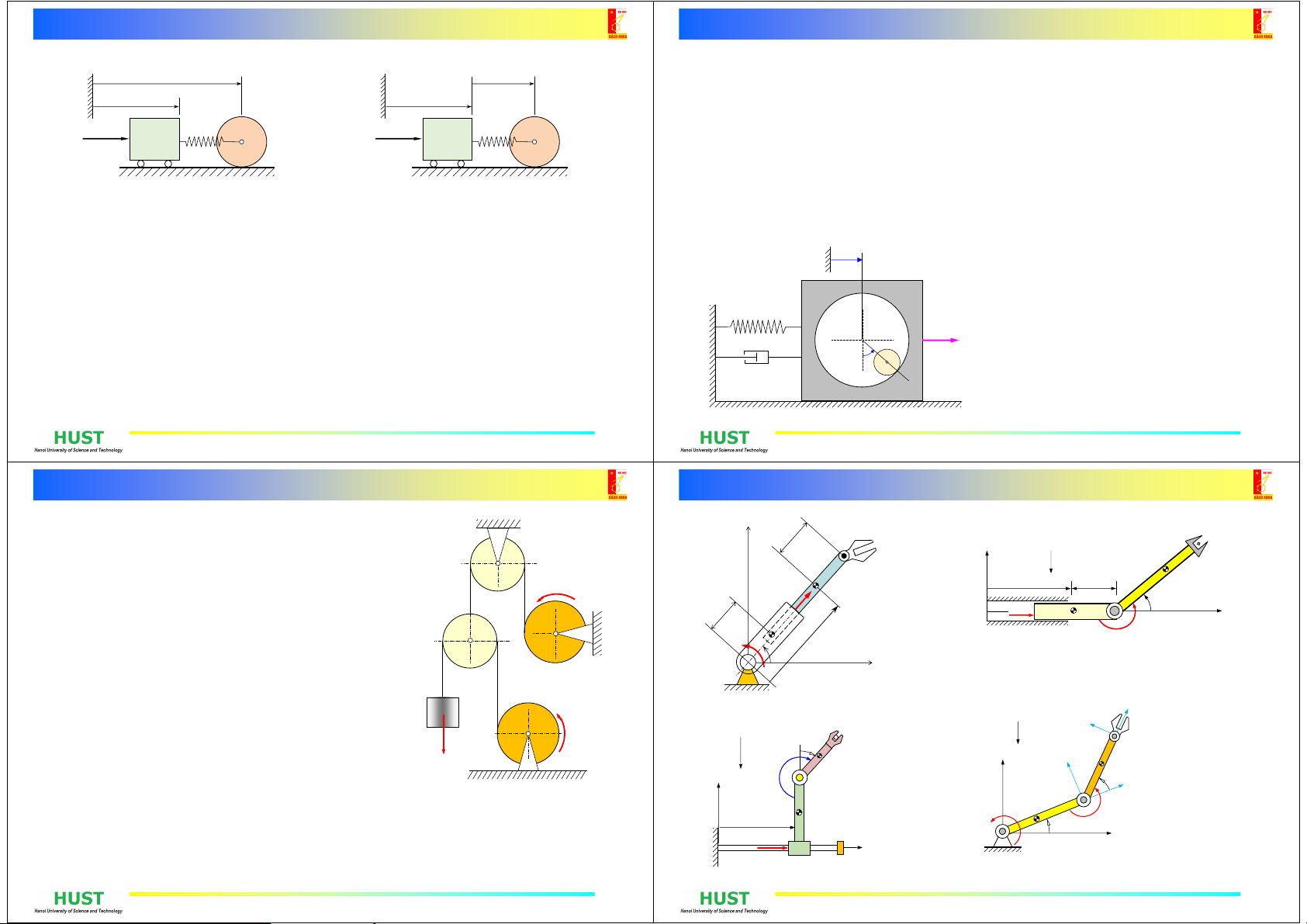
Bài tập tương tự
x1
C
k
A
F(t)
x2
x1
C
k
A
F(t)
x2
Nguyen Quang Hoang - Department of Mechatronics/Applied Mechanics -14-
Bài tập 16-9
Dầm1khốilượng m1được khoét theo chiềudọcmộtrãnhtrụcó bán
kính R,mộthìnhtrụtròn đồng chất 2 bán kính r,khốilượng m2lăn
không trượt trong rãnh. Trục rãnh trụvà trụchìnhtrụ2 song song với
nhau. Dầm 1 chuyểnđộng trên mặtphẳng ngang nhẵndướitácdụng
củalực ngang F(t),lựcđàn hồituyến tính củalòxocóđộ cứng kvà lực
cảntỷlệbậcnhấtvớivậntốccóhệsốcảnb.Hãythiếtlậpphương trình
vi phân chuyểnđộng củahệ.
O
C
k
b
x
M
F(t)
2
1
Phân tích chuyển động:
Số bậc tự do
Tọa độ suy rộng
Dạng chuyển động
Lực sinh công (có thế và
không thế)
Nguyen Quang Hoang - Department of Mechatronics/Applied Mechanics -15-
Bài tập 16-10
VậtAcókhốilượng mđượckéolênnhờcác trục
quay I và II có cùng bán kính Rvà mômen quán
tính của chúng đốivớitrục quay riêng bằng I.Xác
định gia tốccủavậtAnếucáctrụcquaychịutác
dụng củacácngẫulựccómômenlàM1và M2.Bỏ
qua khốilượng của các ròng rọcvàmasátởcác ổ
trục. Coi các dây là nhẹ, không giãn và không
trượtđốivới các ròng rọc.
Q
C
A
M1
M2
II
I
2
1
Phân tích chuyển động:
Số bậc tự do
Tọa độ suy rộng
Dạng chuyển động
Lực sinh công (có thế và không thế)
Nguyen Quang Hoang - Department of Mechatronics/Applied Mechanics -16-
Một số tay máy phẳng 2 bậc tự do
u
O
P
C1
C2
M(t)
F(t)
a
b
x
y
m2, I2z
m1
u1
u2
x
y0
a2
g
C1
C2
A
B
Ox0
d
q1
x0
q2
x1
x2
y2
y1
y0
O1
O0
O2
l1
l2
g
u2
u1
C2
Ox0
q1
q2
u2
u1
y0
E
C1
C2
g
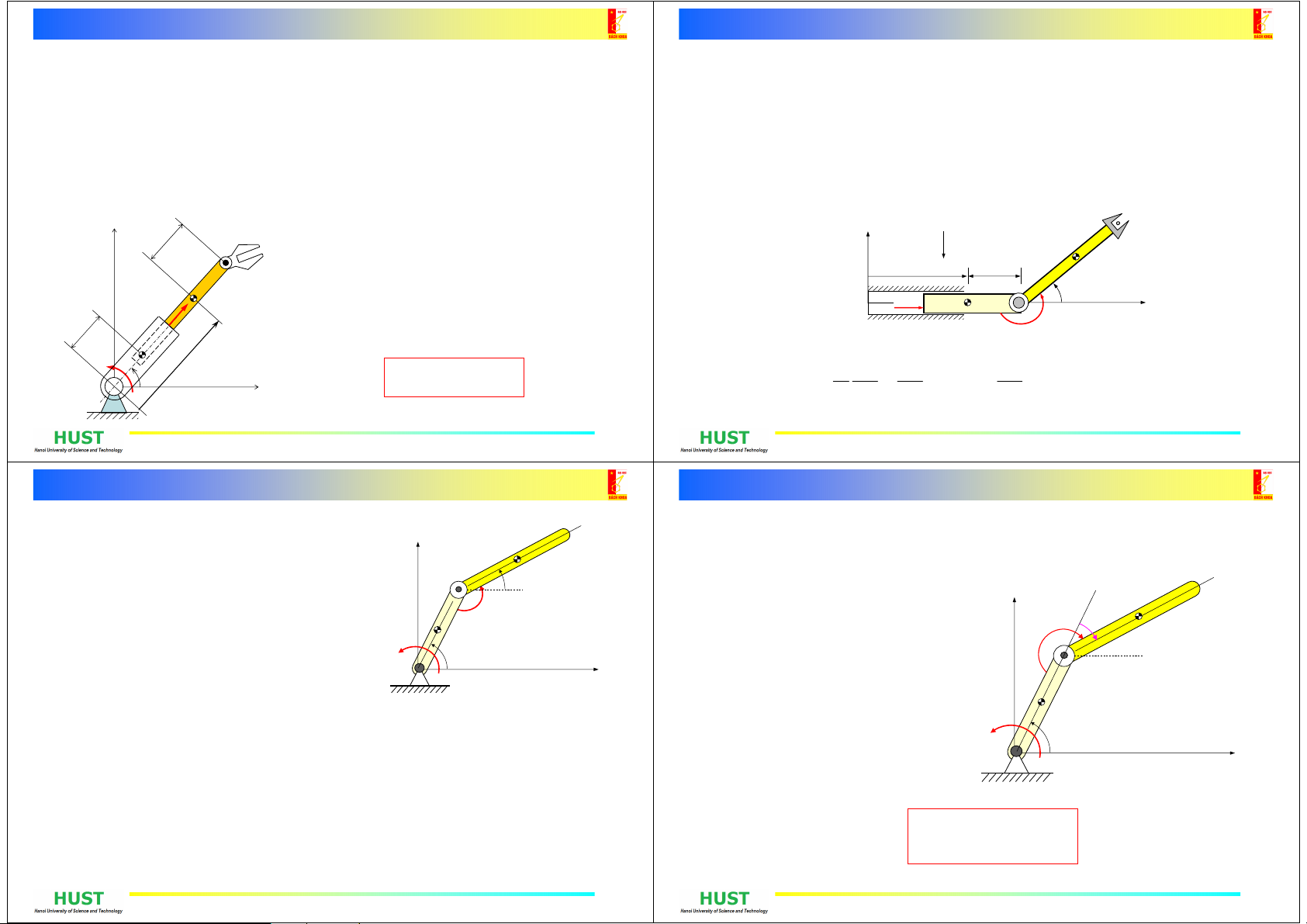
Nguyen Quang Hoang - Department of Mechatronics/Applied Mechanics -17-
Bài tập 16-14
Tay máy chuyển động trong mặt phẳng thẳng đứng. Khâu 1 có khối lượng m1 và
mômen quán tính khối đối với khối tâm C của nó là I1 quay quanh trục ngang qua
O cố định. Khâu 2 có khối lượng m2 và mômen quán tính khối đối với khối tâm
C2 của nó là I2 và chuyển động tịnh tiến đối với khâu 1. Tác dụng một ngẫu lực
điều khiển có mômen M(t) lên khâu quay 1 và một lực điều khiển F(t) lên khâu 2.
Bỏ qua ma sát và lực cản. Viết phương trình chuyển động của tay máy theo các
tọa độ suy rộng
và u.
Phân tích chuyển động:
Số bậc tự do
Tọa độ suy rộng
Dạng chuyển động
Lực sinh công (có thế và không thế)
12


u
O
P
C1
C2
M(t)
F(t)
a
b
x
y
Nguyen Quang Hoang - Department of Mechatronics/Applied Mechanics -18-
Tay máy T-R
Mô hình cơ học của tay máy phẳng hai bậc tự do gồm khâu 1 tịnh tiến theo
phương ngang, khâu hai nối với khâu 1 bằng khớp quay A, khoảng cách C1A= d.
Khâu 1 có khối lượng m1 trượt không ma sát trên nền ngang dưới tác dụng của
lực ngang F1. Khâu 2 có khối lượng m2, khối tâm C2, khoảng cách AC2 = lC2,
mômen quán tính khối đối với trục ngang qua C2 là IC2. Tại khớp quay A có
mômen (nội lực) M2 tác dụng.
,1,2
kt
ii
ii i
dT T QQi
dt q q q
¶¶ P
-==-+ =
¶¶
m2, I2z
m1
u1
u2
x
y0
a2
g
C1
C2
A
B
O
x0
d
Nguyen Quang Hoang - Department of Mechatronics/Applied Mechanics -19-
Tay máy R-R
Tay máy hai bậc tự do chuyển động trong
mặt phẳng thẳng đứng. Khâu 1 chiều dài OA
= l1, khối tâm C1, OC1 = s1, khối lượng m1,
mômen quán tính đối với trục qua khối tâm
là IC1. Khâu 2 chiều dài AB = l2, khối tâm
C2, AC2 = s2, khối lượng m2, mômen quán
tính đối với trục khối tâm là IC2. Động cơ 1
gắn liền với giá cố định tạo ra mômen M1 tác
dụng lên khâu 1, động cơ 2 gắn liền với khâu
1 tạo ra mômen M2 tác dụng lên khâu 1.
B
u2
q1
q2
O
A
C1
C2
u1
x
y
Nguyen Quang Hoang - Department of Mechatronics/Applied Mechanics -20-
Tay máy R-R
Sửdụng PT Lagrange 2 thiếtlập
PT động lựcchotaymáy2bậctự
do chuyểnđộng trong mặtphẳng
đứng.
Khâu 1: m1, L1, IC1, OC1= lC1.
Khâu 2: m2, L2, IC2, AC2= lC2.
11 22
Auq uqddd=+
11
22
kt
kt
Qu
Qu
=
=
11
22
10
01
uu
uu
Bu
éù é ùéù
êú ê úêú
==
êú ê úêú
êú ê úêú
ëû ë ûëû
B
u2
q1
q2
O
A
C1
C2
u1
x
y