Nguyen Quang Hoang - Department of Applied Mechanics
-1-
PHƯƠNG PHÁP NĂNG LƯỢNG
Principles of Work and Energy
Nguyễn Quang Hoàng
Email: hoang.nguyenquang@hust.edu.vn
Nguyen Quang Hoang - Department of Applied Mechanics
-2-
1.CÔNGVÀCÔNGSUẤTCỦALỰC
1.1Côngcủalực
Côngnguyêntố:
F
rdr+
dr
a
MN
x
e
z
e
y
e
x
z
y
O
r
Cônghữuhạn:
cosdA F dr Fds
cos
NN
MM
rs
MN
rs
AFdrFds
- Trường hợp Fcos = const.
MN
AF scos
F
MN
s
-Đơn vị: Nm hoặc Joule (J):
1J = 1Nm
Nguyen Quang Hoang - Department of Applied Mechanics
-3-
1.CÔNGVÀCÔNGSUẤTCỦALỰC
1.2Côngsuấtcủalực
()
() cos .
dA F
WF Fv Fv
dt
Đơn vị của công suất là Watt (W): 1W = 1 J/s
1.3Côngvàcôngsuấtmộtsốlựcthườnggặp
(
)
sin .Amg mgs b=
(
)
sinWmg mgv b=
• Công và công suất của trọng lực
Nguyen Quang Hoang - Department of Applied Mechanics
-4-
1.CÔNGVÀCÔNGSUẤTCỦALỰC
1.3Côngvàcôngsuấtmộtsốlựcthườnggặp
• Công và công suấtcủacủalựcvàngẫulực
là hằng sốtác dụng lên vật quay
() (),
O
AF m F j=() ,AM Mj=
() ();
O
WF m F w=()WM Mw=
k
l0ss
s
Aksdsks
2
00
1
2
-=- =-
ò
dh
Fks
• Công của lực đàn hồi tuyến tính của lò xo
M
O
F
Nguyen Quang Hoang - Department of Applied Mechanics
-5-
1.CÔNGVÀCÔNGSUẤTCỦALỰC
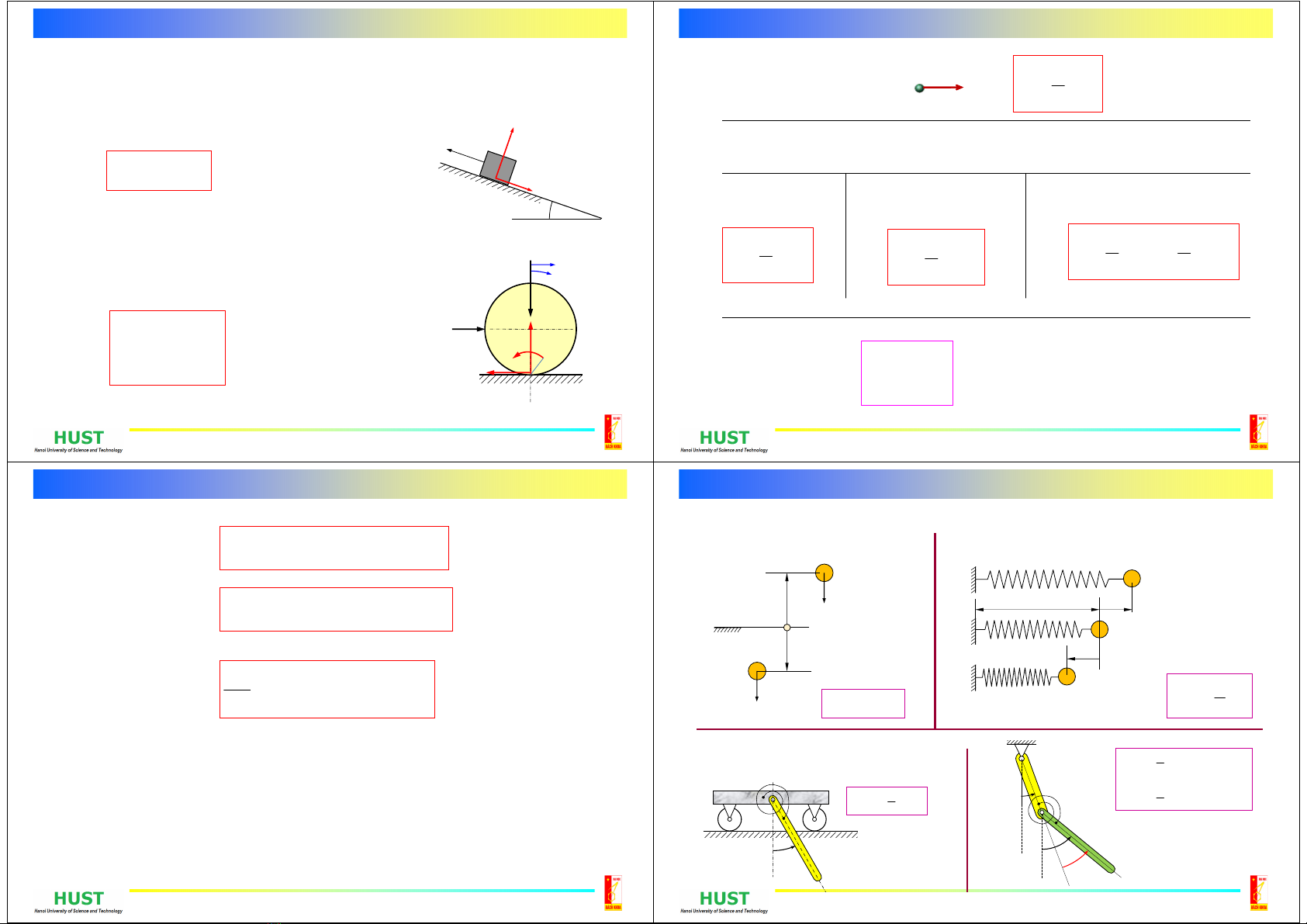
Công của lực ma sát trượt giữa vật với nền
cố định (trường hợp lực ma sát không đổi)
ms
AFs
v
Fms
sN
1.3Côngvàcôngsuấtmộtsốlựcthườnggặp
P
N
Fms
mms
I
F
0
I
v
s
()0
ms
ms
AF
Am
Công của lực ma sát khi vật lăn không trượt trên nền
cố định (trường hợp ngẫu lực ma sát không đổi):
Nguyen Quang Hoang - Department of Applied Mechanics
-6-
2.ĐỘNGNĂNG
CHẤT ĐIỂMmv
2
1
2
Tmv
VẬT RẮN
Hệ n vật rắn
1
n
k
k
TT
Vật quay quanh
trục z cố định
2
1
2
z
TI
Vật tịnh tiến
2
1
2C
Tmv22
11
22
CC
Tmv I
Vật chuyển động phẳng
Nguyen Quang Hoang - Department of Applied Mechanics
-7-
3.ĐỊNHLÝBIẾNTHIÊNĐỘNGNĂNG
a
kk
dT d A F d A
Dạng vi phân
a
kk
dT WF W
dt
Dạng đạo hàm
0
a
kk
TT AF A
Dạng hữu hạn
• Liên kết dây căng không dãn và tại các khớp trơn nhẵn (không
ma sát): nội lực không sinh công.
•Nội lực có thể sinh công hoặc không sinh công tùy thuộc vào từng
trường hợp cụ thể.
Chú ý:
Nguyen Quang Hoang - Department of Applied Mechanics
-8-
4.ĐỊNHLÝBẢOTOÀNCƠNĂNG
yW
=0
=+Wy
=‐Wy
‐y
W
k
l0s
s
=0
=ks2/2
=ks2/2
gmgyP= 2
1
2
eksP=
Thếnăngcủalòxoxoắn
1
2
k
k
ThếnăngcủatrọnglựcThếnăngcủalòxokéonén
2
1
2
kjP=
2
1
2
2
1
21
2()
k
k
q
jj
P=
=-
4.1Thếnăngcủalựccóthế
Nguyen Quang Hoang - Department of Applied Mechanics
-9-
4.ĐỊNHLÝBẢOTOÀNCƠNĂNG
4.2Địnhlýbảotoàncơnăng
Khi cơ hệ chỉ chịu tác dụng của các lực hoạt động có thế, thì tổng động
năng và thế năng của cơ hệ luôn luôn là hằng số
constT
Nguyen Quang Hoang - Department of Applied Mechanics
-10-
Bài 13-2
Bài 13.2
Vật nặng A khối lượng m1 được treo
vào dây mềm không giãn dài l, khối
lượng m. Dây vắt qua ròng rọc B khối
lượng (m3 - đĩa tròn) không đáng kể quay
quanh trục O. Đầu kia của dây buộc vào
trục qua tâm của con lăn C, con lăn C lăn
không trượt trên nền ngang cố định.
Ròng rọc và con lăn là các trục tròn đồng
chất có khối lượng m2, bán kính r .
Tính động năng và thế năng cơ hệ
khi vật A cách nền ngang một đoạn bằng
x và có vận tốc v.
A
C
O
K
B
x
m1
m2
①
③
②
Nguyen Quang Hoang - Department of Applied Mechanics
-11-
Mộtbăng tảivậtliệuđang họat động. Cho
biếtvậtnặng A có khốilượng m1,BvàClàcác
trụđồng chấtcócùng bán kính rvà khốilượng
m2.Băng tải là dây không giãn, đồng chất, khối
lượng m3được phân bốđềutheochiềudài.Bỏ
qua sựtrượtgiữavật A và băng tải, giữacáctrụ
quay và băng tải.
Tính biểu thức động năng của hệ khi trục quay
có vận tốc góc ω.
Bài 13.1
B
AC
Nguyen Quang Hoang - Department of Applied Mechanics
-12-
a) Bỏ qua ma sát ở ổ trục và ma sát lăn của mặt nền. Tìm P sao cho khi người đẩy đi
được s = 2 m thì trục con lăn đạt vận tốc v = 0,8 m/s.
b) Sử dụng dữ kiện của câu a) và tính đến ma sát lăn trên nền với hệ số ma sát lăn
động k = 0,5 cm. Tìm trị số của lực P.
c) Tiếp câu b): sau khi đạt vận tốc cần thiết 0,8 m/s, muốn giữ chuyển động đều của
trục bánh xe ta cần giảm cường độ của lực P đi bao nhiêu?
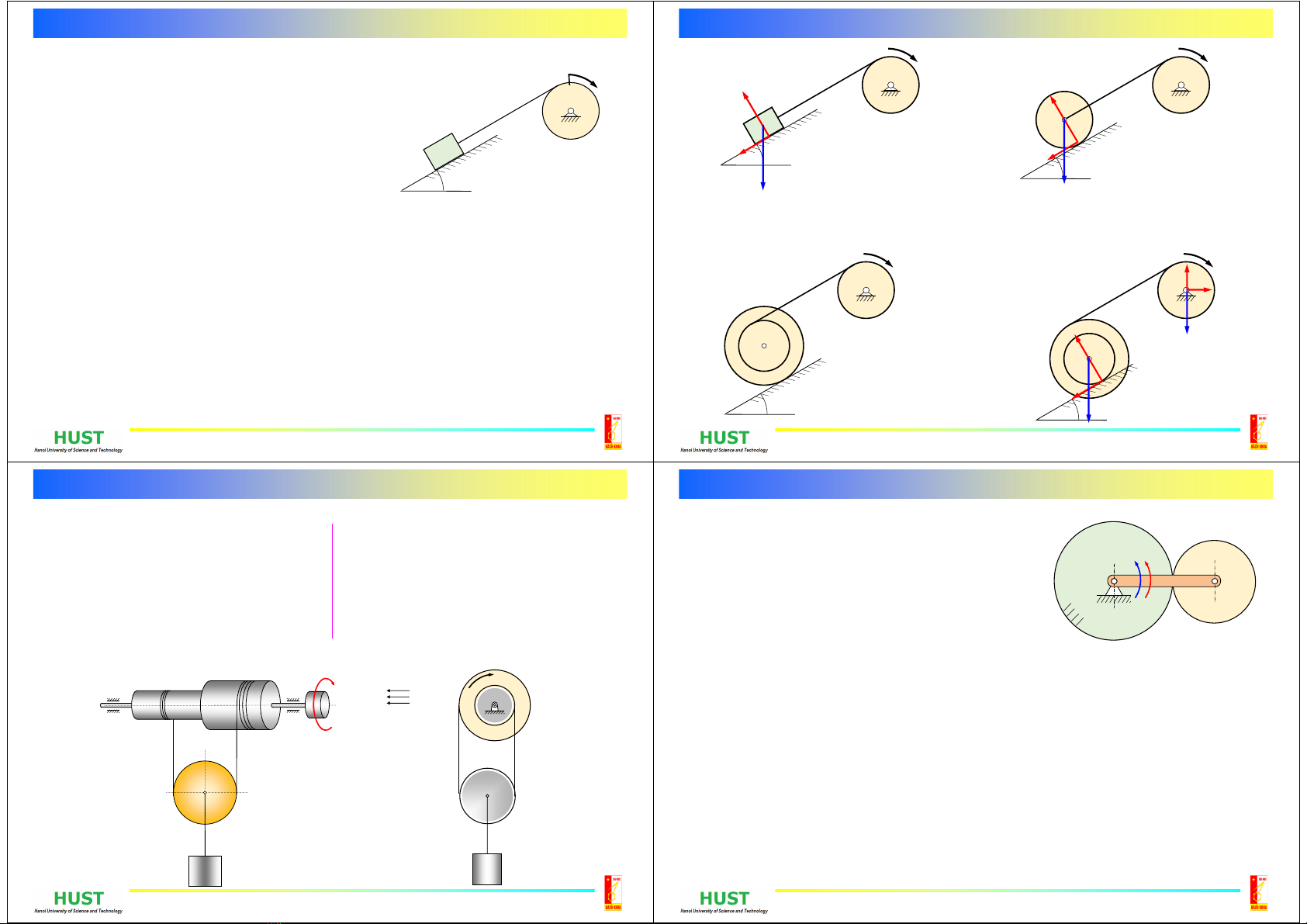
Con lăn dạng trụ tròn đồng chất chuyển động
lăn không trượt từ trạng thái đứng yên trên mặt
phẳng ngang. Thanh đẩy AO có khối lượng
không đáng kể.
m = 392 kg, r = 0,6 m.
AO= l =1,5 m ; h = 1,2 m.
Bài 13.6
O
A
P
h
l
Nguyen Quang Hoang - Department of Applied Mechanics
-13-
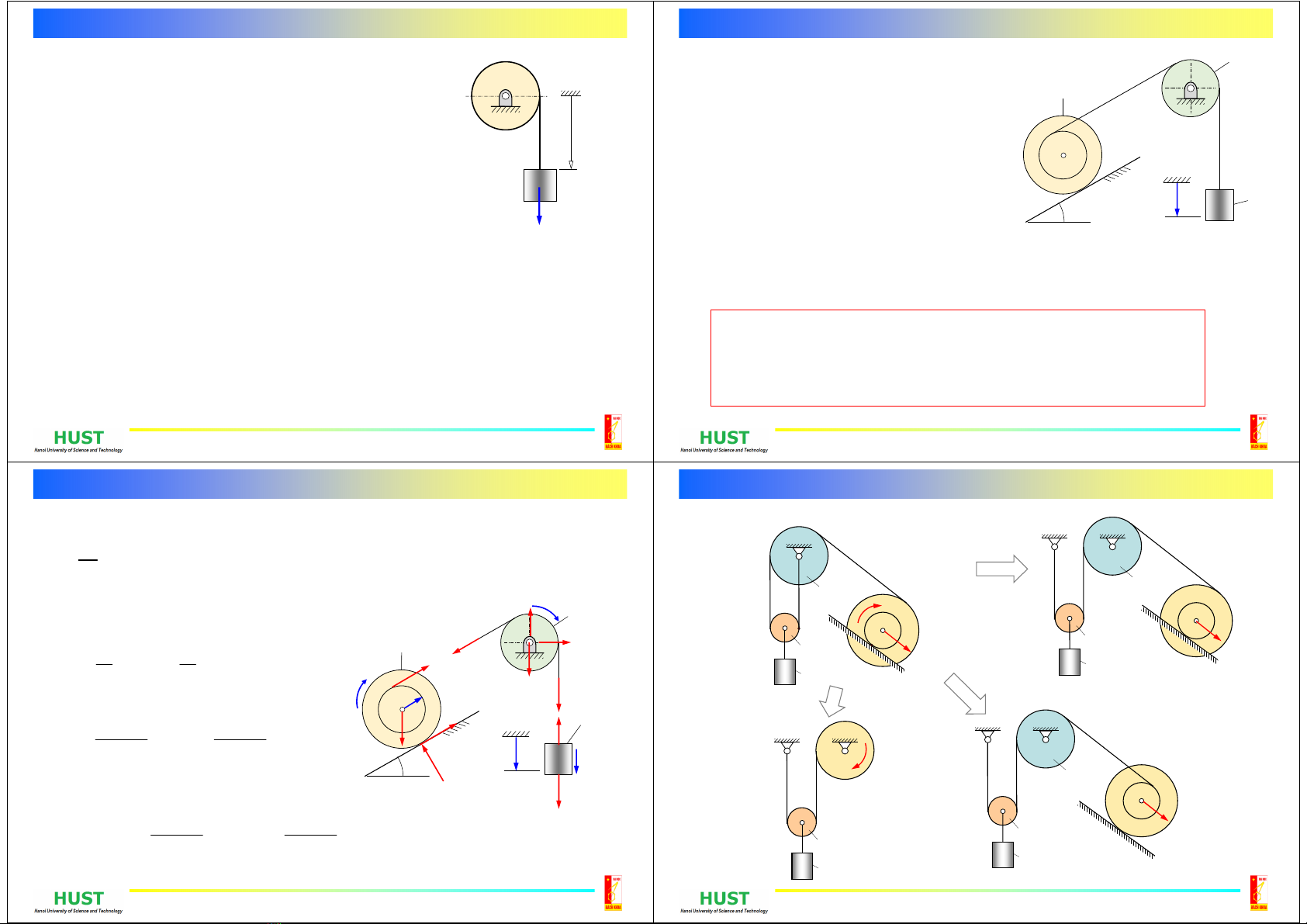
Bài 13.7
Một ngẫu lực có mômen M không đổi tác
dụng lên tang của một trục tời có bán kính
bằng R và có khối lượng là m1.
Quấn vào tang tời một sợi dây mềm nhẹ và
không giãn rồi buộc vào đầu mút tự do của
dây vật nặng A có khối lượng m2 để kéo
nó lên theo mặt phẳng nghiêng, góc
nghiêng là α so với mặt phẳng ngang. Hệ
số ma sát trượt động giữa mặt phẳng và
mặt phẳng nghiêng là f. Tang tời được xem
là một trục tròn đồng chất. Ban đầu hệ
đứng yên.
a) Tìm biểu thức vận tốc góc của tời là hàm theo góc quay của nó, = ().
b) Nếu tại ổ trục O có mô men cản tỷ lệ vận tốc góc Mc = k , tìm hàm (t).
c) Câu hỏi thêm: xác định gia tốc vật A, lực căng dây, phản lực ổ trục O.
OM
A
Nguyen Quang Hoang - Department of Applied Mechanics
-14-
Các bài tương tự
OM
A
OM
A
OM
A
OM
C
2
P
N
ms
F
2
P
N
ms
F
Lực ma sát trượt Fms sinh
công
Lực bám Fms không sinh
công (lăn không trượt)
1
2
Nguyen Quang Hoang - Department of Applied Mechanics
-15-
Bài 13.8
Một tời kéo gồm hai trống:
K1: R1, I1; và K2: R2, I2
Ròng rọc C: m,r (đĩa tròn đồng chất)
Vật D: m3
M=const.
Khi trống K2 quấn dây thì trống
K1 thả dây. Ban đầu hệ đứng yên.
Tìm vận tốc góc của trục tời khi vật
D đã được kéo lên một đoạn bằng h,
tính gia tốc góc của tời.
1
C
2
D
R
r
2
2rRr
M
3
D
C
K1
K2
O1O2
M
Nguyen Quang Hoang - Department of Applied Mechanics
-16-
Bài 13.21
Cơ cấu hành tinh đặt trong mặt phẳng ngang.
Bánh răng 1: r1;
bánh răng 2: m2, r2.
Tay quay OA: m, M
Bỏ qua ảnh hưởng của ma sát.
a) Khi M là hằng số, tìm gia tốc góc của tay quay.
b) Khi , với M0, k là các hằng số.
Tìm biểu thức vận tốc góc của tay quay là hàm theo thời gian.
0
M
Mk
OA
M
1
2
Nguyen Quang Hoang - Department of Applied Mechanics
-17-
Bài 13.9
Một vật nặng P được treo vào đầu một sợi dây mềm không
giãn, chiều dài L và trọng lượng trên một đơn vị chiều dài
của dây là p. Dây này được quấn vào tang của một trục tời có
bán kính bằng r và có mômen quán tính khối đối với trục
quay là IO. Vật nặng rơi xuống làm quay trục tời.
Lúc ban đầu đoạn dây treo buông dài xuống một đoạn x0 và
hệ đứng yên. Bỏ qua ma sát của các ổ trục quay và chiều dài
của dây cũng như sự thay đổi thế năng của phần dây quấn.
Xác định vận tốc rơi của vật nặng là hàm theo độ dài x của
đoạn dây treo.
B
A
P
O
x0+x
Nguyen Quang Hoang - Department of Applied Mechanics
-18-
Bài 13.19
Cho vật 1: m1; ròng rọc 2: m2, r2;
Con lăn 3: m3, R3, r3, ρ, lăn không trượt.
Ban đầu hệ đứng yên, h = 0.
Tìm v1(h)? C
1
2
3
O
h
Câu hỏi phụ: tính lực căng các nhánh dây. Lực tại điểm tiếp xúc giữa con
lăn và mặt nghiêng.
HD:
- Tính gia tốc vật 1 suy ra gia tốc các vật.
-Cắt dây – tách vật, Viết phương trình lực – gia tốc cho các vật.
Nguyen Quang Hoang - Department of Applied Mechanics
-19-
1
v
3
1
P
2
C
1
2
3
O
h
Td2
Td1
N
F
3
P
C
v
11 1 1 1
W/
tg td td tg
dTMvv Fv a v FM
dt
4. Tính gia tốc vật 1 và các gia tốc …..
33
33 1 1
33 33
CC
RR
vR vv v
rR rR
11
22
22
vv
rr
11
33
33 33
vv
rR rR
Tính gia tốc góc vật 2, 3, gia tốc tâm C
Nguyen Quang Hoang - Department of Applied Mechanics
-20-
Các bài tương tự
2
1
3
4
C
A
K
B
D
E
F
G
v0
0
1
2
3
A
B
D
E
0
2
1
3
4
C
A
K
B
D
E
F
G
v0
0
2
1
3
4
C
A
K
B
D
E
F
G
v0
0








![Bài giảng Đại cương về kỹ thuật Trường Đại học Kỹ thuật Công nghiệp [Tài liệu đầy đủ]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250107/nienniennhuy44/135x160/3791736217643.jpg)


![Bài tập tối ưu trong gia công cắt gọt [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251129/dinhd8055/135x160/26351764558606.jpg)














