Nguyen Quang Hoang - Department of Applied Mechanics
-1-
Xung lực, động lượng
Định lý biến thiên động lượng
Định lý biến thiên mô men động lượng
Tóm tắt lý thuyết
Quan hệ xung lực và động lượng
Principle of Impulse and Momentum
Nguyen Quang Hoang - Department of Applied Mechanics
-2-
()dS F t dt

1. XUNG LỰC (xung lượng, xung lượng của lực)
Đơn vị của xung lực là Newton-giây [N.s]
pmv
1
n
kk
k
pmv
[kg.m/s]
k
x
k
y
k
z
x
y
z
mk
O
m1
kk
mv
Động lượng của hệ n chất điểm
2. ĐỘNG LƯỢNG
1. Xung lực - động lượng
2
1
()
t
t
SFtdt

Nguyen Quang Hoang - Department of Applied Mechanics
-3-
C
pvdmmv

x
y
z
O
C
x
y
z
vdm
r
C
r
u
Động lượng của vật rắn
Động lượng củacơhệ
(các vậtrắnvàcácchấtđiểm)
11
()
p
n
kk iCi k C
ki
pmv mv mv




2. Động lượng
Nguyen Quang Hoang - Department of Applied Mechanics
-4-
21
()
() ()
d mv Fdt dS
pt pt S




Đối với chất điểm
21
() ()
ee
kCk
kk
e
k
k
dp Fma F
dt
pt pt S





Đối với cơ hệ
0
e
kC
k
Fmvconst

0
e
kx C
k
Fmxconst

Các trường hợpbảotoàn
3. Định lý biến thiên động lượng
Nguyen Quang Hoang - Department of Applied Mechanics
-5-
BÀI TẬP
Nguyen Quang Hoang - Department of Applied Mechanics
-6-
12.6Xeđẩycókhốilượngm2=25kgđangđứngyên.Kiện
hàngkhốilượngm1=10kgtrượttheomặtphẳngnghiêng
xuốngxevớivậntốcv1=3m/slàmchoxechuyểnđộng
trênnềntrơnnhẵn.Hãyxácđịnh:
a) Vậntốccủaxe
b) Xunglựcdokiệnhàngtácdụnglênxe.
v1
30
Bài 12-6.
Nguyen Quang Hoang - Department of Applied Mechanics
-7-
12.11.Cơhệgồm:vậtA:m1,lăngtrụ:m2,
.Lăngtrụđặttrên
mặtngangnhẵnnhưhìnhvẽ.Khit=0:vậtAnằmyêntương
đốitrênmặtlăngtrụ,lăngtrụtrượtngangsangphảivớivận
tốcv0.SauđóchovậtAtrượtxuốngtheomặtphẳngnghiêng
củalăngtrụvớivậntốctươngđốiu=at.Tìmvậntốccủalăng
trụ.
v0
u
A
m1
m2
x
y
Bài 12-11.
Nguyen Quang Hoang - Department of Applied Mechanics
-8-
12.15.TrênmộtxàlanAkhốilượngMđangđứngyêncómộtô‐tôkhối
lượngmchuyểnđộngtheoquyluậts(t)=s0+b(αt+e‐αt‐1),bỏqualựccản
củanướclênxàlan.
a) XácđịnhvậntốccủaxàlanvA(t).
b) Nếuxàlanđượcgiữcốđịnhbằngmộtdâyneonằmngang,xácđịnhlực
căngdâyneo.
s(t)
AM
m
Bài 12-15.
x
y
P
p
N
0
() ( 1)
t
st s b t e a
a-
=+ + -
Nguyen Quang Hoang - Department of Applied Mechanics
-9-
b) Nếuxàlanđượcgiữcốđịnh bằng
mộtdâyneonằm ngang, xác định lực
căng dây neo.
Bài 12-15.
s(t)
A
x(t)
Mg
mg
N
F
Nguyen Quang Hoang - Department of Applied Mechanics
-10-
12‐9.MộttàuthủycókhốilượngM=200tấn,chuyểnđộngvớitốcđộtrung
bình10m/stheođườngthẳngngangtrênmặtnướcyêntĩnh.Pistoncủamáy
hơinướccókhốilượngm=100kgchuyểnđộngtheođườngthẳngsongsong
vớitrụcdọccủatàu.Pistonthựchiện240hànhtrìnhtrong1phútvớiđộdài
hànhtrìnhlà1m.Coichuyểnđộngcủapistonlàdaođộngđiềuhòa.Xácđịnh
biểuthứcvậntốccủatàunếusứcđẩycủachânvịtluôncânbằngvớilựccản
củanước.
Bài 12-9.
s(t)
A
Fd
Fc
x(t)
0
0
() sin ,
, 0,5 m
st s A t
sconstA
w=+
==
v
Nguyen Quang Hoang - Department of Applied Mechanics
-11-
Momen động lượng
Mômen động lượng của
chất điểm đối với tâm O
()
OO
lmmv
O
lrmv
Mômen động lượng của
chấtđiểmđốivớitrụcz
qua O
()
Oz Oz
lmmv
4. Định lý biến thiên mô men động lượng
mv
z
x
y
r
A
O
xyz
eee{, , }

O
l
Oz
l
Nguyen Quang Hoang - Department of Applied Mechanics
-12-
Momen động lượng
Mômen động lượng của VR quay
quanh trục z cố định
zz
lIw=
Mômen động lượng của tấm
phẳng chuyển động song phẳng
CC
lIw=
4. Định lý biến thiên mô men động lượng
z
dm
hv
w
C
u
udmw´
w
Nguyen Quang Hoang - Department of Applied Mechanics
-13-
Định lý 1 (đ/v chất điểm)
OOk
k
dlmF
dt (),=
å
Oz Oz k
k
dlmF
dt ()
Định lý 2.(đ/v cơhệ)
e
OOk
k
dlmF
dt (),=
å
e
Oz Oz k
k
dlmF
dt ()
() 0 ,
e
Ok O
k
If m F l const= =
å
Các trường hợpbảotoàn
4. Định lý biến thiên mô men động lượng
O cố định
O cố định
() 0 ,
e
zk z
k
If m F l const==
å
Nguyen Quang Hoang - Department of Applied Mechanics
-14-
A child (mass m) runs along the rim of a
circular platform (mass M,radiusr) starting
from point A. The platform is initially at
rest; its support is frictionless. Determine the
angle of rotation of the platform when the
child arrives again at point A.
Nguyen Quang Hoang - Department of Applied Mechanics
-15-
Ru
w
A
B
M
z
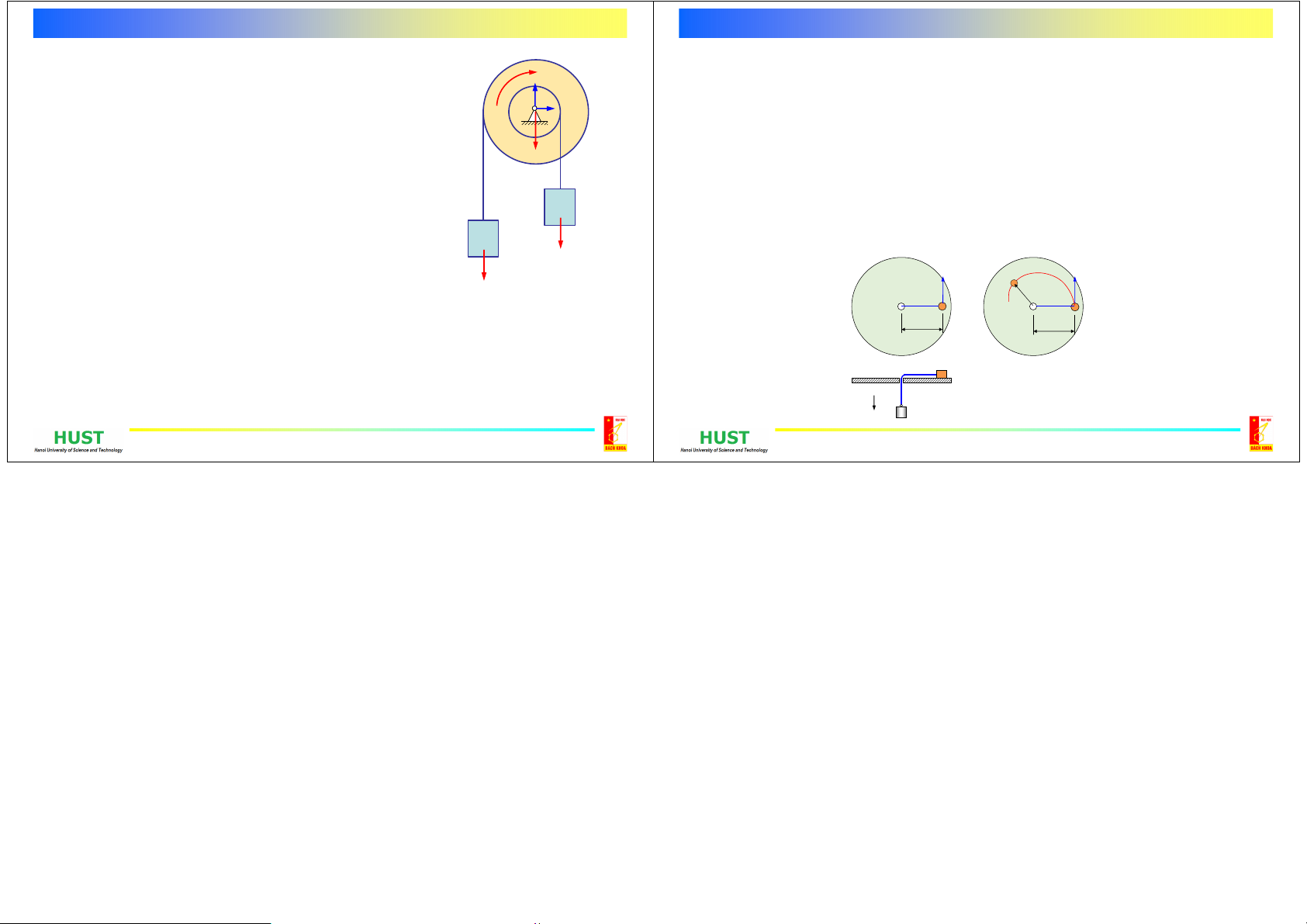
12.16. Đĩa đồng chất: R, m. Xe con M (chất điểm):
m0. Tại t=0: đĩa quay với
0, chất điểm đứng yên
trên vành đĩa. Tìm vận tốc góc
của đĩa khi chất
điểm chuyển động theo vành đĩa với vr = u.
P0
P
e
v
Bài 12-16.
Nguyen Quang Hoang - Department of Applied Mechanics
-16-
12‐17.Chođĩatrònđồngchất:m1,r,ω
0.Vàothờiđiểm
nàođó,xeconM(chấtđiểm):m2,bắtđầuchuyểnđộngtừ
tâmđĩarangoàivớivậntốcukhôngđổi.Bỏquamasáttạiổ
trục.
Tìmω(t)kểtừlúcchấtđiểmMchuyểnđộng.u
B
X
B
Y
A
X
A
Y
A
Z
1
P2
P
e
v
Bài 12-17.
Nguyen Quang Hoang - Department of Applied Mechanics
-17-
12‐18.HaivậtnặngAvàBcókhốilượngtươngứngm1vàm2
đượctreovàohaiđầucủadâykhôngtrọnglượng.Dâyđược
quấnvàotangtờiChaitầngcóbánkínhrvàR.ĐểnângvậtB
lênngườitatácdụngmộtngẫulựccómomenMlêntờinhư
hìnhvẽ.Biếttờicókhốilượngm,bánkínhquántínhvớitrục
quayρ.TìmgiatốcgóccủatờiC.
B
A
O
C
M
m2g
m1g
mg
XO
YO
Bài 12-18.
Nguyen Quang Hoang - Department of Applied Mechanics
-18-
Bài tập tổng hợp
Hai vậtnhỏAvàBcókhốilượng tương ứng m1và m2đượcgắnvàomộtsợi
dây mềm không dãn luồn qua mộtlỗtạiOtrênmộtchiếcbànnhẵn. Khi A
cách lỗr0,nóthựchiện chuyểnđộng tròn vớivậntốcv
0vuông góc OA trên
mặtbànnằm ngang không ma sát. Tạithờiđiểmvật A nó cách lỗOđoạnr,
hãy xác định:
a) Vậntốccủavật(điểm) A; VậntốcvậtB.
b) Lựccăng dây phụthuộc vào khoảng cách r;
OAA
O
O
B
g
A
0
r
0
v
0
r
r
0
v