zunia.vn

Tuyển sinh 2024 dành cho Gen-Z

zunia.vn

» Kinh Tế - Quản Lý

» Kinh tế học

Bài giảng Kinh tế lượng 1: Chương 2 - Trường ĐH Kinh tế Quốc Dân (Năm 2022)

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:31

Báo xấu

10
lượt xem 3
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng Kinh tế lượng 1: Chương 2 được biên soạn gồm các nội dung chính sau: Sự cần thiết của hồi quy bội; Phương pháp ước lượng OLS; Sự phù hợp của hàm hồi quy; Một số dạng mô hình hồi quy. Mời các bạn cùng tham khảo!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Kinh tế lượng 1: Chương 2 - Trường ĐH Kinh tế Quốc Dân (Năm 2022)

Chương 2. MÔ HÌNH HỒI QUY BỘI ▪ 2.1. Sự cần thiết của hồi quy bội ▪ 2.2. Phương pháp ước lượng OLS ▪ 2.3. Sự phù hợp của hàm hồi quy ▪ 2.4. Một số dạng mô hình hồi quy KINH TẾ LƯỢNG 1 – Bộ môn Toán kinh tế – NEU – www.mfe.edu.vn 50
Hồi quy đơn và Hồi quy bội ▪ Đặt k là số hệ số có trong mô hình ▪ Mô hình có hệ số chặn thì số biến bằng 𝑘, số biến độc lập không kể hằng số bằng (𝑘 − 1) ▪ Với 𝑘 = 2 là hồi quy đơn (single-regression) ▪ Với 𝑘 ≥ 2: hai biến độc lập trở lên, gọi là hồi quy bội (multi-regression) hay hồi quy đa biến (multivariate regression) KINH TẾ LƯỢNG 1 – Bộ môn Toán kinh tế – NEU – www.mfe.edu.vn 51
Chương 2. Mô hình hồi quy bội 2.1. SỰ CẦN THIẾT CỦA HỒI QUY BỘI ▪ Hồi quy đơn: 𝑌 = 𝛽1 + 𝛽2 𝑋 + 𝑢 ▪ Nếu u có tương quan với X: 𝐶𝑜𝑣(𝑢, 𝑋) ≠ 0 thì X gọi là biến độc lập nội sinh. → giả thiết 2 bị vi phạm → các ước lượng là chệch. ▪ Yếu tố có tương quan với 𝑋 trong 𝑢, giả sử là 𝑍 ▪ 𝑍 là biến độc lập mới, mô hình có dạng 𝑌 = 𝛽1 + 𝛽2 𝑋 + 𝛽3 𝑍 + 𝑢 KINH TẾ LƯỢNG 1 – Bộ môn Toán kinh tế – NEU – www.mfe.edu.vn 52
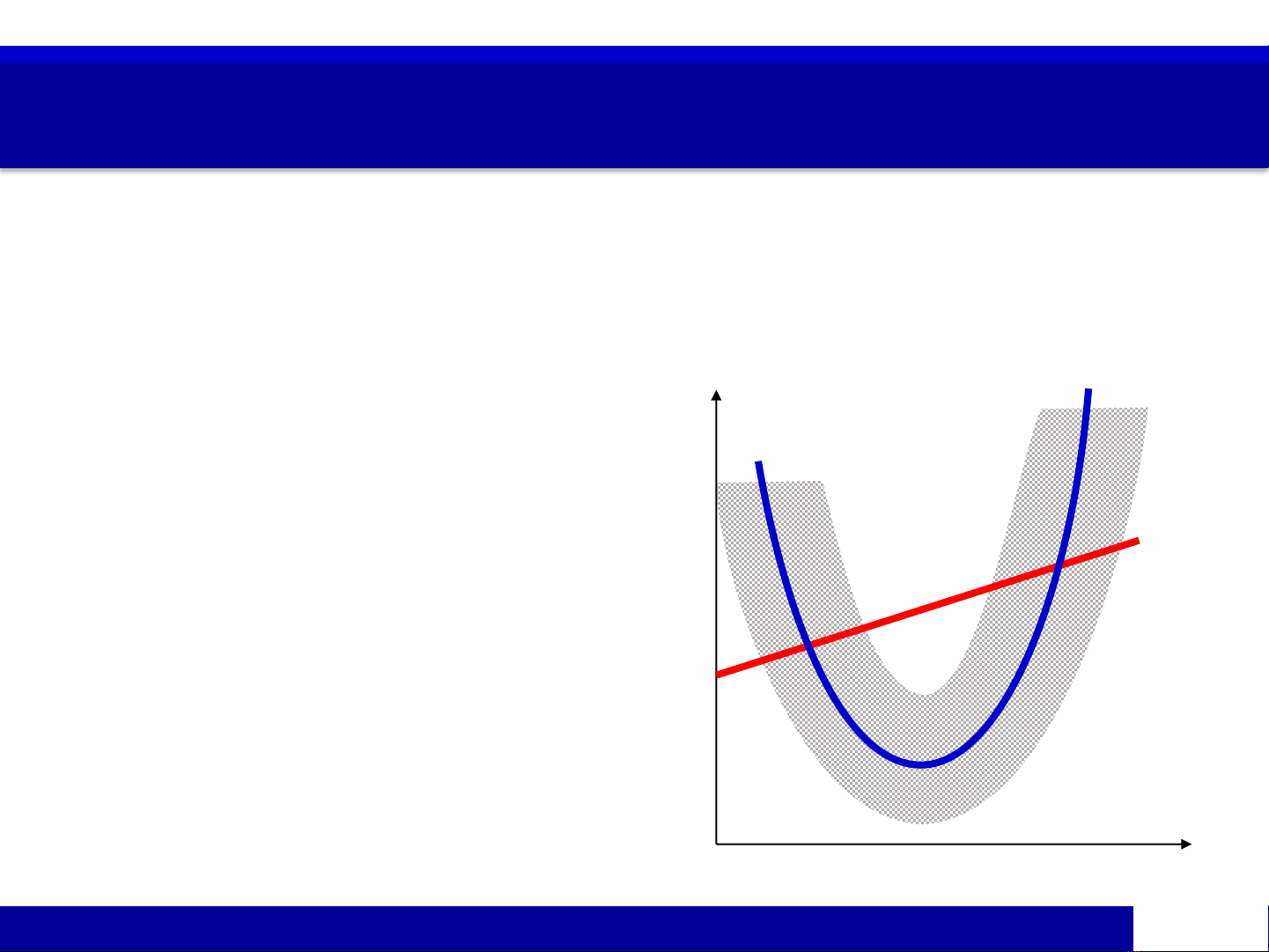
Chương 2. Mô hình hồi quy bội 2.1. Sự cần thiết của hồi quy bội Vấn đề dạng hàm hồi quy ▪ Hồi quy đơn hạn chế về dạng hàm ▪ Hồi quy bội có dạng hàm phù hợp hơn, dự báo tốt 𝛽1 + 𝛽2 𝑋 + 𝛽3 𝑋 2 hơn ▪ Phong phú hơn trong phân tích kinh tế 𝛽1 + 𝛽2 𝑋 KINH TẾ LƯỢNG 1 – Bộ môn Toán kinh tế – NEU – www.mfe.edu.vn 53
Chương 2. Mô hình hồi quy bội 2.1. Sự cần thiết của hồi quy bội Mô hình hồi quy ba biến ▪ Biến Y phụ thuộc vào 2 biến độc lập 𝑋2 , 𝑋3 𝑌 = 𝛽1 + 𝛽2 𝑋2 + 𝛽3 𝑋3 + 𝑢 ▪ PRF: 𝐸 𝑌 𝑋2 , 𝑋3 ) = 𝛽1 + 𝛽2 𝑋2 + 𝛽3 𝑋3 ▪ SRF: 𝑌෠𝑖 = 𝛽መ1 + 𝛽መ2 𝑋2𝑖 + 𝛽መ3 𝑋3𝑖 ▪ Nếu X2, X3 có quan hệ cộng tuyến: 𝑋3 = 𝛼1 + 𝛼2 𝑋2 thì 𝑌 = 𝛽1 + 𝛼1 𝛽3 + 𝛽2 + 𝛼2 𝛽3 𝑋2 + 𝑢 ▪ Mô hình ba biến chỉ đúng khi các biến độc lập không có quan hệ cộng tuyến KINH TẾ LƯỢNG 1 – Bộ môn Toán kinh tế – NEU – www.mfe.edu.vn 54
Chương 2. Mô hình hồi quy bội 2.1. Sự cần thiết của hồi quy bội Mô hình hồi quy k biến ▪ Mô hình có (𝑘 − 1) biến độc lập, 𝑘 hệ số: 𝑌 = 𝛽1 + 𝛽2 𝑋2 + 𝛽3 𝑋3 + ⋯ + 𝛽𝑘 𝑋𝑘 + 𝑢 𝐸(𝑌|𝑋2 , … , 𝑋𝑘 ) = 𝛽1 + 𝛽2 𝑋2 + 𝛽3 𝑋3 + ⋯ + 𝛽𝑘 𝑋𝑘 ▪ Ý nghĩa hệ số: • Hệ số chặn: 𝛽1 = 𝐸 𝑌 𝑋2 = ⋯ = 𝑋𝑘 = 0 • Hệ số góc: 𝛽𝑗 (𝑗 = 2, 𝑘): tác động riêng của Xj 𝜕𝐸 𝑌 𝛽𝑗 = 𝜕𝑋𝑗 ▪ Nếu 𝛽2 = ⋯ = 𝛽𝑘 = 0: hàm hồi quy không phù hợp KINH TẾ LƯỢNG 1 – Bộ môn Toán kinh tế – NEU – www.mfe.edu.vn 55
Chương 2. Mô hình hồi quy bội 2.1. Sự cần thiết của hồi quy bội Mô hình hồi quy k biến ▪ Mô hình trong mẫu • 𝑌෠𝑖 = 𝛽መ1 + 𝛽መ2 𝑋2𝑖 + 𝛽መ3 𝑋3𝑖 + ⋯ + 𝛽መ𝑘 𝑋𝑘𝑖 • 𝑌𝑖 = 𝛽መ1 + 𝛽መ2 𝑋2𝑖 + 𝛽መ3 𝑋3𝑖 + ⋯ + 𝛽መ𝑘 𝑋𝑘𝑖 + 𝑒𝑖 ▪ Mô hình k biến chỉ đúng khi các biến độc lập không được quan hệ cộng tuyến với nhau: • Không tồn tại các hằng số 𝜆1 , 𝜆2 , … , 𝜆𝑘 không đồng thời bằng 0 sao cho: 𝜆1 + 𝜆2 𝑋2 + ⋯ + 𝜆𝑘 𝑋𝑘 = 0 ▪ 𝛽መ𝑗 là ước lượng điểm cho 𝛽𝑗 (𝑗 − 1, 𝑘) KINH TẾ LƯỢNG 1 – Bộ môn Toán kinh tế – NEU – www.mfe.edu.vn 56
Chương 2. Mô hình hồi quy bội 2.2. PHƯƠNG PHÁP ƯỚC LƯỢNG OLS ▪ Tìm 𝛽መ𝑗 sao cho ( ) n n 2 RSS =  e =  Yi − ˆ1 − ˆ2 X 2i − ... − ˆk X ki 2 i → min i =1 i =1 ▪ Giải hệ k phương trình bậc nhất k ẩn ▪ Cách giải qua ma trận ▪ Để giải được nghiệm: các biến độc lập không được có quan hệ cộng tuyến hoàn toàn với nhau KINH TẾ LƯỢNG 1 – Bộ môn Toán kinh tế – NEU – www.mfe.edu.vn 57
Chương 2. Mô hình hồi quy bội 2.2. Phương pháp ước lượng OLS Các giả thiết OLS ▪ Giả thiết 1: Mẫu là ngẫu nhiên, độc lập (𝑋2𝑖 , … , 𝑋𝑘𝑖 , 𝑌𝑖 ), 𝑖 = 1, 𝑛 là độc lập ▪ Giả thiết 2: Kì vọng sai số ngẫu nhiên bằng 0 𝐸 𝑢 𝑋2 , … , 𝑋𝑘 ) = 0 hay 𝐸 𝑢𝑖 𝑋2𝑖 , … , 𝑋𝑘𝑖 ) = 0 ▪ Giả thiết 3: Phương sai sai số ngẫu nhiên không đổi 𝑉𝑎𝑟 𝑢 𝑋2 , … , 𝑋𝑘 ) = 𝜎 2 ▪ Giả thiết 4: Các biến độc lập không có quan hệ cộng tuyến hoàn hảo KINH TẾ LƯỢNG 1 – Bộ môn Toán kinh tế – NEU – www.mfe.edu.vn 58
Chương 2. Mô hình hồi quy bội 2.2. Phương pháp ước lượng OLS Định lý Gauss – Markov ▪ Định lý: Khi các giả thiết 1 đến 4 được thỏa mãn thì các ước lượng OLS là các ước lượng tuyến tính, không chệch, tốt nhất (trong lớp các ước lượng tuyến tính không chệch) ▪ 𝛽መ𝑗𝑂𝐿𝑆 là BLUE: Best Linear Unbiased Estimator ▪ 𝛽መ𝑗𝑂𝐿𝑆 là ước lượng tuyến tính, không chệch, tốt nhất của 𝛽𝑗 (𝑗 = 1, 𝑘) KINH TẾ LƯỢNG 1 – Bộ môn Toán kinh tế – NEU – www.mfe.edu.vn 59
Chương 2. Mô hình hồi quy bội 2.2. Phương pháp ước lượng OLS Tính vững của ước lượng ▪ Ước lượng vững (consistent estimator): khi kích thước mẫu rất lớn thì ước lượng hệ số trong mẫu tiệm cận hệ số trong tổng thể ▪ Nếu các giả thiết OLS được thỏa mãn thì ước lượng OLS là ước lượng vững ▪ Nếu mẫu lớn, có thể thay giả thiết 2 bởi những giả thiết bớt chặt hơn mà vẫn đảm bảo tính vững ▪ Khi không thể có ước lượng không chệch, ước lượng vững cũng có thể dùng được. KINH TẾ LƯỢNG 1 – Bộ môn Toán kinh tế – NEU – www.mfe.edu.vn 60
Chương 2. Mô hình hồi quy bội 2.2. Phương pháp ước lượng OLS Độ chính xác của ước lượng OLS ▪ Kỳ vọng của ước lượng: 𝐸 𝛽መ𝑗 = 𝛽𝑗 ▪ Phương sai: 𝜎2 𝑉𝑎𝑟 𝛽መ𝑗 = 2 1− 𝑅𝑗2 σ 𝑋𝑗𝑖 − 𝑋ത𝑗 ▪ Với 𝑅𝑗2 là hệ số xác định khi hồi quy 𝑋𝑗 theo các biến độc lập còn lại, có hệ số chặn ▪ 𝑋𝑗 tương quan với các biến còn lại càng nhiều → 𝑉𝑎𝑟(𝛽መ𝑗 ) càng lớn KINH TẾ LƯỢNG 1 – Bộ môn Toán kinh tế – NEU – www.mfe.edu.vn 61
Chương 2. Mô hình hồi quy bội 2.2. Phương pháp ước lượng OLS Độ chính xác của ước lượng OLS ▪ Phương sai sai số ngẫu nhiên được ước lượng bởi 2 𝑅𝑆𝑆 𝜎ො = 𝑛−𝑘 ▪ Thay 𝜎ො 2 vào công thức 𝑉𝑎𝑟(𝛽መ𝑗 ), được 𝑉𝑎𝑟 ෢ 𝛽መ𝑗 ▪ Sai số chuẩn của ước lượng: 𝑆𝑒 𝛽መ𝑗 = ෢ 𝛽መ𝑗 𝑉𝑎𝑟 ▪ Tính được các hiệp phương sai của các cặp ước lượng hệ số: 𝐶𝑜𝑣 𝛽መ𝑗 , 𝛽መ𝑠 , 𝑗 ≠ 𝑠 KINH TẾ LƯỢNG 1 – Bộ môn Toán kinh tế – NEU – www.mfe.edu.vn 62
Chương 2. Mô hình hồi quy bội 2.2. Phương pháp ước lượng OLS Sự tác động đến ước lượng hệ số ▪ Xét mô hình: 𝑌 = 𝛽1 + 𝛽2 𝑋2 + 𝑢 ; 𝑌෠𝑖 = 𝛽መ1 + 𝛽መ2 𝑋2𝑖 ▪ Khi thêm biến Z: 𝑌 = 𝛽1∗ + 𝛽2∗ 𝑋2 + 𝛽3 𝑍 + 𝑢 𝑌෠𝑖 = 𝛽መ1∗ + 𝛽መ2∗ 𝑋𝑖 + 𝛽መ3 𝑍𝑖 ▪ Ước lượng hệ số biến X không đổi: 𝛽መ2 = 𝛽መ2∗ nếu: • Ước lượng hệ số biến Z bằng 0: 𝛽መ3 = 0 • Hoặc hệ số tương quan mẫu X và Z bằng 0: rX,Z = 0 ▪ Tổng quát: Nếu tất cả các biến thêm vào đều không tương quan với biến X thì ước lượng hệ số của X sẽ không đổi KINH TẾ LƯỢNG 1 – Bộ môn Toán kinh tế – NEU – www.mfe.edu.vn 63
Chương 2. Mô hình hồi quy bội 2.3. SỰ PHÙ HỢP CỦA HÀM HỒI QUY MẪU ▪ Hệ số xác định (bội) 𝟐 𝐸𝑆𝑆 𝑅𝑆𝑆 𝑹 = =1− 𝑇𝑆𝑆 𝑇𝑆𝑆 ▪ 𝑅2 ∈ [0, 1] ▪ Cho biết tỉ lệ (%) sự biến động trong mẫu của biến phụ thuộc được giải thích bởi mô hình (bởi sự biến động của tất cả các biến độc lập). ▪ 𝑅2 = 0: tất cả các biến độc lập đều không giải thích 2 ▪ 𝑅2 = 𝑟𝑌,𝑌 ෠ KINH TẾ LƯỢNG 1 – Bộ môn Toán kinh tế – NEU – www.mfe.edu.vn 64
Chương 2. Mô hình hồi quy bội 2.3. Sự phù hợp của hàm hồi quy mẫu Hệ số xác định (bội) điều chỉnh ▪ Thêm biến độc lập → 𝑅2 tăng lên ▪ Mô hình có 𝑅2 lớn hơn chưa chắc tốt hơn ▪ Hệ số xác định điều chỉnh (Adjuted R-squared) 𝑅𝑆𝑆/(𝑛 − 𝑘) 𝑛−1 =1−𝑅ത 2 =1− 1−𝑅 2 𝑇𝑆𝑆/(𝑛 − 1) 𝑛−𝑘 ▪ Dấu hiệu nên thêm biến vào mô hình: 𝑅ത 2 tăng KINH TẾ LƯỢNG 1 – Bộ môn Toán kinh tế – NEU – www.mfe.edu.vn 65
Chương 2. Mô hình hồi quy bội 2.4. MỘT SỐ DẠNG MÔ HÌNH HỒI QUY ▪ Xét các mô hình kinh tế đưa được về hồi quy tuyến tính theo hệ số ▪ Hàm tuyến tính (linear-linear) ▪ Hàm logarit (log-log) ▪ Hàm nửa logarit (lin-log và log-lin) ▪ Hàm đa thức theo biến độc lập KINH TẾ LƯỢNG 1 – Bộ môn Toán kinh tế – NEU – www.mfe.edu.vn 66
Chương 2. Mô hình hồi quy bội 2.4. Một số dạng mô hình hồi quy Mô hình dạng tuyến tính theo biến ▪ Còn gọi là linear-linear ▪ Ví dụ: Hàm cầu tiêu dùng hàng hóa: 𝐷𝐴 = 𝛽1 + 𝛽2 𝑌 𝑑 + 𝛽3 𝑃𝐴 + 𝛽4 𝑃𝑆 + 𝛽5 𝑃𝐶 + 𝑢 • Với DA là lượng cầu hàng hóa A, 𝑌 𝑑 là thu nhập khả dụng, 𝑃𝐴 là giá hàng hóa A, 𝑃𝑆 là giá hàng hóa thay thế, 𝑃𝐶 là giá hàng hóa bổ sung • Theo hệ số 𝛽2 thì phân loại hàng hóa A thế nào? • Dấu các hệ số góc như thế nào thì phù hợp? KINH TẾ LƯỢNG 1 – Bộ môn Toán kinh tế – NEU – www.mfe.edu.vn 67
Chương 2. Mô hình hồi quy bội 2.4. Một số dạng mô hình hồi quy Mô hình dạng log-log ▪ Hàm sản xuất Cobb-Douglas: 𝑄 = 𝐴. 𝐾𝛽2 𝐿𝛽3 ▪ Thêm sai số: 𝑄 = 𝐴. 𝐾𝛽2 𝐿𝛽3 𝑒 𝑢 ▪ Logarit: ln 𝑄 = ln 𝐴 + 𝛽2 ln 𝐾 + 𝛽3 ln 𝐿 + 𝑢 ▪ Tổng quát: ln 𝑌 = 𝛽1 + 𝛽2 ln 𝑋2 + ⋯ + 𝛽𝑘 ln 𝑋𝑘 + 𝑢 𝑑𝑌 𝑑𝑋2 • Vi phân hai vế: = 𝛽2 𝑌 𝑋2 • 𝛽2 = 𝜀𝑌/𝑋2 là độ co giãn của Y theo 𝑋2 • Khi 𝑋2 tăng 1%, trung bình Y tăng 𝛽2 % KINH TẾ LƯỢNG 1 – Bộ môn Toán kinh tế – NEU – www.mfe.edu.vn 68
Chương 2. Mô hình hồi quy bội 2.4. Một số dạng mô hình hồi quy Mô hình dạng log-log ▪ Ví dụ: Phân tích kết quả ước lượng hàm sản xuất như sau: ෣ = 0,23 + 0,62 ln 𝐾 + 0,57ln(𝐿) ln(𝑄) Với Q là sản lượng, K là vốn, L là lao động ▪ Ví dụ: Khi nào hàng hóa là thấp cấp, thông thường, thiết yếu, xa xỉ nếu hàm cầu theo thu nhập khả dụng có dạng: ln 𝐷 = 𝛽1 + 𝛽2 ln(𝑌 𝑑 ) + 𝑢 KINH TẾ LƯỢNG 1 – Bộ môn Toán kinh tế – NEU – www.mfe.edu.vn 69

CÓ THỂ BẠN MUỐN DOWNLOAD

CEO.17: Bộ Tài Liệu Tiêu Chuẩn ISO 9000 Trong Doanh Nghiệp Sản Xuất

36 tài liệu

2073 lượt tải

THÔNG TIN

TRỢ GIÚP

HỖ TRỢ KHÁCH HÀNG

Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.