CÂY
CHƯƠNG6
TônQuangToại
KhoaCNTT,ĐạihọcNgoạingữ‐ TinhọcTP.HCM
KháiniệmCây
CáctínhchấtcơbảncủaCây
Câykhungcủađồthị
Câykhungnhỏnhất
Nộidung
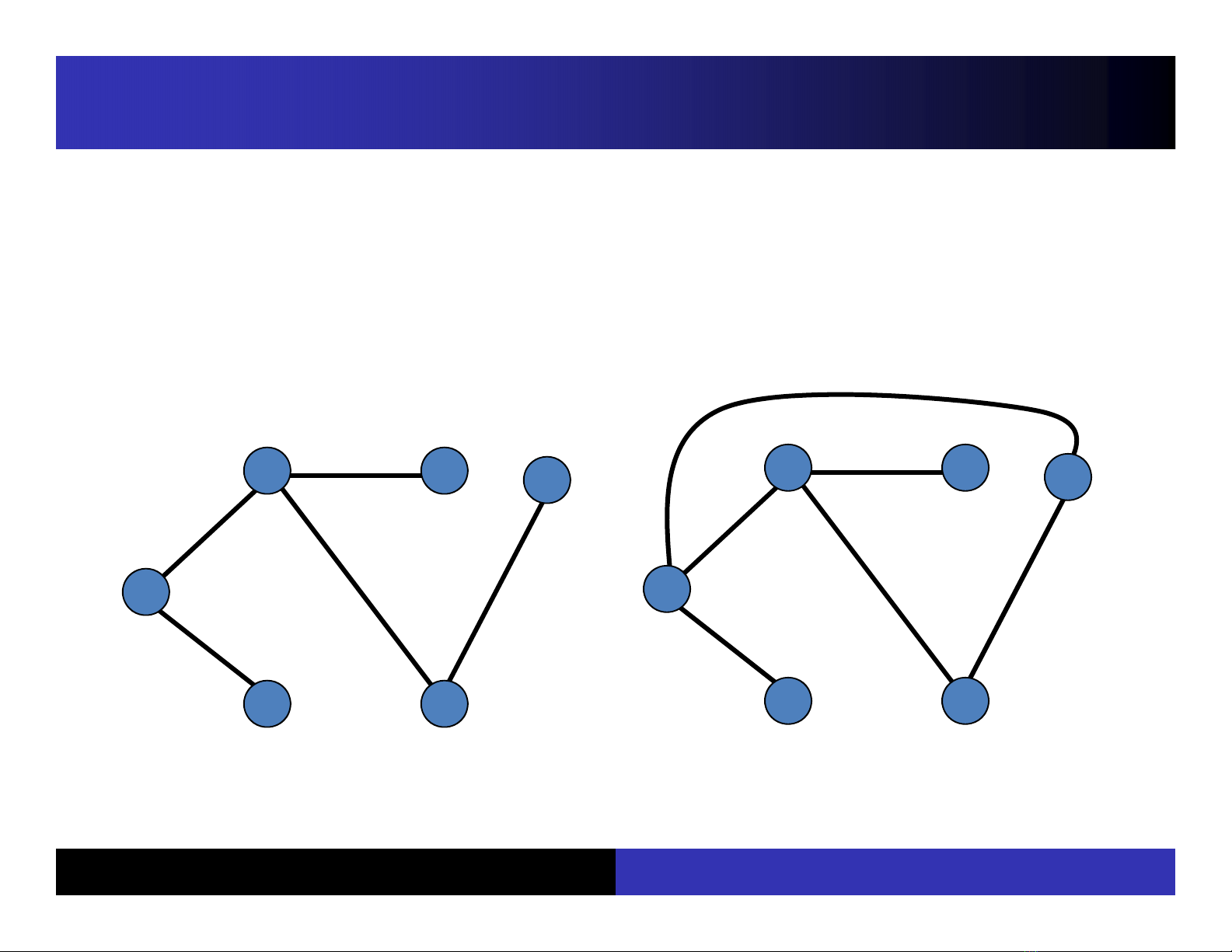
ĐịnhnghĩaCây(Tree):Câylà
Đồthivôhướng,
liênthôngva
khôngcóchutrình
Kháiniệmcây
A
C
B
D
EF
G1
A
C
B
D
EF
G2
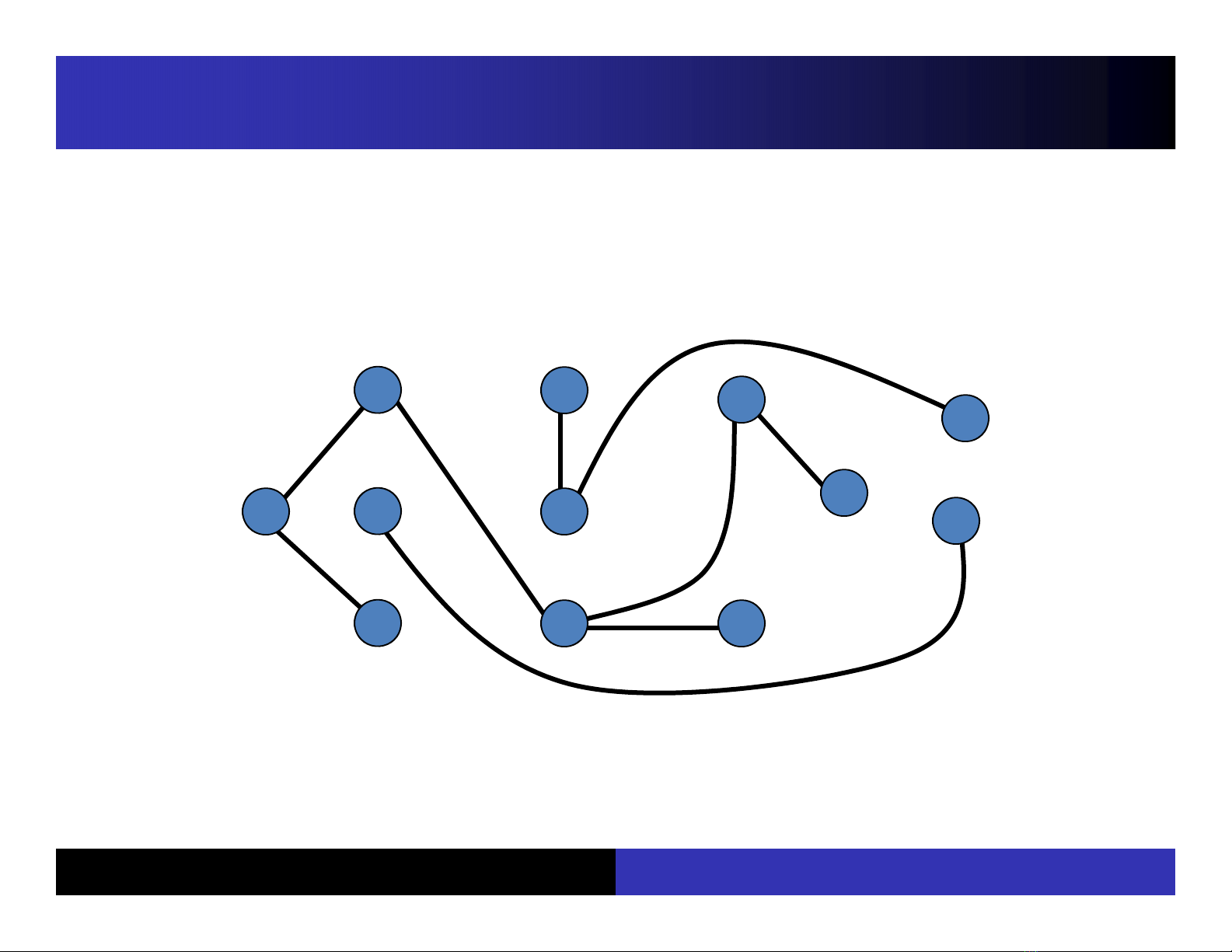
ĐịnhnghĩaRừng(Forest):Rừnglà đồ thị
không có chu trình
Kháiniệmcây
•Nhận xét: Rừng là đồ thị mà mỗi thành phần
liên thông của nó là một cây.
A
D
B
E
GI
H
J
L
K
F
C
Địnhly:ChođồthivôhướngG=(V,E)cónđỉnh.Cácmệnhđề
sautươngđương:
(1) G là 1 cây
(2) G không chứa chu trình và có n-1 cạnh
(3) G liên thông và có n-1 cạnh
(4) G liên thông và mỗi cạnh của nó điều là cầu
(5) Giữa hai đỉnh bất kỳ của G được nối với nhau bởi đúng
một đường đi duy nhất
(6) G không chứa chu trình nhưng khi thêm vào một cạnh ta
thu được đúng một chu trình
CáctínhchấtcơbảncủaCây