BÀI GIẢNG CƠ HỌC KẾT CẤU
CHƯƠNG 6
6.1 CÁC KHÁI NIỆM
Chương 6 : Phương pháp lực 2
1. Hệ siêu tĩnh (HST):
Định nghĩa: Hệ siêu tĩnh là hệ không thể xác định
được toàn bộ phản lực và nội lực nếu chỉ dùng các
phương trình bằng tĩnh học
Cấu tạo hình học: là hệ BBH và có liên kết thừa.
Liên kết thừa là liên kết nhiều hơn số liên kết cần thiết
để hệ có thể bất biến hình
Chữ “thừa” chỉ có ý nghĩa về mặt liên kết
6.1 CÁC KHÁI NIỆM
Chương 6 : Phương pháp lực 3
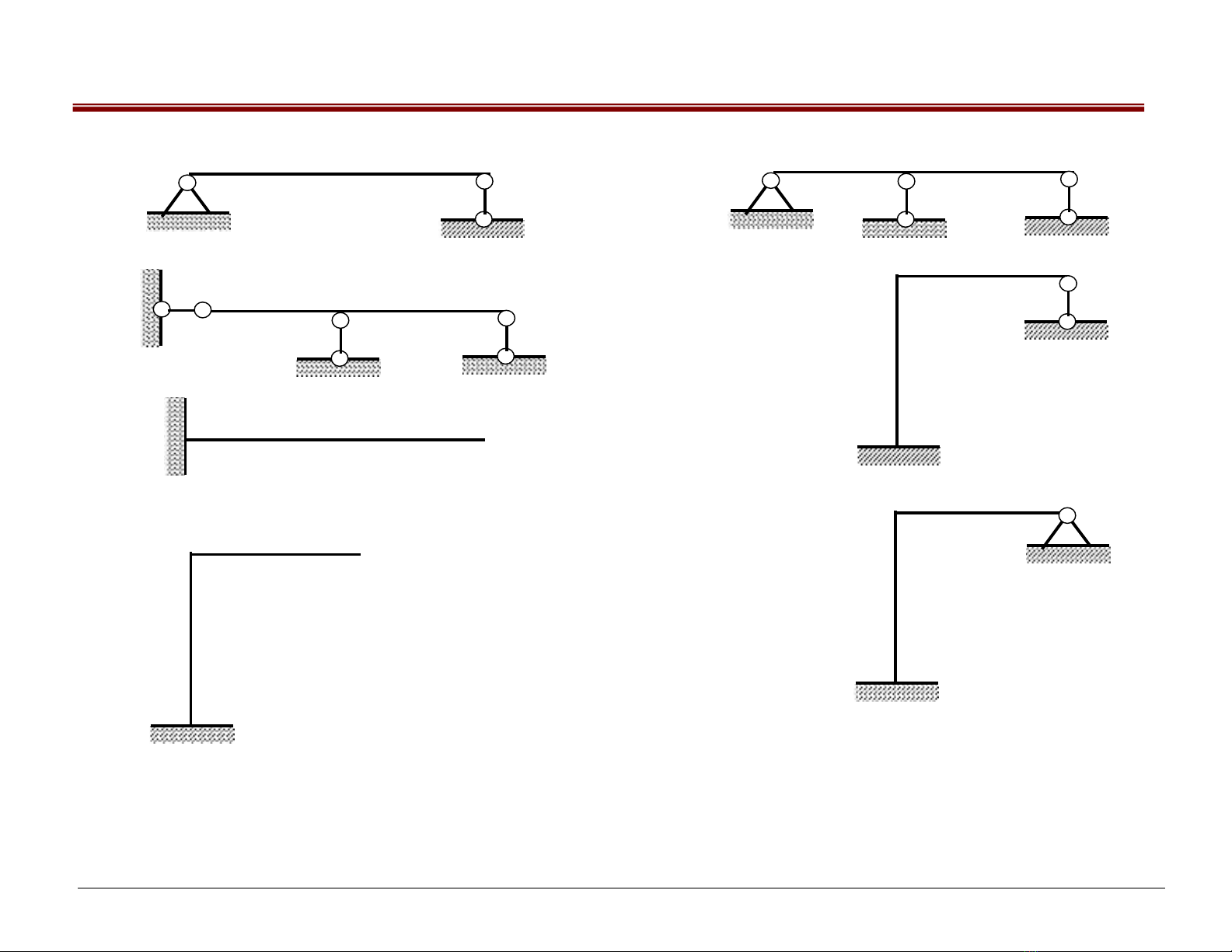
a)
b)
c)
d)
e)
h)
g)
Hình 6.1: a), b), c), d) – Hệ tĩnh định
e), g), h) – Hệ siêu tĩnh
Chương 6 : Phương pháp lực 4
2. Tính chất của HST
- Nội lực và biến dạng nhỏ hơn hệ tĩnh
định tương ứng.
6.1 CÁC KHÁI NIỆM
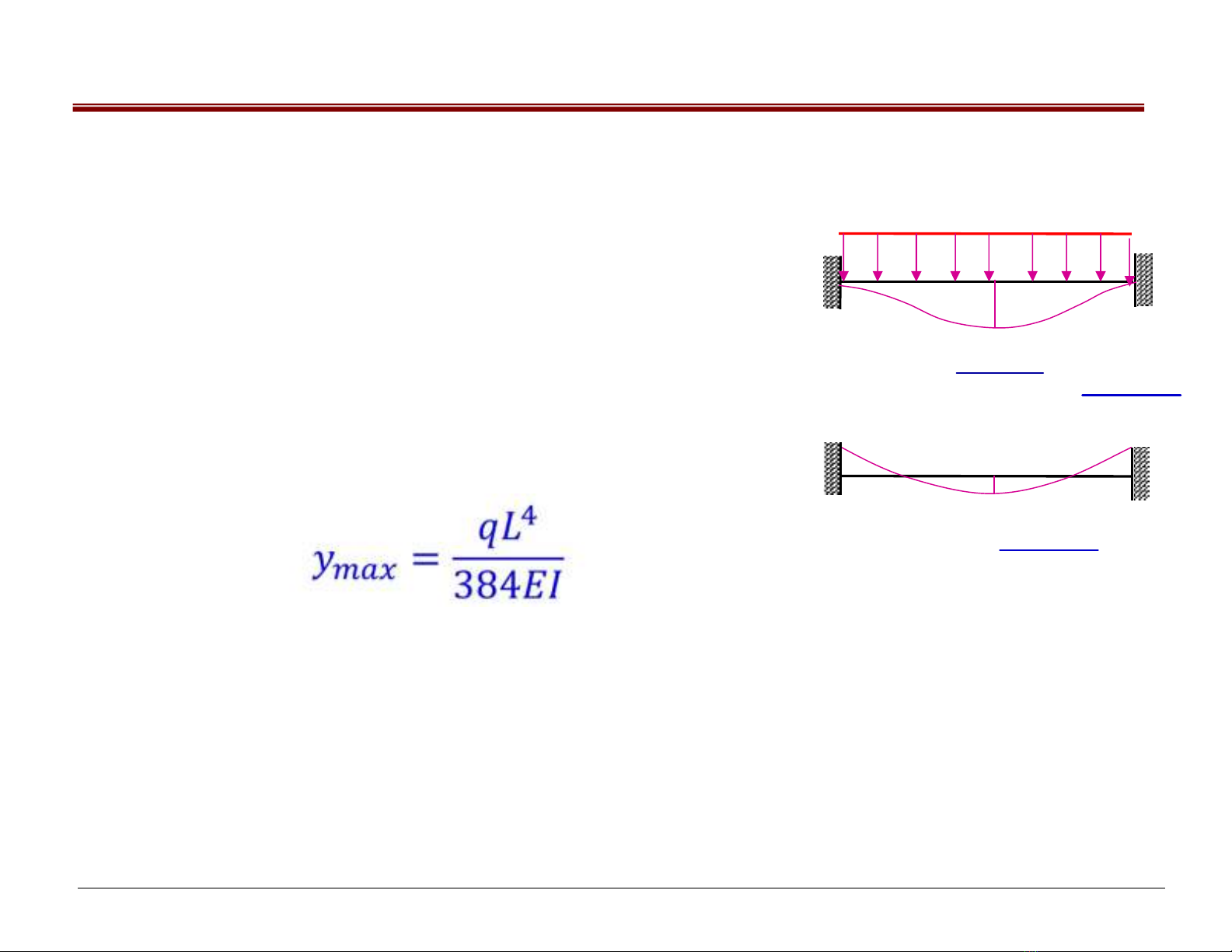
Thí dụ: -Dầm siêu tĩnh (hình 6.2a) có:
+Độ võng lớn nhất ở giữa nhịp
+ Mô men uốn lớn nhất ở ngàm Mmax = qL2 /12 căng thớ trên
+ Mô men uốn ở giữa nhịp M = qL2 /24 căng thớ dưới
4
384
ql
EI
Hình 6.2a
a)
b)
24
qL
2
12
qL
2
q
Chương 6 : Phương pháp lực 5
6.1 CÁC KHÁI NIỆM
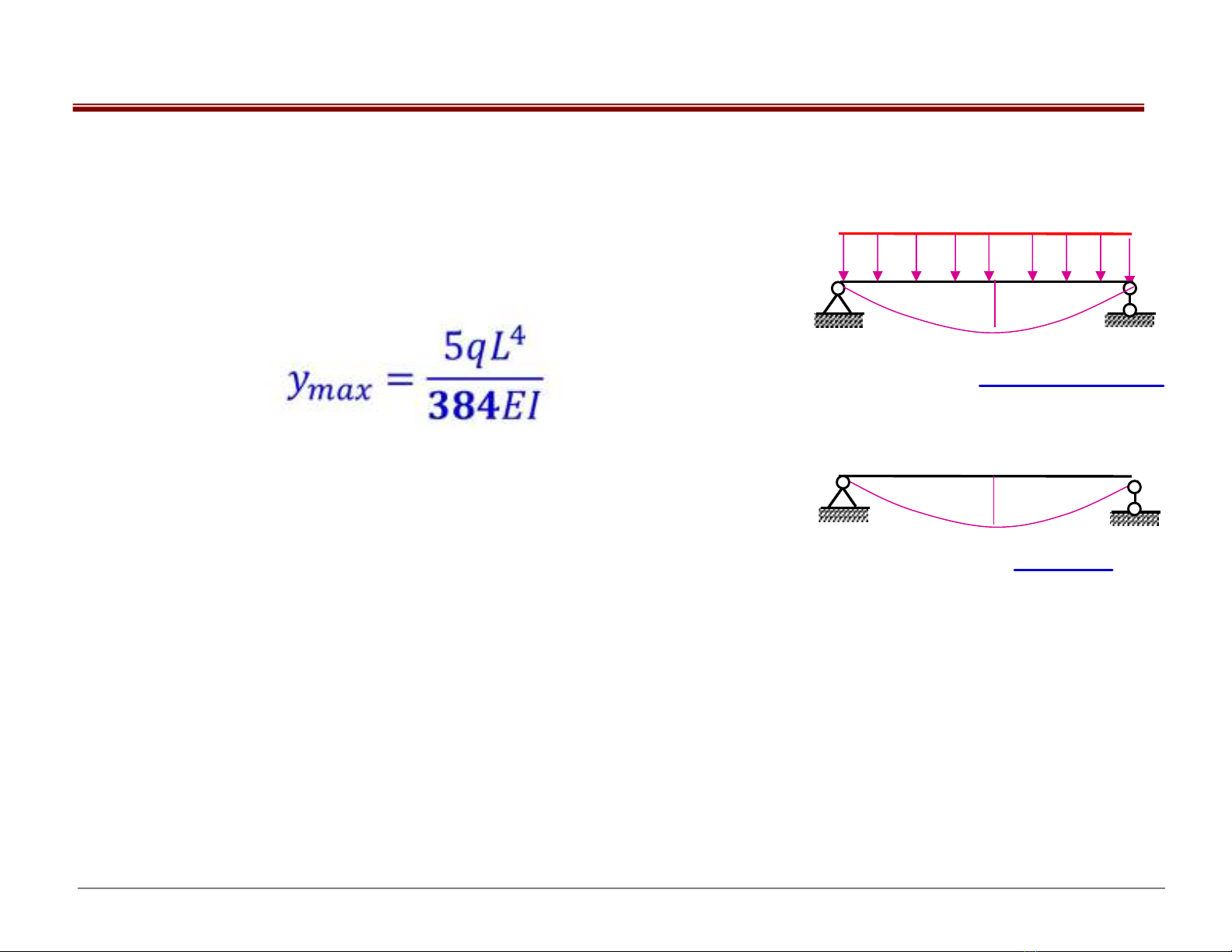
-Dầm tĩnh định (hình 6.2b) có:
+Độ võng lớn nhất ở giữa nhịp
+ Mô men uốn lớn nhất ở giữa
nhịp
Mmax = qL2 /8 căng thớ dưới
Hình 6.2.b
a)
b)
8
qL
2
EI
qL
384
54
q