1
CƠ HỌC KẾT CẤU
Chương 7
PHƯƠNG PHÁP LỰC
Giảng viên: PGS. TS. Cao Văn Vui
7.1. KHÁI NIỆM VỀ HỆ SIÊU TĨNH
Hệ tĩnh định là hệ bất biến hình và đủ liên kế (n=0)
Hệ siêu tĩnh là hệ bất biến hình và có liên kế thừa (n>0)
==>
chỉ với các phương trình cân bằng tĩnh học sẽ không đủ để
giải được tất cả các phản lực hay nội lực trong hệ.
1 Định nghĩa
2
7.1. KHÁI NIỆM VỀ HỆ SIÊU TĨNH
2 Tính chất
Chuyển vị, biến dạng, nội
lực trong hệ siêu tĩnh nói
chung nhỏ hơn trong hệ tĩnh đĩnh cùng kích thước và tải
trọng.
Khi có tải trọng, nhiệt độ, chuyển vị gối tựa,
chế tạo và
lắp ráp không chính xác thì trong hệ siêu tĩnh có nội lực.
Nội lực trong hệ siêu tĩnh phụ thuộc vào
kích thước của
tiết diện trong cấu kiện.
7.1. KHÁI NIỆM VỀ HỆ SIÊU TĨNH
3 Bậc siêu tĩnh
là số liên kết tương đương loại 1 (liên kết thanh)
ngoài số
liên kết cần thiết để hệ bất biến hình.
là trị số n trong các công thức trong chương 2.
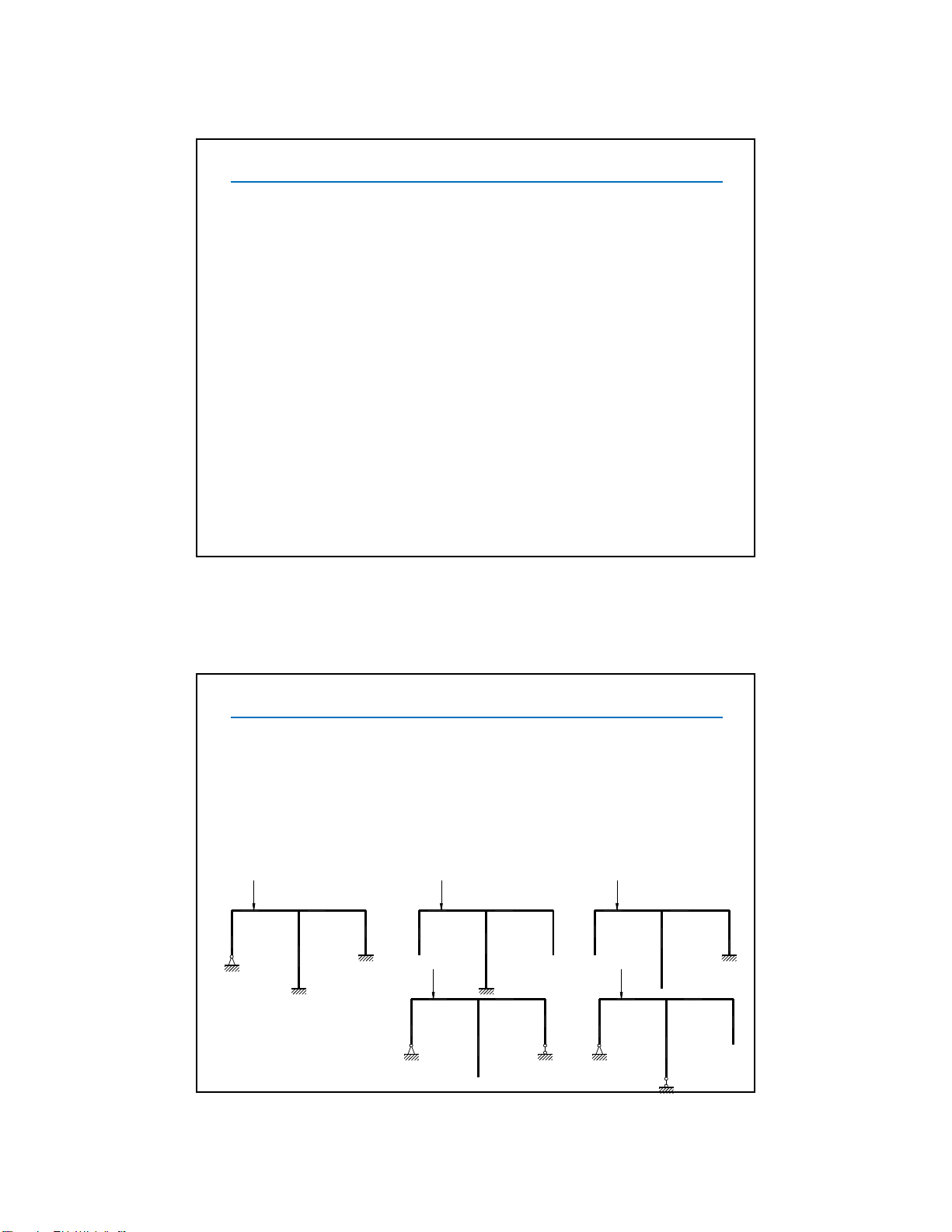
VD:
n = T+2K+C -3D
3
7.2. NỘI DUNG PHƯƠNG PHÁP LỰC
Tính trên hệ cơ bản (=hệ siêu tĩnh –
tất cả hoặc một số
liên kết thừa).
việc giống hệ siêu tĩnh.
7.2. NỘI DUNG PHƯƠNG PHÁP LỰC
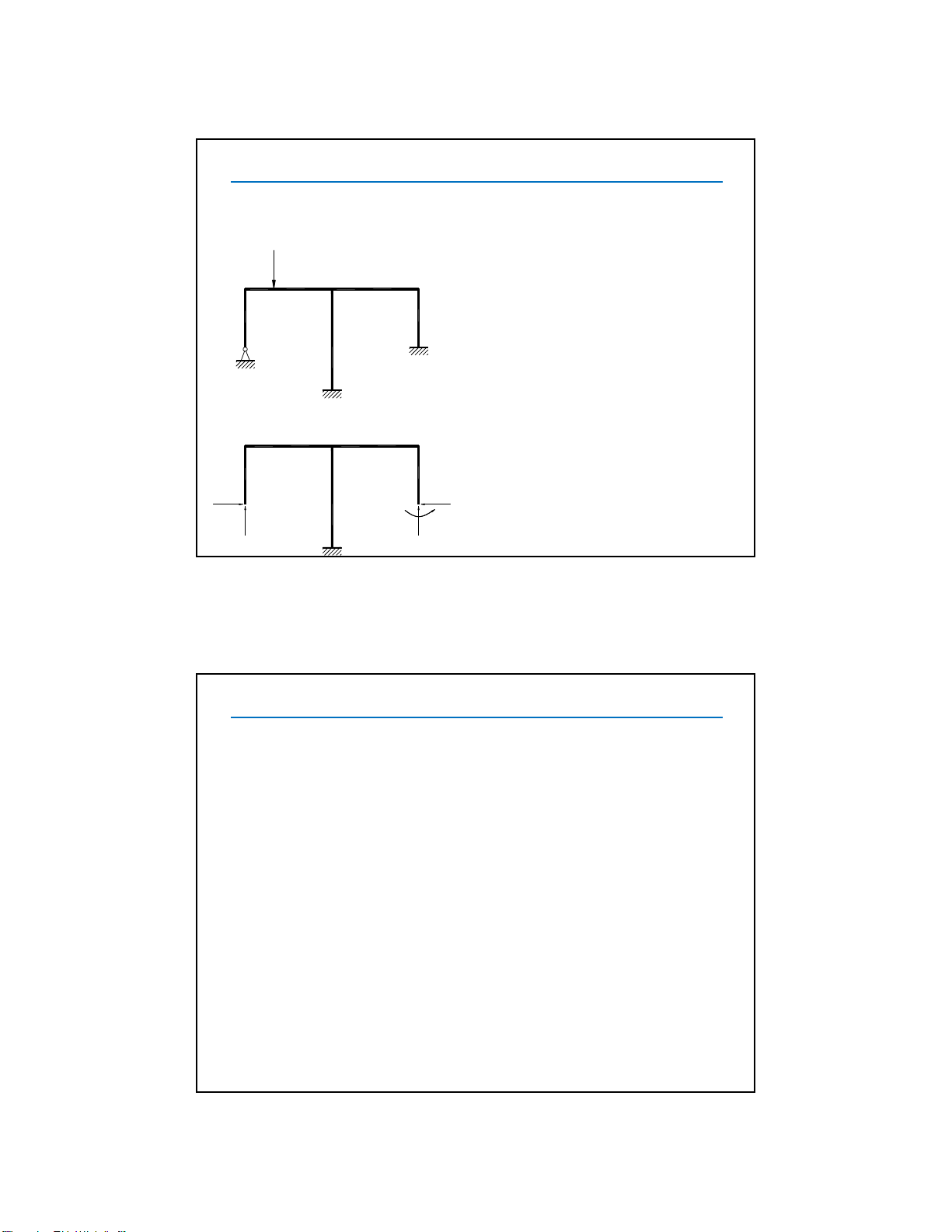
Nếu loại tất cả các liên kết thừa ==> hệ tĩnh định.
Nếu loại một số liên kết thừa ==> hệ siêu tĩnh bậc thấp hơn.
==> có nhiều hệ cơ bản.
Quan trọng là hệ cơ bản phải bất
biến hình và cho phép xác định
được nội lực được dễ dàng.
P P P
P P
4
7.2. NỘI DUNG PHƯƠNG PHÁP LỰC
Xét hệ cơ bản đầu tiên:
X1
P
X2X3
X4
X5
Thay các liên kết đã loại bỏ
bằng các lực X
1
, X
2,
X
3, …
như hình vẽ. Những lực
này (lực tập trung và
mômen) là các ẩn nên được
gọi là phương pháp lực.
Điều kiện để hệ cơ bản
chịu tải trọng và các ẩn lực
là: chuyển vị theo các ẩn
lực phải = 0.
7.2. NỘI DUNG PHƯƠNG PHÁP LỰC
Nếu hệ có n bậc siêu tĩnh (n ẩn), thì ta phải có n điều kiện:
1 1 2
2 1 2
1 2
( , ,..., , , , )
( , ,..., , , , )
( , ,..., , , , )
0
0
...............................
0
n
n
n n
X X X X P t Z
X X X X P t Z
X X X X P t Z
Đây là phương trình cơ bản của phương pháp lực.
Hệ phương
trình này nghiệm đúng với tất cả các hệ (tuân theo hoặc không
tuân theo nguyên lý cộng tác dụng).
Khi tìm được
1 2
, ,...,
n
X X X
, ta xem chúng như là các ngoại lực.
Từ đó ta tìm nội lực như hệ tĩnh định.
5
7.2. NỘI DUNG PHƯƠNG PHÁP LỰC
Phân tích phương trình cơ bản thứ k:
2 1 2 1 2
( , ,..., , , , )
, ,
... ... 0
n k k k k k n k k k
i
X X X X P t Z X X X X X X X X X P X t X Z
X P t Z
 
2 1 2
( , ,..., , , , ) 1 2
, ,
... ... 0
n
i
X X X X P t Z k k kk kn kP kt kZ
X P t Z
 
Trong đó:
km
là chuyển vị theo phương của lực X
k
do X
m
gây ra
trên hệ cơ
bản.
, ,
kP kt kZ
lần lượt là các chuyển vị theo phương của lực X
k
do
tải trọng, nhiệt độ, chuyển vị gối tựa gây ra trên hệ cơ bản.
7.2. NỘI DUNG PHƯƠNG PHÁP LỰC
Nếu gọi
km
là chuyển vị theo phương của lực X
k
do riêng X
m
=1
gây ra trên hệ cơ bản, ta có:
km km m
X
Phương trình trên được viết lại:
1 1 2 2
, ,
... ... 0
i
k k kk k kn n kP kt kZ
X P t Z
X X X X
