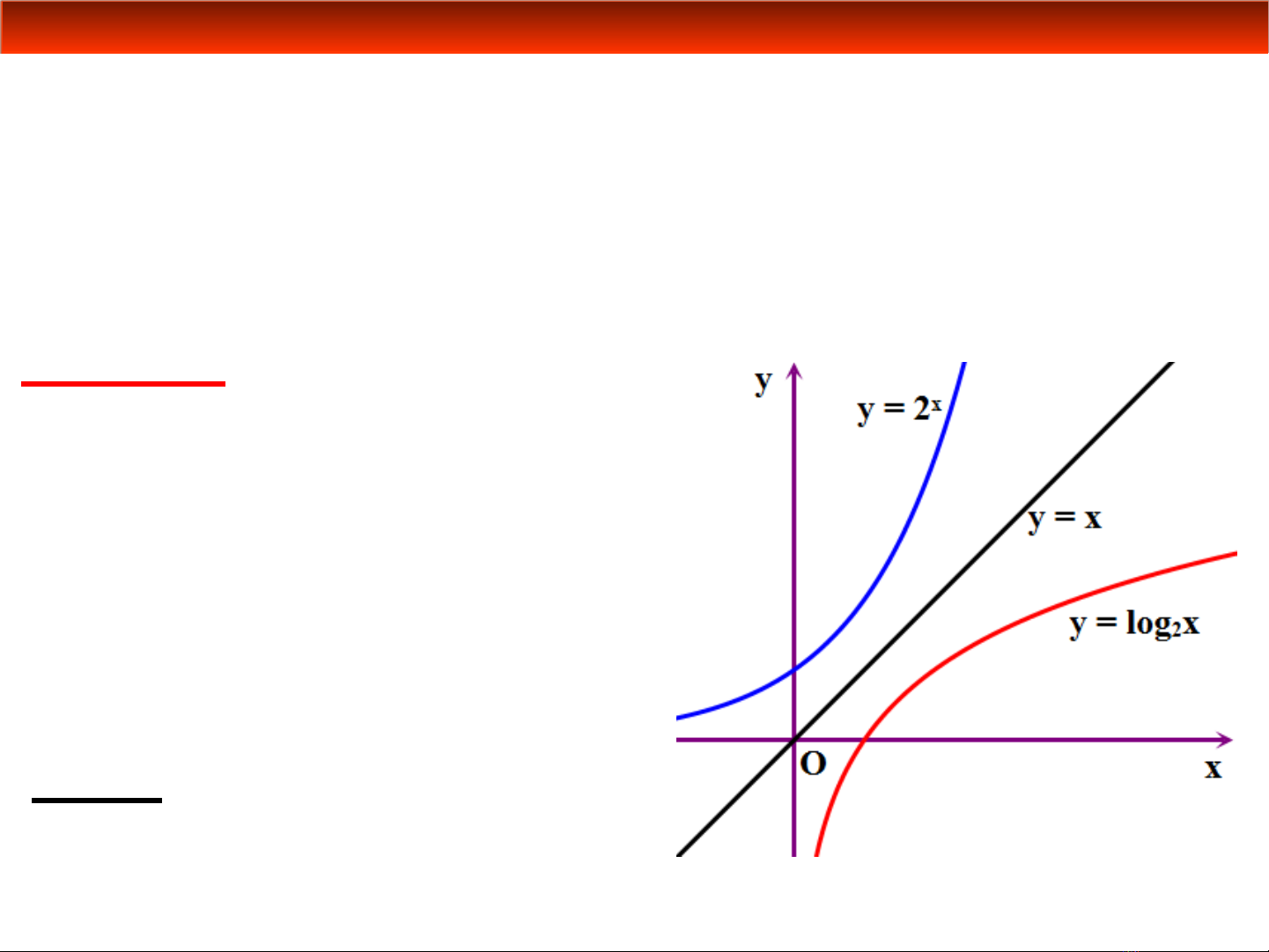
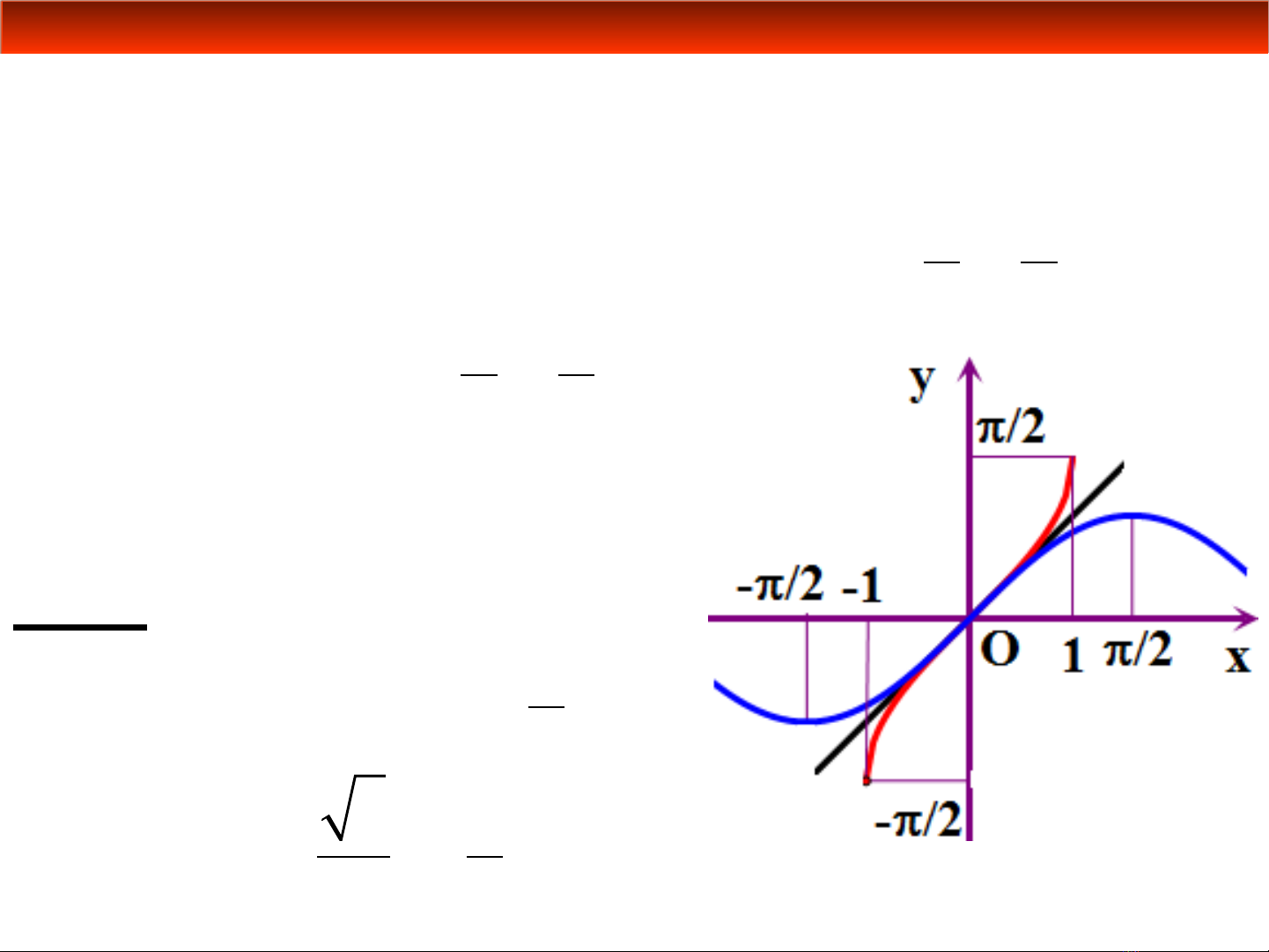
Ch ngA. Hàm s m t bi n sươ ố ộ ế ố
§1. B túc v hàm sổ ề ố
§2. Gi i h n c a hớ ạ ủ àm số
§3. Đi l ng vô cùng bé ạ ượ – vô cùng l nớ
§4. Hàm s liên t cố ụ
…………………………….
§1. B TÚC V HÀM SỔ Ề Ố
1.1. Khái ni m c b nệ ơ ả
1.1.1. Đnh nghĩa hàm sị ố
• Cho
,X Y ¡
khác r ng.ỗ
Ánh x ạ
:f X Y
v i ớ
( )x y f xa
là m t hàm s .ộ ố
Khi đó:
– Mi n xác đnh (MXĐ) c a ề ị ủ f, ký hi u ệDf, là t p ậX.
– Mi n giá tr (MGT) c a ề ị ủ f là:
( )G y f x x X . 1
Ch ng A. Hàm s m t bi n sươ ố ộ ế ố
– N u ế
1 2 1 2
( ) ( )f x f x x x
thì f là đn ánhơ.
– N u ếf(X) = Y thì f là toàn ánh.
– N u ếf v a đn ánh v a toàn ánh thì ừ ơ ừ f là song ánh.
VD 1.
a) Hàm s ố
:f¡ ¡
th a ỏ
( ) 2
x
y f x
là đn ánh.ơ
b) Hàm s ố : [0; )f ¡ th a ỏ
2
( )f x x
là toàn ánh.
c) Hsố
:(0; )f ¡
th a ỏ
( ) lnf x x
là song ánh.
• Hàm s ố
( )y f x
đc g i là hàm ch n n uượ ọ ẵ ế :
( ) ( ), .
f
f x f x x D
• Hàm s ố
( )y f x
đc g i là hàm l n uượ ọ ẻ ế :
( ) ( ), .
f
f x f x x D
2
Ch ng A. Hàm s m t bi n sươ ố ộ ế ố
Nh n xétậ
– Đ tồh c a hàm s ch n đi x ng qua tr c tung.ị ủ ố ẵ ố ứ ụ
– Đ th c a hàm s l đi x ng qua g c t a đ.ồ ị ủ ố ẻ ố ứ ố ọ ộ
1.1.2. Hàm s h pố ợ
• Cho hai hàm s ốf và g th aỏ đi u ki nề ệ
g f
G D.
Khi đó, hàm số ( ) ( )( ) [ ( )]h x f g x f g x o đc g i làượ ọ
hàm s h p c a ố ợ ủ f và g.
Chú ý
( )( ) ( )( ).f g x g f xo o
VD 2. Hàm s ố
2 2 2
2( 1) 1y x x
là hàm h p c a ợ ủ
2
( ) 2f x x x
và
2
( ) 1g x x
. 3
Ch ng A. Hàm s m t bi n sươ ố ộ ế ố
1.1.3. Hàm s ng cố ượ
• Hàm s ốg đc g i là hàm s ng c c a ượ ọ ố ượ ủ f,
ký hi u ệ
1
g f
, n u ế( ),
f
x g y y G .
Nh n xétậ
– Đ th hàm s ồ ị ố
1( )y f x
đi x ngố ứ v iớ đ th ồ ị c a ủ
hàm s ố
( )y f x
qua
đng th ng ườ ẳ
y x
.
VD 3. Cho
( ) 2
x
f x
thì
12
( ) logf x x
, m i ọx > 0.
4
Ch ng A. Hàm s m t bi n sươ ố ộ ế ố
1.2. Hàm s l ng giác ng cố ượ ượ
1.2.1. Hàm s ốy = arcsin x
• Hàm s ố
siny x
có hàm ng c trên ượ
;
2 2
là
1
:[ 1; 1] ;
2 2
f
arcsinx y xa
.
VD 4.
arcsin0 0
;
arcsin( 1) 2
;
3
arcsin 2 3
.
5