Chương 3:
HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
(LÝ THUYẾT TỔNG QUÁT)
Ta đã biết một phương pháp sơ cấp để
giải hệ pttt (pp Gauss). Chương này sẽ
đưa thêm một phương pháp khác để
khảo sát hệ pttt một cách tổng quát
hơn nhờ vào công cụ ma trận và định
thức.
Các vấn đề định tính và định lượng,
chẳng hạn: Khi nào hệ có nghiệm? Có
bao nhiêu nghiệm? Mô tả tập hợp
nghiệm? Tìm nghiệm?Sẽ được giải
đáp trong chương quan trọng này.
Tât nhiên trong thực hành ta có thể kết
hợp nhiều phương pháp để cho kết
quả nhanh chóng và gọn gàng nhất!!
Trước tiên ta xét hai phương pháp là
phương pháp ma trận và phương
pháp định thức để giải một loại hệ đặc
biệt là: Hệ Cramer
§ 1: Phương pháp ma trận và định
thức
1. Hệ Cramer:
Định nghĩa:Hệ Cramer là hệ pttt thỏa
mãn 2 điều kiện:
Số phương trình bằng số ẩn.
Ma trận hệ số không suy biến
(()≠)
Ví dụ:Hãy cho biết hệ sau có là hệ
Cramer?
󰇱
+

+
 +
−
−
+


=
=
=
−
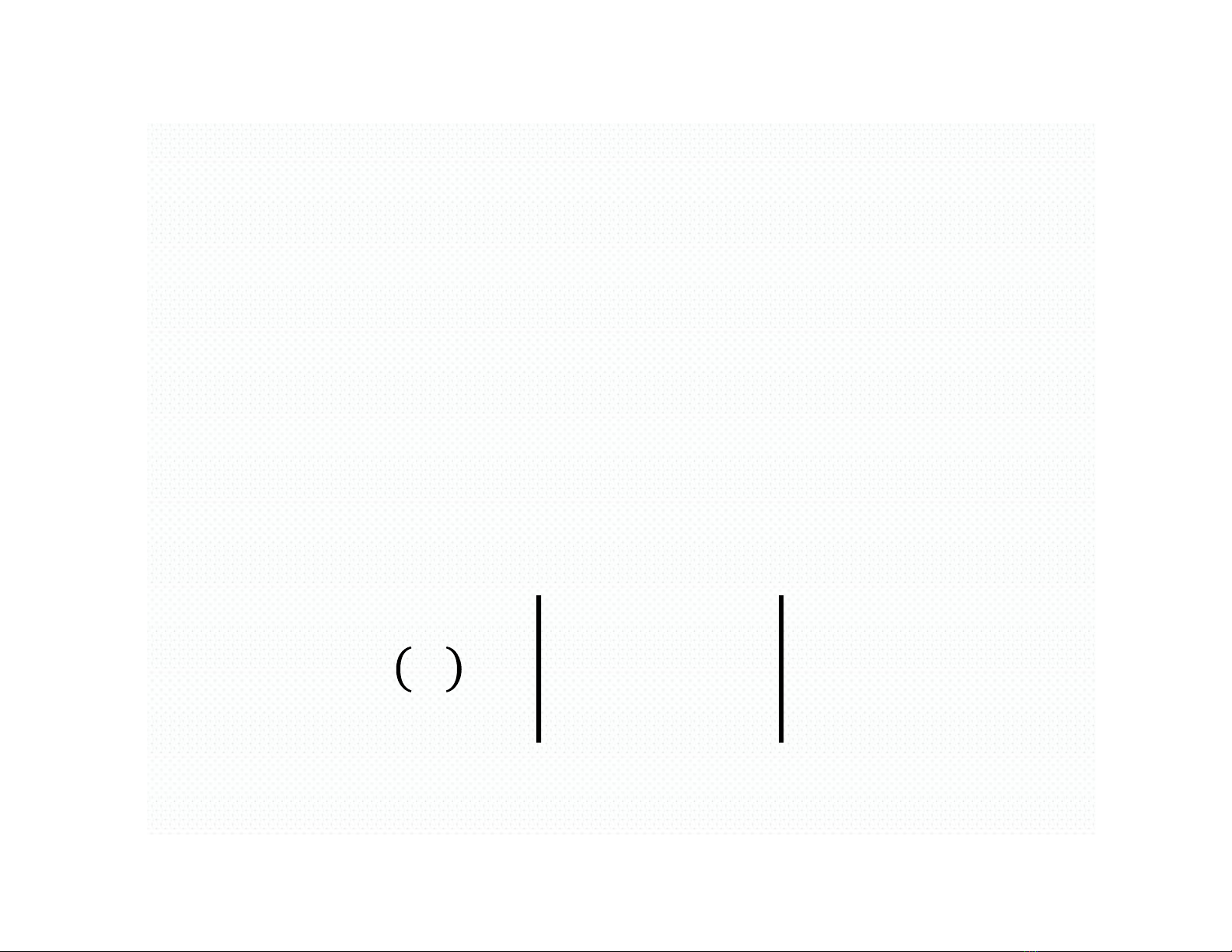
Giải:
Hiển nhiên: số PT = số ẩn (=)
= = −
−
=≠
Vậy hệ đã cho là hệ Cramer.