10/13/2012
1
ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
§1. Khái niệm cơ bản
§2. Đạo hàm riêng – Vi phân
§3. Cực trị của hàm hai biến số
……………………….
§1. KHÁI NIỆM CƠ BẢN
1.1.
Các đ
ịnh nghĩa
a)
Miền phẳng
• Trong mặt phẳng
Oxy
, hình phẳng
D
giới hạn bởi các
đường cong kín được gọi là miền phẳng.
Tập hợp các đường cong kín giới hạn
D
được gọi là
biên của
D
, ký hiệu
D
hay
.
Đặc biệt, mặt phẳng
Oxy
được xem là miền p
hẳng với
biên ở vô cùng.
ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
biếnbiến
• Miền phẳng
D
kể cả biên
D
được gọi là miền đóng
,
miền phẳng
D
không kể biên
D
là miền mở.
• Miền phẳng
D
được gọi là miền liên thông
nếu có 1
đường cong nằm trong
D
nối 2 điểm bất kỳ thuộc
D
.
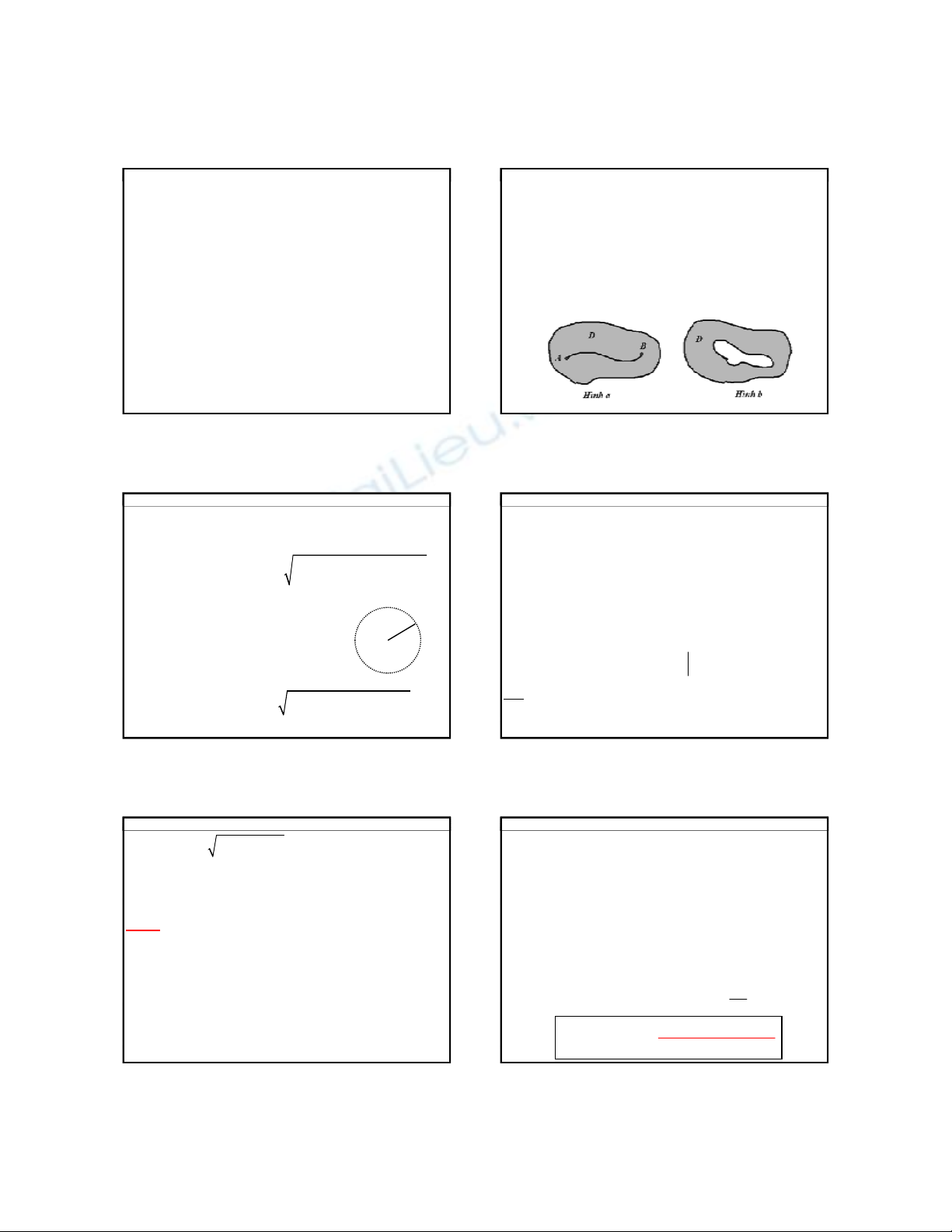
Miền liên thông có biên là 1 đường cong kín được gọi
là miền đơn liên (hình a)
; có biên là nhiều đường cong
kín rời nhau là miền đa liên (hình b).
ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
b) Lân cận của một điểm
• Khoảng cách giữa 2 điểm
111
(,)
Mxy
,
222
(,)
Mxy
là:
22
12121212
,
dMMMMxxyy
 .
• Hình tròn
(,)
SM
mở có tâm
(,)
Mxy
, bán kính
0

được
gọi là một
lân cận
của điểm
M
.
Nghĩa là:
22
00000
(,)(,)()()MxySMxxyy

.
M
•
ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
biếnbiến
c) Hàm số hai biến số
• Trong mặt phẳng
Oxy
cho tập
2
D
¡
.
Tương ứng
:
fD
¡
cho tương ứng mỗi
(,)
xyD
với một giá trị
(,)
zfxy

¡
duy nhất
được gọi là
hàm số hai biến số
,
xy
.
• Tập
2
D
¡
được gọi là miền xác định (MXĐ) của h
àm
số, ký hiệu
f
D
. Miền giá trị của hàm số là:
(,)(,)
f
GzfxyxyD
¡.
VD
• Hàm số
2
(,)3cos
fxyxyxy
 có
2
f
D
¡
.
ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
• Hàm số
22
4
zxy

có MXĐ là hình tròn đóng
tâm
(0;0)
O
, bán kính
2
R
.
• Hàm số
22
ln(4)
zxy

có MXĐ là hình tròn mở
tâm
(0;0)
O
, bán kính
2
R
.
Chú ý
• Trong trường hợp xét hàm số
(,)
fxy
mà không nói gì
thêm thì ta hiểu MXĐ của hàm số là tập tất cả các điểm
2
(,)Mxy
¡
sao cho
(,)
fxy
có nghĩa.
• Hàm có nhiều hơn hai biến được định nghĩa tương tự.
1.2.
Giới hạn của hàm số hai biến
s
ố
(
xem giáo trình
)
1.3.
Hàm số liên tục
(
xem giáo trình
)
ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
biếnbiến
§2. ĐẠO HÀM RIÊNG
–
VI PHÂN
2.1. Đạo hàm riêng
a) Đạo hàm riêng cấp 1
• Cho hàm số
(,)
fxy
xác định trên miền mở
2
D
¡
chứa điểm
000
(,)
Mxy
. Cố định
0
y
, nếu hàm số
0
(,)
fxy
có đạo hàm tại
0
x
thì ta gọi đạo hàm đó là
đạo hàm riêng
theo biến
x
của hàm số
(,)
fxy
tại
00
(,)
xy
.
Ký hiệu:
00
(,)
x
fxy
hay
/
00
(,)
x
fxy
hay
00
(,).
f
xy
x
Vậy
0
/
000
00
0
(, )(, )
(,)lim.
xxx
fxyfxy
fxy
xx
10/13/2012
2
ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
Chú ý
• Nếu
()
fx
là hàm số một biến
x
thì /
x
fdf
f
xdx

.
•
Hàm số nhiều hơn hai biến có định nghĩa t
ương tự
.
• Tương tự, đạo hàm riêng
theo biến
y
tại
00
(,)
xy
là:
0
/
000
00
0
(, )(, )
(,)lim.
yyy
fxyfxy
fxy
yy
ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
biếnbiến
VD 1. Tính các đạo hàm riêng của hàm số:
4323
(,)323
fxyxxyyxy
 tại
(1;2)
.
Giải.
/322/
(,)493(1;2)46
xx
fxyxxyyf

.
/32/
(,)663(1;2)39
yy
fxyxyyxf.
VD 2. Tính các đạo hàm riêng của
2
22
1
ln
1
x
z
xy

.
Giải. Ta có
222
ln(1)ln(1)
zxxy

. Suy ra:
/
222
22
11
x
xx
z
xxy


, /
22
2
1
y
y
z
xy


.
ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
VD 3. Tính các đạo hàm riêng của
cos
x
z
y
tại
(; 4)
.
Giải
/
/ /
12
sinsin(;4)
8
xx
x
xxx
zz
yyyy



,
/
/ /
2
2
sinsin(;4)
32
yy
y
xxxx
zz
yyy
y


 .
ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
biếnbiến
VD 4. Tính các đạo hàm riêng của
2
(,,)sin
xy
fxyzez
.
Giải.
22
/2/
()sin2sin
xyxy
xx
fxyezxyez

22
/2/ 2
()sinsin
xyxy
yy
fxyezxez

2
/
cos
xy
z
fez
.
ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
b) Đạo hàm riêng cấp cao
• Đạo hàm riêng (nếu có) của hàm số
/
(,)
x
fxy
,
/
(,)
y
fxy
được gọi là các
đạo hàm riêng cấp hai
của
(,)
fxy
.
Ký hiệu:
2
2
2
x
xxx
x
f
fff
x
f
xx



 
,
2
2
2
y
yyy
y
f
fff
y
f
yy



 
,
2
xyxyy
x
f
ff
yx
f
f
yx




,
2
yxyxx
y
f
ff
xy
f
f
xy




.
ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
biếnbiến
•
Hàm số nhiều hơn 2 biến và đạo hàm riêng cấp cao hơn
2 có định nghĩa t
ương tự
.
VD 5. Tính các đạo hàm riêng cấp hai của hàm số:
3234
(,)
y
fxyxexyy

tại
(1; 1)
.
Giải. Ta có
/23
/3223
32
34
y
x
y
y
fxexy
fxexyy


10/13/2012
3
ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
2
2
/ / 3
//22/ /
/ /
322
62
36
612
y
x
y
xyyx
y
y
fxey
fxexyf
fxexyy



2
2
/ /
/ /
/ /
(1;1)62
(1;1)36
(1;1)6.
x
xy
y
fe
fe
fe



ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
biếnbiến
VD 6. Cho hàm số
5445
(,)
fxyxyxy
 .
Giá trị của đạo hàm riêng cấp năm 32
(5)
(1;1)
xy
f
là:
A. 32
(5)
(1;1)480
xy
f ; B. 32
(5)
(1;1)480
xy
f ;
C. 32
(5)
(1;1)120
xy
f ; D. 32
(5)
(1;1)120
xy
f .
Giải.
/435
54
x
fxxy

2
/ /
325
2012
x
fxxy

3
// /
25
6024
x
fxxy
 3
(4)
4
120
xy
fxy

32
(5)
3
480
xy
fxy
 32
(5)
(1;1)480.
xy
fA

ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
• Định lý Schwarz
Nếu hàm số
(,)
fxy
có các đạo hàm riêng
xy
f

và
yx
f

liên tục trong miền mở
2
D
¡
thì
xyyx
ff

.
Hermann Amandus Schwarz
(1843 – 1921)
ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
biếnbiến
VD 7. Đạo hàm riêng 22
()
(2)
mn
mn
xyx
zm
của
2
xy
ze
là:
A.
2
(1)2
nmnxy
e

; B.
2
(1)2
mmnxy
e

;
C.
2
(1)2
mmxy
e
; D.
2
(1)2
nmxy
e
.
Giải. Ta có 22
()()
mnmn
mnmn
xyxxy
zz

.
/ 2
2
xy
x
ze
2
/ /
22
2...
xy
x
ze

()
2
2
m
m
mxy
x
ze

2
(1)(2)
22
22
mm
mm
mxymxy
xyxy
zeze



()
2
(1)2
mn
mn
nmxy
xy
zeD

.
ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
2.2. V
I PHÂN
2.2.1.
Vi phân cấp 1
a) Số gia của hàm số
• Cho hàm số
(,)
fxy
xác định trong lân cận
0
(,)
SM
của điểm
000
(,)
Mxy
. Cho
x
một số gia
x
và
y
một
số gia
y
, khi đó hàm
(,)
fxy
có tương ứng số gia:
0000
(, )(, ).
ffxxyyfxy

ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
biếnbiến
b) Định nghĩa
• Nếu trong lân cận
0
(,)
SM
với số gia
x
,
y
mà số
gia
f
tương ứng có thể viết được dưới dạng
22
()(.
)
.,fAxByOr
rxy
 
trong đó
,
A B
là những số
chỉ phụ thuộc vào điểm
000
(,)
Mxy
và hàm
(,)
fxy
, không phụ thuộc
,
xy

thì đại lượng
..
AxBy

được gọi là vi phân
của hàm
số
(,)
fxy
tại điểm
000
(,)
Mxy
.
• Khi đó,
(,)
fxy
được gọi là khả vi tại điểm
000
(,)
Mxy
.
Ký hiệu:
...
dfAxBy

10/13/2012
4
ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
Nhận xét
• Xét những điểm
00
(, )
Mxxyy

dịch chuyển
trên đường đi qua
0
M
song song
Ox
. Khi đó
0
y

:
0000
(, )(, ).()
ffxxyfxyAxOx

/
00
0
lim(,)
x
x
f
AAfxy
x


.
Tương tự,
/
00
0
lim(,)
y
y
f
BBfxy
y


.
Suy ra
/ /
(, )(, ).(, ).
xy
dfxyfxyxfxyy

.
• Xét
(, )(,)
fxyxdfxyxdxx

.
Tương tự,
dyy

.
Vậy
(, )(, )(, ).
xy
dfxyfxydxfxydy


ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
biếnbiến
c) Định lý
• Nếu hàm số
(, )
fxy
có các đạo hàm riêng
trong lân cận
nào đó của
00
(,)
xy
và các đạo hàm riêng này
liên tục
tại
00
(,)
xy
thì
(, )
fxy
khả vi tại
00
(,)
xy
.
VD 8. Cho hàm
25
(,)
xy
fxyxey

. Tính
(1;1)
df
.
Giải.
/2/ 2
/24/ 2
(2)(1;1)3
5(1;1)5
xy
xx
xy
yy
fxxefe
fxeyfe











.
Vậy
22
(1;1)3(5)
dfedxedy

.
ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
VD 9. Tính vi phân cấp 1 của hàm
2
2
sin()
xy
zexy
.
Giải.
2
/222
2sin()cos()
xy
x
zxxyyxye




,
2
/22
sin()2cos()
xy
y
zxyxyxye




.
Vậy
2
222
2sin()cos()
xy
dzxxyyxyedx




2
22
sin()2cos()
xy
xyxyxyedy




.
ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
biếnbiến
2.2.2. Vi phân cấp 2
• Giả sử
(,)
fxy
là hàm khả vi với
,
xy
là các biến độc
lập. Các số gia
,
dxxdyy

tùy ý độc lập với
,
xy
nên được xem là hằng số đối với
,
xy
. Vi phân của
(,)
dfxy
được gọi là vi phân cấp 2 của
(,)
fxy
.
Ký hiệu và công thức:
22
222
2.
xy
xy
dfddffdxfdxdyfdy


Chú ý
• Nếu
,
xy
là các biến không độc lập (biến trung gian)
(,)
xx

,
(,)
yy

thì công
thức trên không còn
đúng nữa. Sau đây ta chỉ xét trường hợp
,
xy
độc lập.
ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
VD 10. Cho hàm số
23235
(,)3
fxyxyxyxy
 .
Tính vi phân cấp hai
2
(2;1)
df
.
Giải. Ta có:
/3225
/2234
29
3215
x
y
fxyyxy
fxyxyxy


22
22
/// /
35
//224/ /
/// /
233
218(2;1)34
6+245(2;1)170
6+260(2;1)460.
xx
xyxy
yy
fyxyf
fxyyxyf
fxyxxyf
















Vậy
222
(2;1)34340460
dfdxdxdydy

.
ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
biếnbiến
VD 11. Tính vi phân cấp 2 của hàm
2
(,)ln()
fxyxy
.
Giải. Ta có
2
/ /
22
122
,
xy
yxy
ff
xy
xyxy

22
/// /
/ /
22
12
,0,
xy
xy
fff
xy
 .
Vậy
22222
2
dfxdxydy


.
10/13/2012
5
ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
2.3. Đạo hàm của hàm số ẩn (hai biến)
• Hàm
(,)
zxy
xác định trên
2
z
D
¡
thỏa
phương trình
(,,(,))0,(,)
z
FxyzxyxyDD

(*) được gọi là
hàm số ẩn
hai biến xác định bởi (*)
.
Giả sử các hàm trên đều khả vi, đạo hàm 2 vế (*) ta được:
.0,.0
xzxyzy
FFzFFz


.
Vậy
,0.
y
x
xyz
zz
F
F
zzF
FF



ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
biếnbiến
Giải.
Ta có
(,,)cos()
Fxyzxyzxyz

/
/
/
sin()
sin()
sin().
x
y
z
Fyzxyz
Fxzxyz
Fxyxyz



Vậy /
sin()
sin()
x
yzxyz
z
xyxyz



,
/
sin()
sin()
y
xzxyz
z
xyxyz



.
VD 12. Cho hàm ẩn
(,)
zxy
thỏa phương trình:
cos()
xyzxyz

. Tính
/ /
,
xy
zz
.
ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
Giải. Ta có
222
2462
Fxyzxyz

/
/
/
24
2
3
26
y
y
z
Fy y
zz
Fz



.
VD 13. Cho hàm ẩn
(,)
zxy
thỏa phương trình mặt cầu:
222
24620
xyzxyz

. Tính
/
y
z
.
ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
biếnbiến
§3. CỰC TRỊ CỦA HÀM HAI BIẾN SỐ
3.1. Định nghĩa
• Hàm số
(,)
zfxy
đạt cực trị thực sự tại
000
(,)
Mxy
nếu với mọi điểm
(,)
Mxy
khá gần nhưng khác
0
M
thì
hiệu
00
(,)(,)
ffxyfxy

có dấu không đổi.
• Nếu
0
f

thì
00
(,)
fxy
là giá trị cực tiểu và
0
M
là
điểm cực tiểu của
(,)
zfxy
.
• Nếu
0
f

thì
00
(,)
fxy
là giá trị cực đại và
0
M
là
điểm cực đại của
(,)
zfxy
.
ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
VD 1. Hàm số
2
2
22
3
(,)
24
yy
fxyxyxyx



2
(,)0,(,)fxyxy
¡
nên đạt cực tiểu tại
(0;0)
O
.
ChươngChương
6. 6.
PhépPhép
tín ht ính
vi vi
phânphân
hàmhàm
haihai
biếnbiến
3.2. Đ
ỊNH LÝ
a) Điều kiện cần
• Nếu hàm số
(,)
zfxy
đạt cực trị tại
000
(,)
Mxy
và
tại đó hàm số có đạo hàm riêng thì:
/ /
0000
(,)(,)0.
xy
fxyfxy

• Điểm
000
(,)
Mxy
thỏa
/ /
0000
(,)(,)0
xy
fxyfxy

được
gọi là
điểm dừng
,
0
M
có thể không là điểm cực trị.