118
C5. HÀM NHIỀU BIẾN
1. MỘT SỐ KHÁI NIỆM CƠ BẢN
Không gian n chiều: Một bộ gồm n số thực được sắp xếp
thứ tự, ký hiệu (x1, x2,… xn) (xiR, i = 1,.. n) được gọi là
một điểm n - chiều. Tập hợp các điểm n - chiều được ký
hiệu là Rn.
Rn= {x = (x1, x2,… xn): xiR, i = 1,.. n}
Trong đó xilà toạ độ thứ i của điểm x.
119
C5. HÀM NHIỀU BIẾN
Khoảng cách 2 điểm:
x = (x1,x2,… xn), y = (y1,y2,… yn) Rn:
n
i
ii yxyxd
1
2
)(),(
Lân cận: Cho x0Rnvà số r > 0.
Tập S(x0, r) = {x Rn: 0 < d(x,x0) < r}
được gọi là một lân cận của x0.
120
C5. HÀM NHIỀU BIẾN
Điểm biên: Điểm x0Rnđược gọi là điểm biên của D
Rnnếu mọi lân cận của x0đều chứa ít nhất các điểm x, y:
x D, y D. Tập hợp mọi điểm biên của D được gọi là
biên của D.
Điểm trong: Điểm x0Rnđược gọi là điểm trong của D
Rnnếu D chứa một lân cận của x0.
Tập đóng: Nếu biên của D thuộc D.
Tập mở: Nếu biên của D không thuộc D.
121
C5. HÀM NHIỀU BIẾN
Hàm 2 biến: D R2, một ánh xạ f: D R, được gọi là hàm
số 2 biến. Ký hiệu:
)
,
(
)
,
(
:
y
f
z
y
f
• D: miền xác định
• f(D) = {zD: z = f(x,y), (x,y) D} gọi là miền giá trị
Ví dụ: Tìm miền xác định:
z = 2x – 3y +5
z = ln(x + y -1)
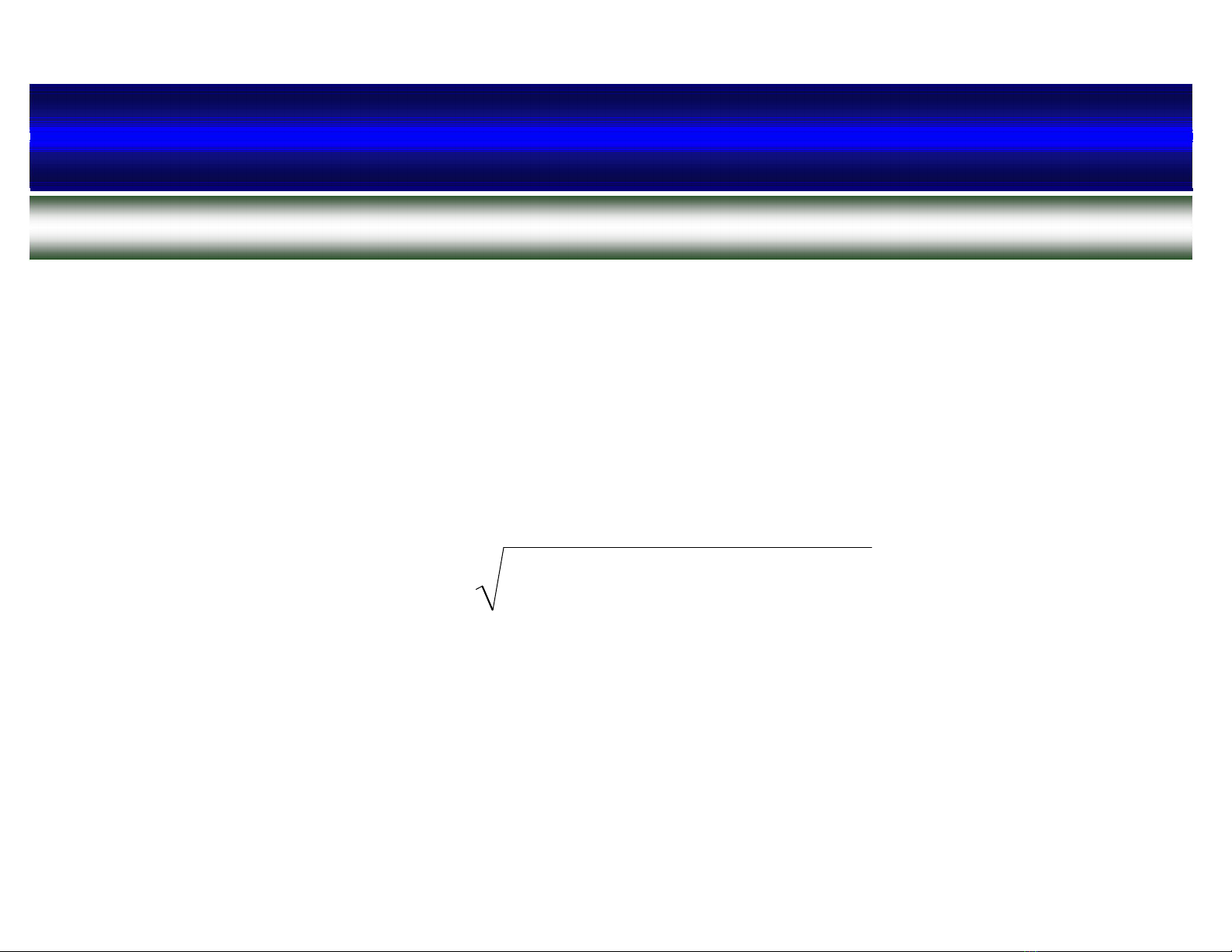
22
1yxz
Hàm n biến: D Rn, một ánh xạ f: D R được gọi là hàm
số n biến. Ký hiệu:
)
,...
,
(
)
,...
,
(
:
2
1
2
1
n
n
f
z
f
122
C5. HÀM NHIỀU BIẾN
2. GIỚI HẠN VÀ TÍNH LIÊN TỤC CỦA HÀM SỐ
Giới hạn hàm số: Cho hàm f(x,y) xác định tại lân cận
M0(x0,y0), có thể không xác định tại M0. Số thực L được gọi
là giới hạn của f khi M(x,y) tiến đến M0(x0,y0), nếu:
 > 0,  > 0: d(M,M0) < => f(M) – L<
2
0
2
0
0
)y-(y)x-(x)Md(M,
L
M
f
MM
)
(
lim
0
L
y
x
f
yxyx
)
,
(
lim
),(),(
0
0
L
y
f
yy
xx
)
,
(
lim
0
0