HÀM
NHIỀU BIẾN CHƯƠNG 3
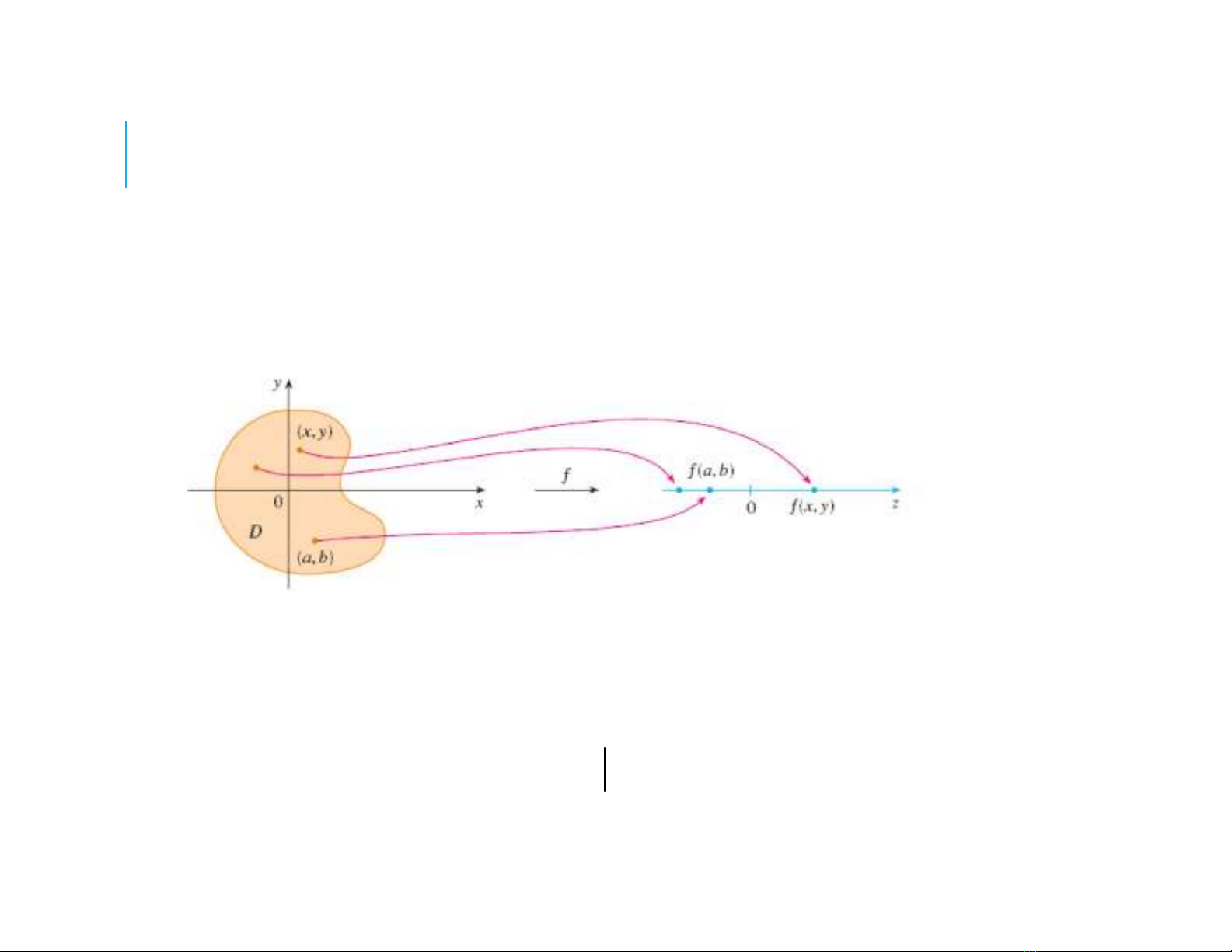
KHÁI NIỆM HÀM HAI BIẾN
Định nghĩa: Cho không gian:
Ánh xạ:
Được gọi là hàm hai biến xác định trên tập hợp D
Mỗi cặp (x,y)∈ tương ứng với một số thực z
x, y là các biến độc lập; z là biến phụ thuộc
( ) ( )
:
, ,
f D R
x y z f x y
®
=a
( )
{
}
2 2
, : ,
R x y x y R va D R
= Î Ì
KHÁI NIỆM HÀM HAI BIẾN
Mỗi cặp (x,y)∈ tương ứng với một số thực z
x, y là các biến độc lập; z là biến phụ thuộc
Tập D là miền xác định (domain)
Miền giá trị (range) của hàm f
, ,
T f x y x y D
TẬP XÁC ĐỊNH HÀM HAI BIẾN
Khái niệm. Tập xác định của hàm số là tập hợp tất cả các
cặp (x,y) sao cho giá trị biểu thức f(x,y) là số thực.
Ví dụ 1. Với
2
D
=
¡
và
3 2
( , ) .
f x y x x xy
Miền xác định của hàm số là cả không gian
2
.
¡
Ứng với cặp số
( , ) (2, 1)
x y D
, ta có
3 2
(2, 1) 2 ( 1) 2.( 1) 5
z f
Ứng với cặp số
( , ) (3,2) ,
x y D
ta có
3 2
(3,2) 3 2 3.2 29.
z f
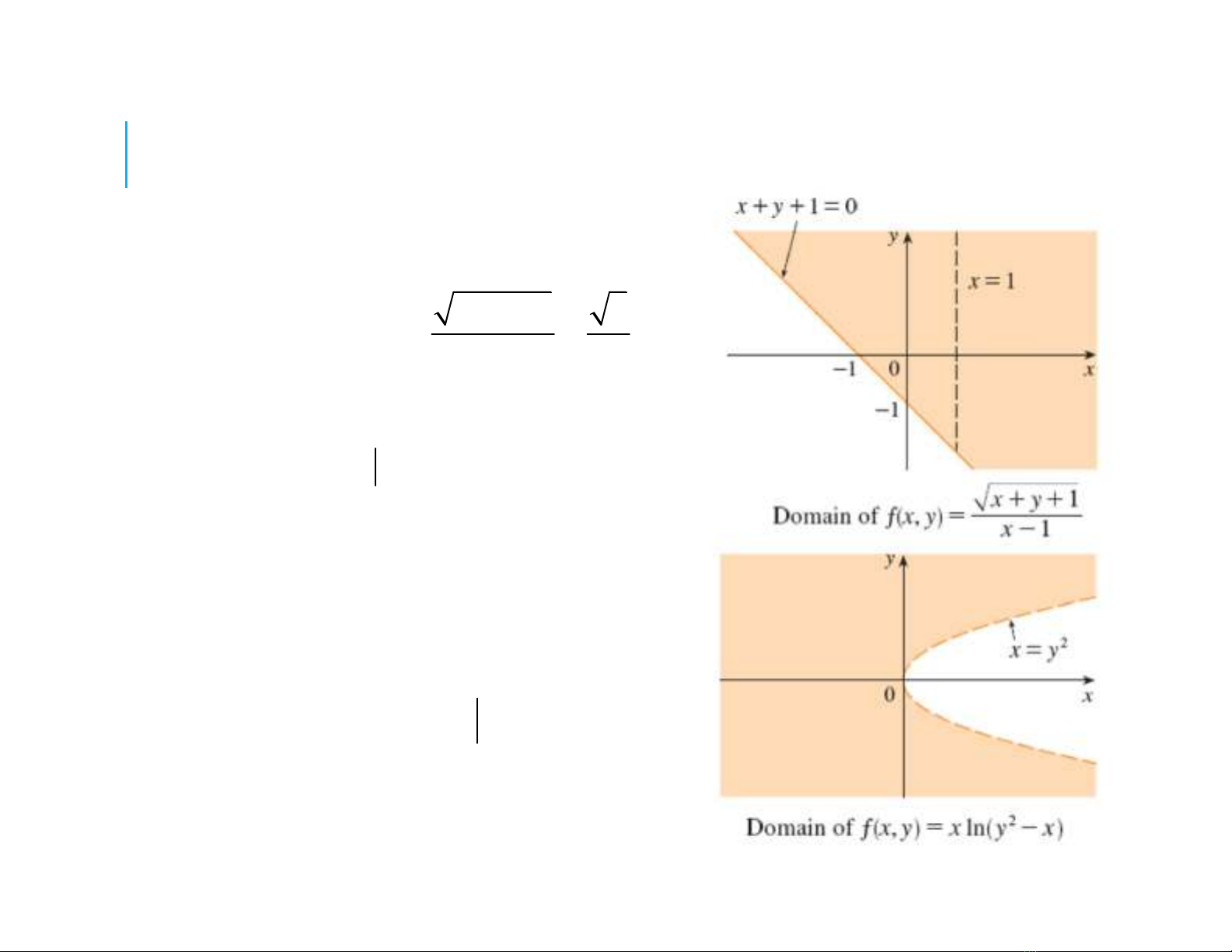
Ví dụ 2. Với mỗi hàm số sau, tìm f(3,2) và miền xác định.
a)
1
,
1
x y
f x y
x
b)
2
, ln
f x y x y x
TẬP XÁC ĐỊNH HÀM HAI BIẾN
A) Ta có:
Tập xác định:
b) Ta có:
Tập xác định:
3 2 1 6
3,2
3 1 2
f
, 1 0, 1
D x y x y x
2
3,2 3ln 2 3 0
f
2
,
D x y x y