TRƯỜNG ĐẠI HỌC SƯ PHẠM HUẾ
KHOA TOÁN
BÀI TẬP NHÓM
MÔN
ĐÁNH GIÁ DẠY HỌC TOÁN
ĐỀ TÀI
CÁC MỨC ĐỘ NHẬN THỨC THEO
BLOOM TRONG CHỦ ĐỀ GIỚI HẠN
NGUYỄN NGỌC THẮNG
HOÀNG CƯỜNG
NGUYỄN THỊ TUYẾT NHUNG
LÊ VĂN MINH TUẤN
NHÓM 7, TOÁN 4B, KHÓA 2007-2011
HUẾ - 11/2010
CÁC MỨC ĐỘ NHẬN THỨC THEO BLOOM
TRONG CHỦ ĐỀ GIỚI HẠN
Nhóm 7, Lớp Toán 4B
1 Nhận biết
1.1 Kiến thức và thông tin về giới hạn
•Trong phạm trù này, học sinh được đòi hỏi gợi ra định nghĩa, ký hiệu khái
niệm của một sự kiện và chưa cần phải hiểu. Những câu hỏi đưa ra trong
mục này kiến thức học sinh đã được học.
•Những phạm trù chính của kiến thức:
–Kiến thức về thuật ngữ: Học sinh được yêu cầu phải nhận diện và làm
quen với ngôn ngữ toán học.
Ví dụ: Cho dãy số (un):un=sin n
n+ 5. Chứng minh rằng: un→0khi
n→+∞. Học sinh cần phải nhận ra đây là một bài toán tìm giới hạn
của dãy số.
–Kiến thức về những sự kiện cụ thể: Mục tiêu này đòi hỏi học sinh gợi
ra được công thức và những mối quan hệ.
Ví dụ: Khả năng nhớ lại các quy tắc tìm giới hạn ở vô cực khi gặp
những bài toán như: Tìm các giới hạn sau
a) lim
n→+∞n(1 −n2); b) lim
n→+∞(3n2−101n−51);
c) lim
n→+∞−5
3n2−101n−51;d) lim
n→+∞
3n3+ 2n−1
2n2−n.
Như vậy học sinh giải quyết được 3 bài toán trên thì trước hết học sinh
cần ghi nhớ lại 3 quy tắc tìm giới hạn ở vô cực:
–Kiến thức về cách thức và phương tiện sử dụng trong trường hợp cụ
thể.
Ví dụ: Trong giới hạn thì sử dụng nhiều kí hiệu. Ví dụ: lim
n→+∞un;un→0
khi n→+∞;lim
x→x0
−
f(x) = L;lim
x→x0+f(x) = L.
–Kiến thức về các quy tắc và tổng quát hóa: Điều này đòi hỏi học sinh
gợi ra được các trừu tượng của toán học để mô tả. Kiến thức này chủ
yếu nằm ở phần định lý và những quy tắc toán học.
•Học xong phần giới hạn học sinh có thể:
–Phát biểu định nghĩa, định lý, quy tắc tìm giới hạn.
1
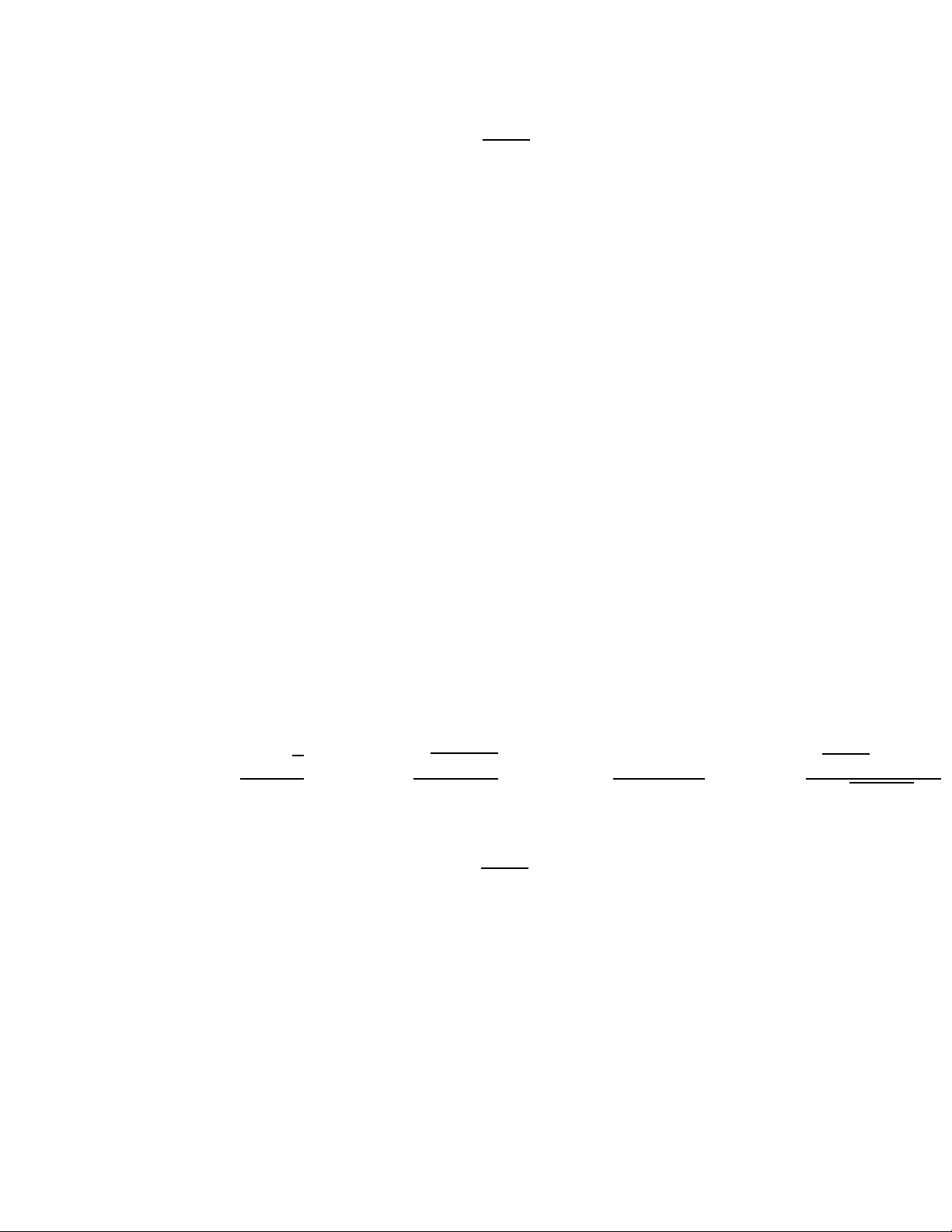
–Cách chứng minh một hàm số liên tục trên trên miền xác định khi cho
hàm số xác định bởi nhiều công thức.
Ví dụ: Chứng minh hàm số sau liên tục trên R
f(x) = (x2−3x+ 2 với x < 2
√x−2với x≥2.
Tìm lim
x→2−
f(x),lim
x→2+f(x),lim
x→2f(x).
1.2 Những kỹ thuật và kỹ năng
•Sử dụng các thuật toán như các kỹ năng thao tác và khả năng thực hiện
trực tiếp các phép tính.
•Câu hỏi có thể không đòi hỏi phải đưa ra quyết định làm thế nào để tiếp
cận bài toán, chỉ cần dùng các kỹ thuật đã được học, hoặc có thể là một
quy tắc phải được nhắc lại mà áp dụng thẳng kỹ thuật đã được học.
•Sau khi học giới hạn học sinh nắm các kỹ thuật:
–Biết cách khử các dạng vô định.
–Tính được các giới hạn của dãy có giới hạn hữu hạn, vô cực.
–Tính được các giới hạn của hàm số tại một điểm, giới hạn một bên.
–Biết cách chứng minh hàm số liên tục trên một miền xác định nếu hàm
số cho bởi nhiều công thức trên từng khoảng, đoạn.
•Một số ví dụ:
Câu 1: Tìm giới hạn
a) lim
x→9
3−√x
9−x;b) lim
n→+∞
√2n4−n
1−3n2;c) lim
x→−1
x2−x−2
x3+x2;d) lim
x→1−
√1−x+x−1
√x2−x3
Câu 2: Chứng minh hàm số sau liên tục trên R
f(x) = (√x−2với x≥2
x−2với x < 2.
2 Thông hiểu
Là khả năng học sinh nắm bắt được ý nghĩa của các vấn đề về giới hạn trong đó
bao gồm các quá trình: Chuyển đổi, giải thích và ngoại suy. Ví dụ như chuyển đổi
các kiến thức từ dạng này sang dạng khác, từ mức độ trừu tượng này sang mức
độ trừu tượng khác. Giải thích, suy ra ý nghĩa của các vấn đề về giới hạn của dãy
số, của hàm số. Mở rộng các lập luận và giải các bài toán về giới hạn. Phạm trù
2
này gồm những câu hỏi để học sinh có thể áp dụng các kiến thức được học về
giới hạn mà không cần liên hệ với các kiến thức khác, hay nhận ra được các vấn
đề ứng dụng của giới hạn, chưa đòi hỏi học sinh phải áp dụng hay phân tích nó.
Phạm trù thông hiểu có thể chia thành 3 loại theo thứ tự: Chuyển đổi, giải thích,
ngoại suy.
2.1 Chuyển đổi
Trong vấn đề giới hạn, quá trình chuyển đổi được thể hiện bằng sự chuyển đổi ý
tưởng thành các dạng song song. Học sinh được yêu cầu thay đổi từ dạng ngôn
ngữ này sang dạng ngôn ngữ khác.
Các ví dụ thuộc phạm trù chuyển đổi. Cuối học kỳ này, học sinh có khả năng:
•Viết dưới dạng ký hiệu một định nghĩa, mệnh đề,... và ngược lại.
•Biểu thị bằng hình học giới hạn của một dãy số đơn giản.
Ví dụ 2.1. Định nghĩa về giới hạn của hàm số tại vô cực.
Giả sử hàm số fxác định trên (a; +∞). Ta nói rằng hàm số fcó giới hạn là số
thực Lkhi xdần đến +∞nếu với mọi dãy số (xn)trong khoảng (a; +∞)(tức là
xn> a với mọi n) mà lim xn= +∞ta đều có lim f(xn) = L.
Phân tích. Học sinh đọc định nghĩa trên, có thể dựa vào từng ký hiệu để diễn
đạt lại như sau:
lim
x→+∞f(x) = L⇔ ∀(xn)n⊂(a, +∞),lim
n→+∞xn= +∞ ⇒ lim
n→+∞f(xn) = L.
Ví dụ 2.2. Biểu diễn hình học giới hạn limn→∞
1
2n= 0.
Phân tích. Trước hết học sinh sẽ liệt kê một số phần tử của dãy un=1
2n.
1
2,1
22,1
23,1
24, ...
Tìm cách thể hiện mối quan hệ của các phần tử trên bằng hình vẽ. Có nhiều cách
thể hiện, học sinh có thể chọn cách sau:
1/2 y
x
b
b
b
E
b
F
b
G
b
H
b
I
b
J
3
2.2 Giải thích
Học sinh phải xác định và hiểu các ý tưởng được trình bày và các mối quan hệ
của các dữ kiện trong vấn đề giới hạn. Từ việc phán xét các dữ kiện quan trọng,
học sinh sẽ tổ chức lại các kiến thức thành một tổng thể để nhận ra được nội
dung của vấn đề.
Ví dụ trong phạm vi giải thích, cuối kỳ học này học sinh có khả năng:
•Đánh giá tính đúng sai của các bài toán tìm giới hạn.
•Từ biểu diễn hình học, đồ thị có thể suy ra được giới hạn của một hàm số.
•Từ một số sơ đồ, hình vẽ, chỉ ra được giới hạn của dãy số nào.
Ví dụ 2.3. Tìm giới hạn lim
x→0
1
x.
a) +∞; b) −∞; c) 0; d) Không có giới hạn.
Phân tích. Gặp bài toán này, học sinh lúc đầu sẽ cho rằng lim
x→0
1
x=∞. Nhưng
sẽ không biết giới hạn đó bằng +∞hay −∞ (theo các đánh giá đưa ra). Từ đó
học sinh sẽ suy nghĩ và tìm lim
x→0+
1
x= +∞,lim
x→0−
1
x=−∞.
Hàm số trên có giới hạn phải và giới hạn trái khác nhau nên giới hạn trên không
tồn tại.
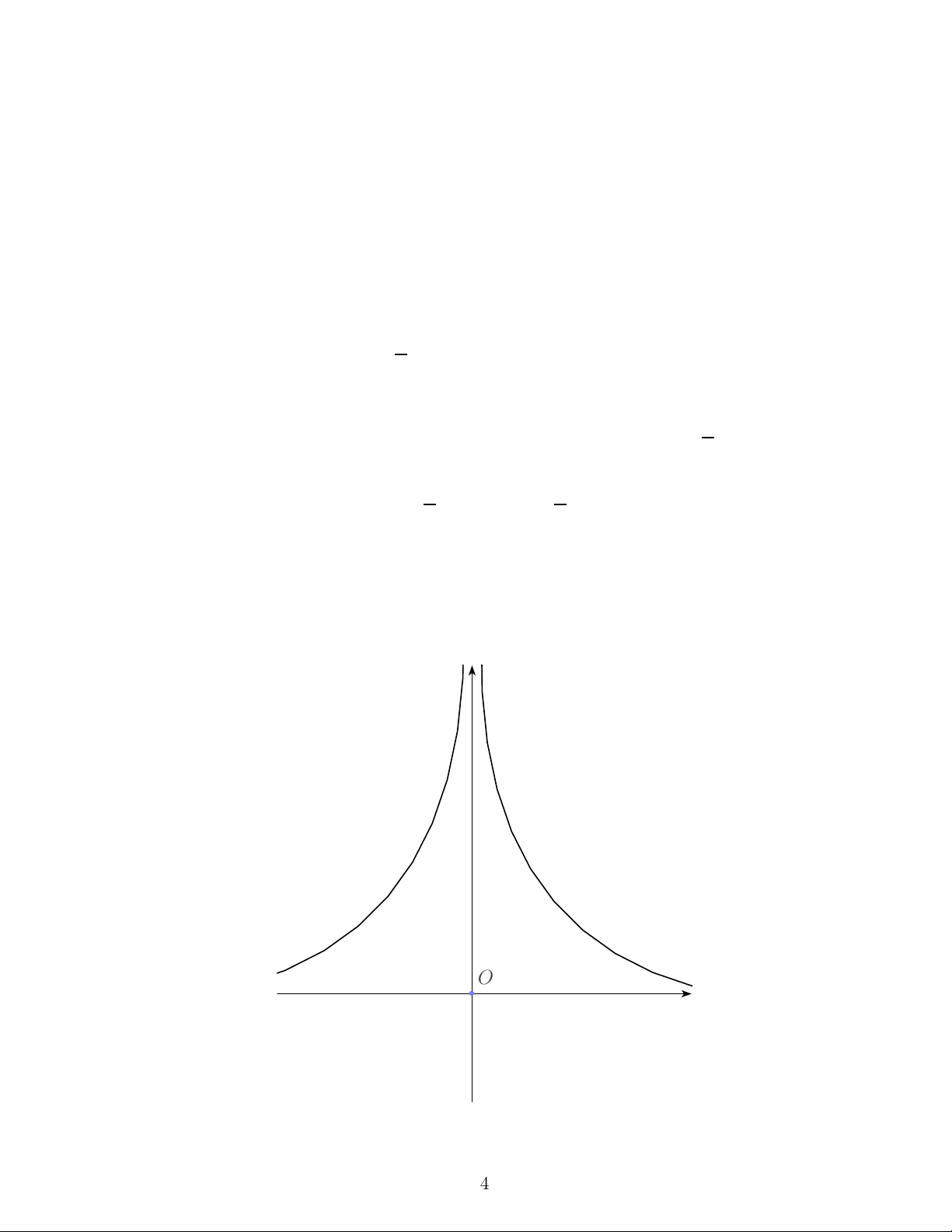
Ví dụ 2.4. Cho đồ thị hàm số sau, nhận xét nào dưới đây là đúng?
bb
O
b
bb
4