BÀI T P LO I 1Ậ Ạ
BÀI T P LO I 1Ậ Ạ
1. V t t c ẽ ấ ả đ thồ ị
a. 3 đnh và 3 c nh.ỉ ạ
b. 4 đnh, 4 c nh và không có vòng, không có c nh //.ỉ ạ ạ
c. li t kê 4 ệđ th ồ ị đu trong 2 trề ư ng h p trên.ờ ợ
d. đu, 4 ềđnh, m i ỉ ỗ đnh b c 3, không vòng, không có ỉ ậ
c nh //.ạ
e. đu, 5 ềđnh, m i ỉ ỗ đnh b c 3.ỉ ậ
2. T i m t câu l c b có 9 thành viên ng i ạ ộ ạ ộ ồ ăn v i nhau m i ớ ỗ
ngày m t bàn tròn, m i ngở ộ ỗ ư i mu n m i ngày 2 ngờ ố ỗ ư i b n ờ ạ
k bên là b n m i. S x p x p kéo dài trong bao nhiêu ngày ?ế ạ ớ ự ắ ế
INSTANT INSANITY
INSTANT INSANITY
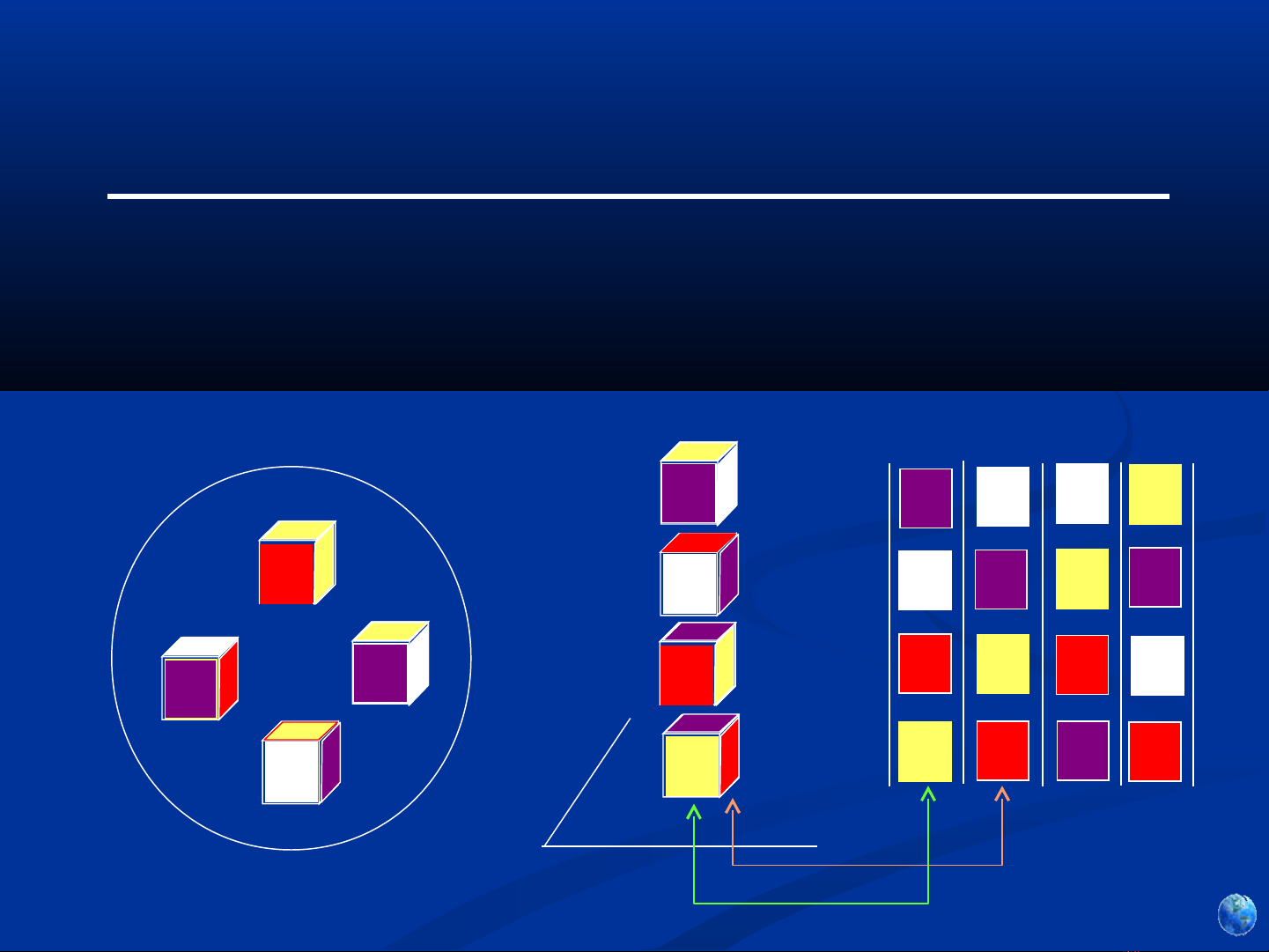
3. Cho 4 kh i vuông, 6 m t c a m i kh i vuông ố ặ ủ ỗ ố đưc tô b ng 4 ợ ằ
màu khác nhau. Có th x p x p 4 kh i thành m t c t sao cho ể ắ ế ố ộ ộ
m i m t c a c t có 4 màu khác nhau ?.ỗ ặ ủ ộ
BÀI T PẬ
BÀI T PẬ
4. M t ộđ th có 21 c nh có 7 ồ ị ạ đnh b c 1, 3 ỉ ậ đnh b c 2, 7 ỉ ậ đnh ỉ
b c 3, các ậđnh còn l i b c 4. Đ th có bao nhiêu ỉ ạ ậ ồ ị đnh ?. N u ỉ ế
thêm 6 đnh b c 0 thì câu tr l i là bao nhiêu.ỉ ậ ả ờ
5. Ch ng minh trong ứđ th ồ ị đơn gi n có ít nh t 2 ả ấ đnh thì ph i ỉ ả
có ít nh t 2 ấđnh có cùng b c.ỉ ậ
6. Các đ th sau có bao nhiêu ồ ị đnh n u chúng có :ỉ ế
a. 12 c nh, t t c ạ ấ ả đnh b c 2.ỉ ậ
b. 15 c nh, 3 ạđnh b c 4, các ỉ ậ đnh còn l i b c 3.ỉ ạ ậ
c. 20 c nh, các ạđnh có cùng b c.ỉ ậ
BÀI T PẬ
BÀI T PẬ
7. S ốđnh l n nh t trong m t ỉ ớ ấ ộ đ th 19 c nh và các ồ ị ạ đnh có b c ỉ ậ
ít nh t là 3 là bao nhiêu ?.ấ
8. Ch ng minh ứđ th ồ ị đơn gi n v ảđnh có s c nh t i ỉ ố ạ ố đa
v(v1)/2.
9. N u ếđ th ồ ị đơn gi n có 50 c nh, s ả ạ ố đnh nh nh t là bao ỉ ỏ ấ
nhiêu?. T ng quát cho n c nh.ổ ạ
10. Ch ng minh m t ứ ộ đ th ồ ị đu b c l ph i có s ề ậ ẻ ả ố đnh ch n.ỉ ẵ
BÀI T PẬ
BÀI T PẬ
11. Đ th <g> có v ồ ị đnh, t t c các ỉ ấ ả đnh có b c l ngo i tr ỉ ậ ẻ ạ ừ
m t ộđnh. Có bao nhiêu ỉđnh b c l trong ỉ ậ ẻ đ th bù c a <g> ?.ồ ị ủ
12. G i e là s c nh, v là s ọ ố ạ ố đnh c a ỉ ủ đ th , t(i) là s ồ ị ố đnh b c ỉ ậ
i. ch ng minh 2e ứ v = t(0) + t(2) + 2t(3) +...+ (k1)t(k).