LÝ THUY T Đ THẾ Ồ Ị
ntsonptnk@gmail.com
N I DUNGỘ
1. Đ i c ng v đ thạ ươ ề ồ ị
2. Cây
3. Các bài toán đ ng điườ
4. Đ th ph ng và bài toán tô màu đ thồ ị ẳ ồ ị
5. M ng và bài toán lu ng trên m ng, bài toán ạ ồ ạ
c p ghépặ
GV: Döông Anh Ñöùc 2
TÀI LI U THAM KH OỆ Ả
1. Giáo trình Lý Thuy t Đ Th - ế ồ ị D ng Anh Đ c, ươ ứ
Tr n Đan Thầ ư
2. Toán r i r c – ờ ạ Nguy n Tô Thành, Nguy n Đ c ễ ễ ứ
Nghĩa
3. ...
GV: Döông Anh Ñöùc 3
Đ I C NG V Đ TH Ạ ƯƠ Ề Ồ Ị
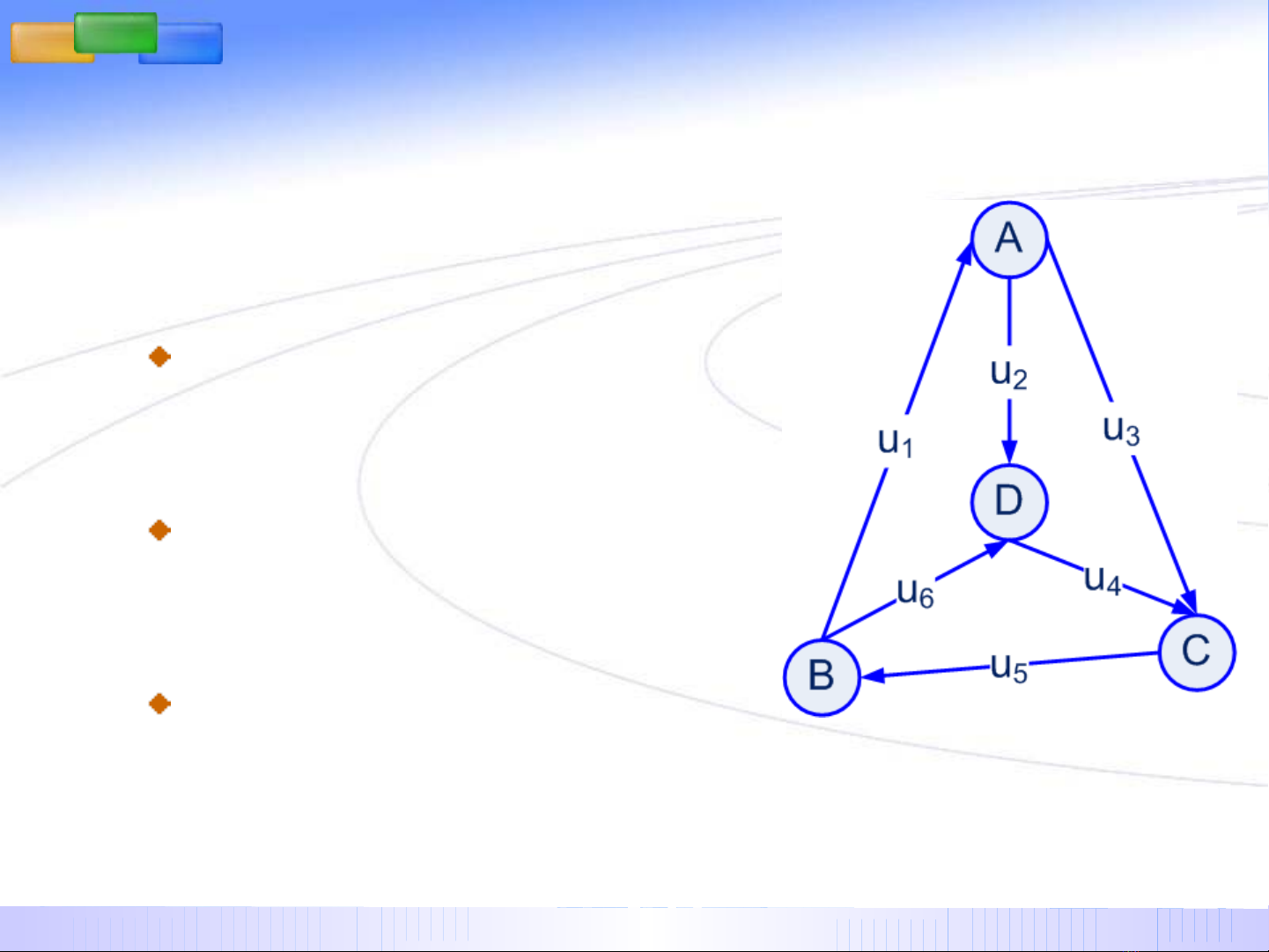
Đ NH NGHĨAỊ
M t đ th có h ng G=(X, ộ ồ ị ướ
U) đ c đ nh nghĩa b i:ượ ị ở
T p h p X ậ ợ ≠ ∅ đ c g i là ượ ọ
t p các đ nh c a đ th ;ậ ỉ ủ ồ ị
T p h p U là t p các c nh ậ ợ ậ ạ
c a đ th ;ủ ồ ị
M i c nh uỗ ạ ∈U đ c liên k t ượ ế
v i m t c p đ nh (i, j)ớ ộ ặ ỉ ∈X2.
GV: Döông Anh Ñöùc 5