ĐẠI HỌC QUỐC GIA THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG ĐẠI HỌC BÁCH KHOA
NĂM HỌC 2021 - 2022
-------*-------
BÀI TẬP LỚN
Môn: Phương pháp tính
Đề: Project 3
GVHD: Đậu Thế Phiệt
Nhóm: 03---HK 211
Họ và tên MSSV Nhiệm vụ
Lê Xuân Thiên 2014566 Problem 1
Võ Hữu Thịnh 2014610 Problem 3
Nguyễn Thanh Ngân 1813206 Problem 3
Hồ Minh Hoàng 1913420 Problem 2
2
Problem 1)
I. Cơ sở lý thuyết
1. Phương pháp chia đôi
–Phương pháp được sử dụng với mục đích tìm nghiệm gần đúng của
phương trình f(x)= 0 với f(x) là hàm liên tục trong miền xác định của nó.
–Phương pháp này chỉ áp dụng với những nghiệm đơn nghĩa là trong 1
khoảng [a;b] chỉ có 1 nghiệm duy nhất và ta sẽ luôn luôn có f(a)*f(b) < 0.
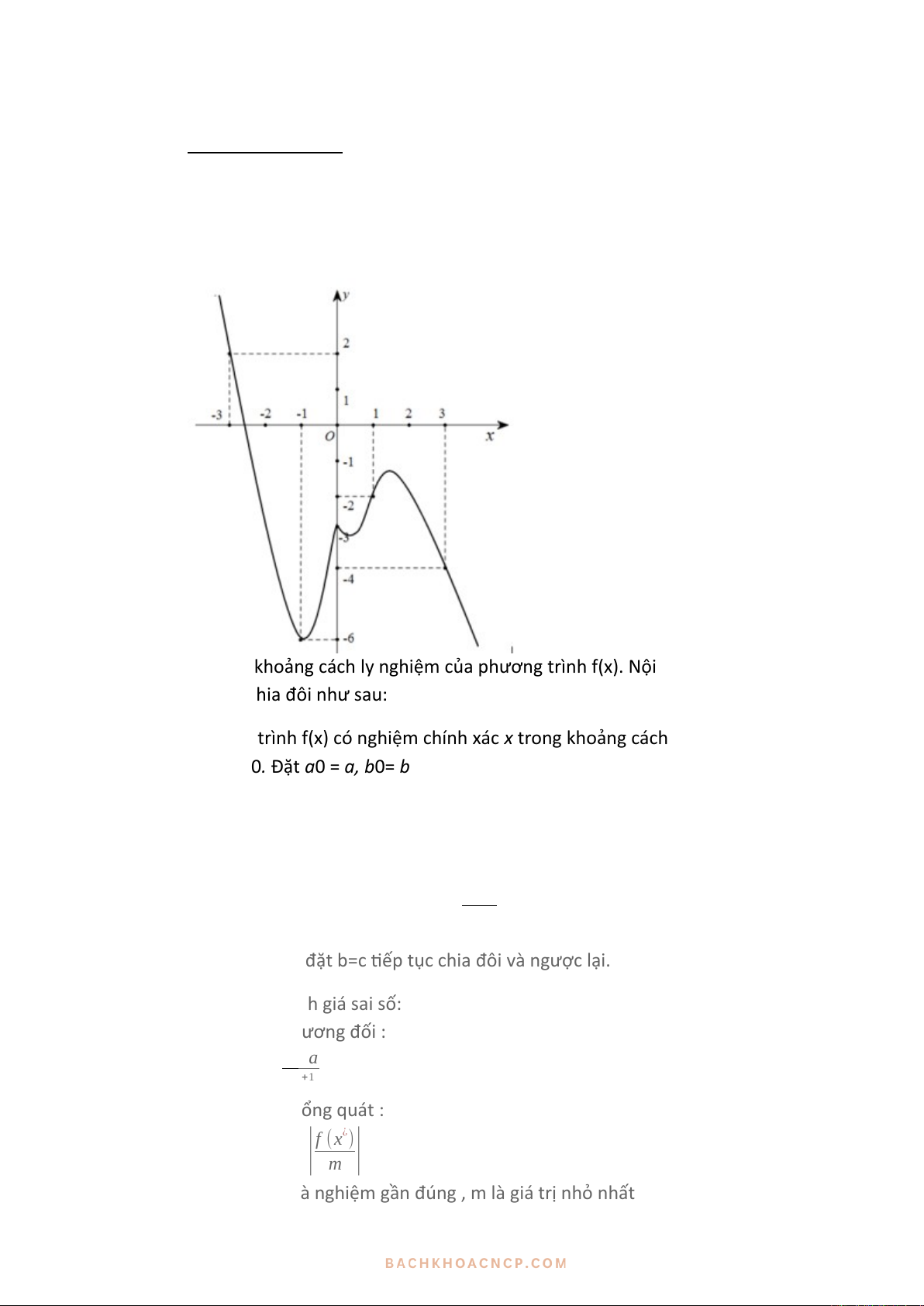
Giả sử (a, b) là khoảng cách ly nghiệm của phương trình f(x). Nội dung của
phương pháp chia đôi như sau:
Giả sử phương trình f(x) có nghiệm chính xác x trong khoảng cách ly nghiệm [a, b]
và f (a)*f (b) < 0. Đặt a0 = a, b0= b
Ta có:
c=a+b
2
Nếu f (a)*f (c) < 0 thì đặt b=c tiếp tục chia đôi và ngược lại.
–Công thức đánh giá sai số:
Sai số tương đối :
∆
x
n
=b−a
2
n+1
Sai số tổng quát :
|
x
¿
−´x
|
=
|
f(x
¿
)
m
|
Với
x
¿
là nghiệm gần đúng , m là giá trị nhỏ nhất
f
'
(x)
trên [a,b]
3
Nhận xét:
Ưu điểm : đơn giản dễ lập trình
Nhược điểm : tốc độ hội tụ chậm độ chính xác không cao.
2. Bài toán Cauchy
Bài toán Cauchy hay còn gọi là bài toán điều kiện ban đầu:
{
y,
(
t
)
=f
(
t , y
(
t
)
)
v iớt ≥ t0
y
(
t0
)
=y0
Với
y=y(t)
là hàm khả vi cần tìm, khả vi với
,
y0
là giá trị ban đầu cho trước
của hàm tại thời điểm
t=t0
và
f(t , y )
là hàm hai biến liên tục cùng với các đạo
hàm riêng của nó.
Đối với bài toán Cauchy ta chỉ có thể tìm được nghiệm đúng của một số phương
trình đơn giản, còn đối với trường hợp f (x, y) có dạng bất kỳ thì nói chung không
có phương pháp giải.
Ngoài ra, trong những trường hợp có thể tìm ra nghiệm đúng của bài toán Cauchy
quá phức tạp thì người ta cũng ít dùng. Vì vậy, việc tìm những phương pháp giải
gần đúng bài toán Cauchy có vai trò rất quan trọng trong thực tế.
a) Phương pháp Euler’s
–Giả sử bài toán Cauchy trên có nghiệm gần đúng trên [a;b] thì ta chia đoạn
[a;b] thành n đoạn nhỏ bằng nhau:
h=b−a
n
–Khi đó
t0=a,tk=t0+kh , v iớk=0,1,2,3 ,.. ,n ,tn=b
–Giả sử
y(t)
là nghiệm duy nhất của bài toán và có đạo hàm liên tục trên
đoạn [a;b] thì ta luôn có trên đoạn [
tk;tk+1¿∈
[
a ; b
]
với k=0,1,2,…,n-1 :
y
(
t
k+1
)
=y
(
t
k
)
+y
,
(
t
k
) (
t
k+1
−t
k
)
+y
,,
(ε
k
)(t
k+1
−t
k
)
2
2
Với
εk∈
(
tk; tk+1
)
–
h=
(
tk+1−tk
)
nên ta có :
y
(
t
k+1
)
=y
(
t
k
)
+y
,
(
t
k
)
∗h+y
, ,
(ε
k
)h
2
2
–Bằng cách bỏ đi phần dư ta được:
y
(
tk+1
)
≈ y
(
tk
)
+h∗f(tk; yk)
Và đây chính là công thức Euler’s
b) Công thức Rungge-Kutta’s
4
–Công thức Runge-Kutta có độ chính xác cao hơn công thức Euler, vì dùng
khai triển Taylor nghiệm y =y(x) của bài toán (1) với nhiều số hạng hơn.
Sử dụng quá trình xây dựng trên đối với công thức Taylor bâc cao hơn, ta
có thể xây dựng Phương pháp Runge - Kutta với các bậc cao, và phổ biến
nhất là bậc 4
{
K
1
=hf (t
k
; y
k
)
K
2
=hf (t
k
+h
2; y
k
+K
1
2)
K
3
=hf (t
k
+h
2; y
k
+K
2
2)
K
4
=hf (t
k
+h ; y
k
+K
3
)
y
k+1
=y
(
t
k
+h
)
=y
k
+1
6(K
1
+2K
2
+2K
3
+K
4
)
II. Bài tập vận dụng
A bungee jumper jumps from a mountain with the downward vertical
velocity v described by the mathematical model:
dv
dt =g−C
d
mv
2
(see the picture ) where m is the mass of jumper and cd is called drag
coefficient.
a) Suppose that the jumper is initial at rest, find analytically
the expression of v.
b) Let g = 9.8(m/s2), m = 68.1(kg), cd = 0.25(kg/m) and the
jumper is initial at rest, establish the table to compute the
velocity of the jumper for the first 10 seconds with step size
5