TRƯỜNG ĐẠI HỌC SƯ PHẠM HUẾ
KHOA TOÁN
--------
TỪ CÂU HỎI TRUYỀN THỐNG ĐẾN
CÂU HỎI TRẮC NGHIỆM KHÁCH QUAN
CHỦ ĐỀ:
NGUYÊN HÀM – TÍCH PHÂN VÀ ỨNG DỤNG
Sinh viên: Hoàng Lê Thu Hằng
Lớp: Toán 4T
Mã sinh viên: 13S1011044
Giáo viên hướng dẫn: Thầy Nguyễn Đăng Minh Phúc
Huế, tháng 4 năm 2017.
Sinh viên: Hoàng Lê Thu Hằng Lớp: Toán 4T
- 1 -
Chủ đề: Nguyên hàm – Tích phân và ứng dụng
Bài toán 1: Tính tích phân sau:
𝑰=∫𝒙𝐥𝐧𝒙
(𝒙𝟐+𝟏)𝟐𝒅𝒙
𝟑
𝟏.
Bài giải:
Đặt {𝑢=ln𝑥
𝑑𝑣=𝑥
(𝑥2+1)2𝑑𝑥 ⇒
{
𝑑𝑢=𝑑𝑥
𝑥
𝑣=− 1
2(𝑥2+1)
Áp dụng công thức tích phân từng phần, ta có:
𝐼=− ln𝑥
2(𝑥2+1)|1
3+∫1
2𝑥(𝑥2+1)𝑑𝑥
3
1
=−ln3
20+1
2∫1
𝑥(𝑥2+1)𝑑𝑥
3
1
=−ln3
20+1
2∫ (1
𝑥−𝑥
𝑥2+1)𝑑𝑥
3
1
=−ln3
20+1
2(ln𝑥−1
2ln(𝑥2+1))|1
3
=−ln3
20+1
2(ln3−1
2ln10+1
2ln2)
=9
20ln3−1
4ln5
Vậy 𝐼= 9
20ln3−1
4ln5.
Phân tích:
Để tính được tích phân này, học sinh cần phải hiểu được phương pháp tính tích phân từng
phần, phương pháp đổi biến số để tìm được các nguyên hàm tương ứng, học sinh phải có đầy đủ
các kiến thức cơ bản về phép tính đạo hàm của các hàm cơ bản, phép tính đạo hàm đối với hàm
hợp.
Ngay từ đầu, các em phải xác định được phương pháp tính tích phân nào sẽ được sử dụng
trong bài toán này. Sau khi xác định được phương pháp làm (phương pháp tích phân từng phần),
Sinh viên: Hoàng Lê Thu Hằng Lớp: Toán 4T
- 2 -
học sinh cần phải hiểu được lượng nào sẽ đặt làm 𝑢 và lượng nào đặt làm 𝑑𝑣 để tìm nguyên
hàm. Sau đó, bằng những kỹ năng tính toán của bản thân, các em sẽ thu được kết quả.
Câu hỏi trắc nghiệm:
Câu 1:
Tính 𝐼=∫𝑃(𝑥)ln𝑥𝑑𝑥
𝑏
𝑎 (𝑎,𝑏 ∈ℝ), trong đó 𝑃(𝑥) là đa thức, bằng phương pháp
tích phân từng phần.
A. Đặt {𝑢=𝑃(𝑥)
𝑑𝑣=ln𝑥𝑑𝑥⟹{𝑑𝑢=𝑃′(𝑥)𝑑𝑥
𝑣=1
𝑥 ⟹𝐼=𝑃(𝑥)
𝑥|𝑎
𝑏−∫𝑃′(𝑥)
𝑥
𝑏
𝑎𝑑𝑥.
B. Đặt {𝑢=𝑃(𝑥)
𝑑𝑣=ln𝑥𝑑𝑥⟹{𝑑𝑢=𝑃′(𝑥)𝑑𝑥
𝑣=1
𝑥 ⟹𝐼=𝑃(𝑥)
𝑥|𝑃(𝑎)
𝑃(𝑏)−∫𝑃′(𝑥)
𝑥
𝑃(𝑏)
𝑃(𝑎) 𝑑𝑥.
C. Đặt {𝑢=ln𝑥
𝑑𝑣=𝑃(𝑥)𝑑𝑥⟹{𝑑𝑢=1
𝑥𝑑𝑥
𝑣=∫𝑃(𝑥)𝑑𝑥=𝑄(𝑥)⟹𝐼=ln𝑥.𝑄(𝑥)|𝑎
𝑏−∫𝑄(𝑥)
𝑥
𝑏
𝑎𝑑𝑥.
D. Đặt {𝑢=ln𝑥
𝑑𝑣=𝑃(𝑥)𝑑𝑥⟹{𝑑𝑢=1
𝑥𝑑𝑥
𝑣=∫𝑃(𝑥)𝑑𝑥=𝑄(𝑥)⟹𝐼=ln𝑥.𝑄(𝑥)|𝑒𝑎
𝑒𝑏−∫𝑄(𝑥)
𝑥
𝑒𝑏
𝑒𝑎𝑑𝑥.
Đáp án: C.
Học sinh thường gặp sai lầm khi làm các bài toán tích phân liên quan đến hàm 𝑦=ln𝑥, các
em bị nhẫm lẫn giữa đạo hàm và nguyên hàm dẫn đến việc đặt sai các lượng 𝑢 và 𝑑𝑣 (phương
án nhiễu A, B).
Ngoài ra, một số học sinh mắc sai lầm trong việc chọn cận, các em nghĩ rằng ở phương pháp
tích phân từng phần ta cũng phải đổi cận như ở phương pháp đổi biến số dẫn đến việc đưa ra kết
quả sai (phương án nhiễu B, D).
Câu 2:
Tìm nguyên hàm 𝐹(𝑥)=∫𝑥
(𝑥2+1)2𝑑𝑥.
A.𝐹(𝑥)=1
𝑥2+1+𝑐,𝑐∈ℝ.
B.𝐹(𝑥)=− 1
𝑥2+1+𝑐,𝑐∈ℝ.
C.𝐹(𝑥)=1
2(𝑥2+1)+𝑐,𝑐∈ℝ.
D.𝐹(𝑥)=− 1
2(𝑥2+1)+𝑐,𝑐∈ℝ.
Sinh viên: Hoàng Lê Thu Hằng Lớp: Toán 4T
- 3 -
Đáp án: D.
Để tìm nguyên hàm này, học sinh sẽ dử dụng phương pháp đổi biến số, đặt 𝑡=𝑥2+1. Và
ở đây, học sinh thường mắc phải các sai lầm về kỹ năng đạo hàm, kỹ năng tìm nguyên hàm các
hàm cơ bản dẫn đến sai sót (phương án nhiễu A, B, C).
Câu 3:
Bước 1:
1
𝑥(𝑥2+1)=1
𝑥−𝑥
𝑥2+1.
Bước 2:
𝐼=∫ (1
𝑥−𝑥
𝑥2+1)𝑑𝑥
3
1=(ln𝑥−ln(𝑥2+1))|1
3=ln 𝑥
𝑥2+1|1
3.
Bước 3:
𝐼=ln3
10−ln1
2=ln3−ln5.
A. Sai từ Bước 1. B. Sai từ Bước 2. C. Sai từ Bước 3. D. Đúng.
Đáp án: B
Học sinh thường thiếu giá trị 1
2 khi tìm nguyên hàm của hàm số 𝑓(𝑥)=𝑥
𝑥2+1 dẫn đến
sai sót trong quá trình làm bài (phương án nhiễu D).
Bài toán 2:
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 𝒚=|𝒙𝟐−𝟒𝒙+𝟑|
và đường thẳng 𝒅:𝒚=𝒙+𝟑.
Bài giải:
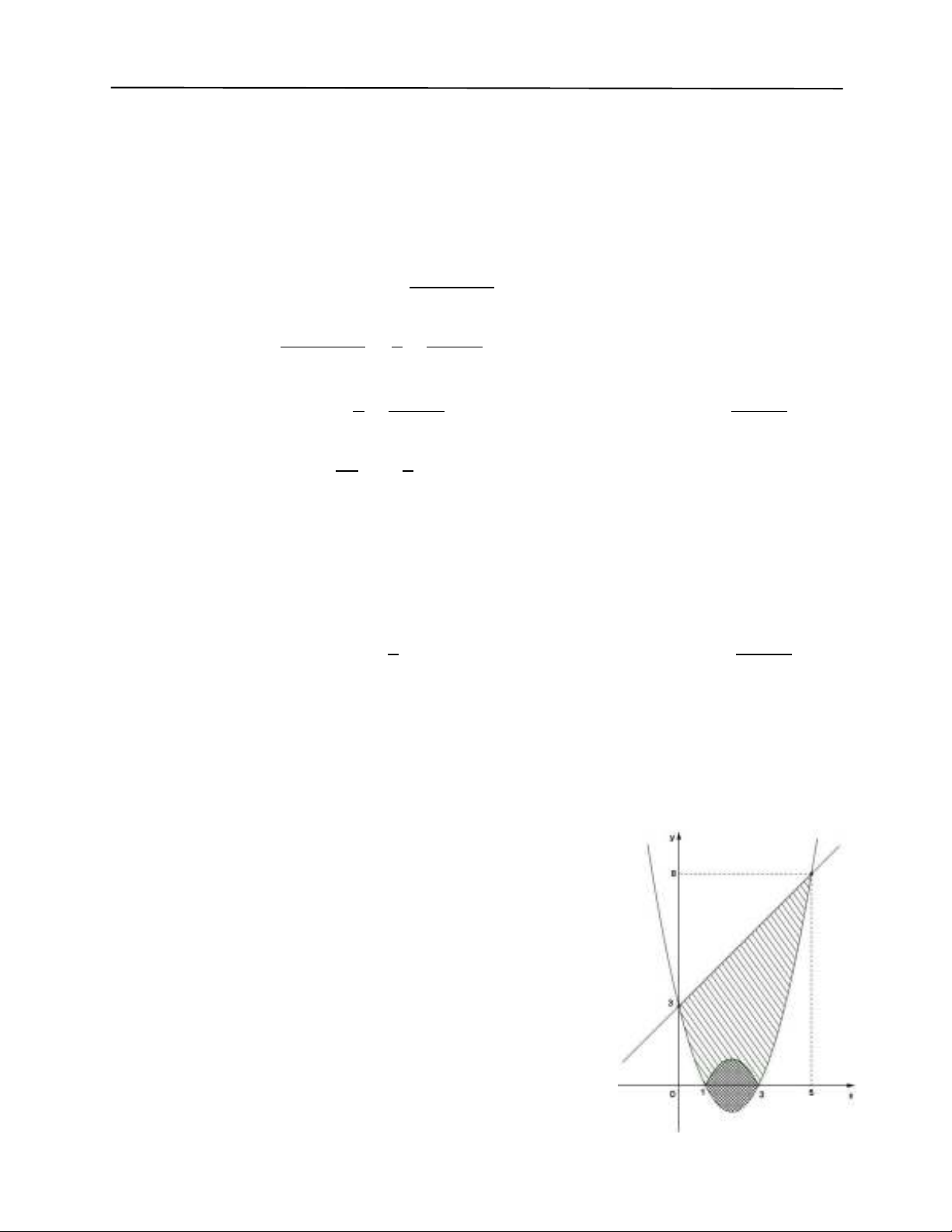
Gọi 𝑆 là phần diện tích hình phẳng giới hạn bởi đồ thị hàm số
𝑦=|𝑥2−4𝑥+3| và đường thẳng 𝑑:𝑦=𝑥+3.
Gọi 𝑆1 và 𝑆2 lần lượt là phần diện tích hình phẳng giới hạn
bởi đồ thị hàm số 𝑦=𝑥2−4𝑥+3 với đường thẳng 𝑑:𝑦=
𝑥+3 và trục hoành.
Suy ra: 𝑆=𝑆1−2𝑆2.
Ta có:
Sinh viên: Hoàng Lê Thu Hằng Lớp: Toán 4T
- 4 -
𝑥2−4𝑥+3=𝑥+3⟺𝑥2−5𝑥=0⟺[𝑥=0
𝑥=5.
Suy ra: 𝑆1=∫|(𝑥2−4𝑥+3)−(𝑥+3)|𝑑𝑥
5
0
=∫|𝑥2−5𝑥|𝑑𝑥
5
0
=∫(5𝑥−𝑥2)𝑑𝑥
5
0
=(5𝑥2
2−𝑥3
3)|0
5
=125
6.
𝑥2−4𝑥+3=0⇔[𝑥=1
𝑥=3.
Suy ra: 𝑆2=∫|𝑥2−4𝑥+3|𝑑𝑥
3
1
=∫(−𝑥2+4𝑥−3)
3
1𝑑𝑥
=(−𝑥3
3+2𝑥2−3𝑥)|1
3
=0−(−4
3)=4
3.
Vậy: 𝑆=𝑆1−2𝑆2=125
6−2.4
3=109
6 (đvdt).
Phân tích:
Để tính được diện tích phần hình phẳng giới hạn bởi đồ thị hàm số 𝑦=|𝑥3−4𝑥+3| và
đường thẳng 𝑑:𝑦=𝑥−3, ta cần xác định được phần hình phẳng đó trên mặt phẳng tọa độ. Do
đó, việc vẽ được đồ thị hai hàm số này đóng vai trò quan trọng trong việc định hướng giải quyết
bài toán.
Sau khi xác định được phần hình phẳng cần tính diện tích, học sinh cần phải có khả năng
quan sát, tư duy, suy luận để tìm được cách tính sao cho hợp lý, dễ dàng và thuận tiện.