Ly thuyêt Qui hoach tuyên tinh
CH NG II: C S QUI HO CH L IƯƠ Ơ Ở Ạ Ồ
§ 1 Bài toán qui ho ch l i c b nạ ồ ơ ả
1.1 Trình bày bài toán qui ho ch l i c b n ạ ồ ơ ả
Cho Γ⊆ Rn, l i, f là hàm l i xác đ nh trên ồ ồ ị Γ, gi, i =1,2,…,m, là m hàm lõm
cũng xác đ nh trên ịΓ, bi , i = 1,2,…,m, là m s th c. D th y r ng, n u t pố ự ễ ấ ằ ế ậ
h pợ
X = {x∈Rn/ gi(x) ≥ bi, i = 1,2,…,m; x∈Γ} (1.1)
không r ng thì nó là t p h p l i, đóng trong Rỗ ậ ợ ồ n (Bài t p 42).ậ
Đ cho g n, ký hi u g(x) = (gể ọ ệ 1(x), g2(x), …, gm(x)) là vect m hàmơ
s , b = (bố1, b2, …, bm) ∈ Rm. Khi đó t p t p X đ c vi t d i d ngậ ậ ượ ế ướ ạ
X = { x∈Rn / g(x) ≥ b, x∈Γ} (1.2)
trong đó ký hi u g(x) ệ≥ b ⇔ gi(x) ≥ bi, i = 1,2, …, m. Bài toán c c tr sauự ị
đây đ c g i là bài toán qui hoach lôi c b n.ượ ọ ơ ả
Tìm x0
∈
X, đ cho ể
0
x X
f (x ) f (x)
min
∈
=
(1.3)
Lý thuy t và các ph ng pháp gi i bài toán (1.3) đ c g i là Lýế ươ ả ượ ọ
thuy t qui ho ch l i. Trong ch ng này ch trình bày ph n lý thuy t làmế ạ ồ ươ ỉ ầ ế
c s cho vi c xây d ng các thu t toán. Các ph ng pháp đ gi i bài toánơ ở ệ ự ậ ươ ể ả
(1.3) s đ c trình bày trong chuyên đ Qui ho ch phi tuy n h c kỳ 7.ẽ ượ ề ạ ế ở ọ
1.2 Đi u ki n chính quiề ệ
Đn 1.1: T p h p X xác đ nh theo (1.1) ho c (1.2) đ c g i là th a ậ ợ ị ặ ượ ọ ỏ mãn
đi u ki n cính quiề ệ , n uế
∀i, 1≤ i ≤ m, ∃ xi: gi(xi) > bi(1.4)
Ngoài ra, t p X cũng đ c coi là tho mãn ậ ượ ả đi u ki n chính quiề ệ
Slater, n u ế
∃ x0: gi(x0) > bi ∀i, 1≤ i ≤ m (1.5)
D th y r ng hai đi u ki n chính qui (1.4) và (1.5) là t ng đ ngễ ấ ằ ề ệ ươ ươ
nhau; t c là n u X th a mãn đi u ki n chính qui (1.4) thì cũng th a đi uứ ế ỏ ề ệ ỏ ề
ki n chính qui (1.5) và ng c l i (Bài t p 43).ệ ượ ạ ậ
Lê Văn Phi, Khoa Toan Thông kê, Tr ng Đai hoc Kinh tê Tp. Hô Chi Minhươ 43
Ly thuyêt Qui hoach tuyên tinh
1.3 Hàm Lagrange
ng v i m i xỨ ớ ọ ∈Γ, xét vect m chi u h(x) = b – g(x), ơ ề
t c là ứ
hi(x) = b – gi(x), i = 1,2,…,m
Trên Γ× {y∈Rm/ y ≥ 0} ta đ nh nghĩa hàm s ị ố
L(x,y) = f(x) + 〈y, h(x)〉 = f(x) +
m
i i i
i 1
y [b g (x)]
=−
∑
(1.6)
Hàm L(x,y) đ c đ nh nghĩa theo (1.6) đ c g i là ượ ị ượ ọ hàm Lagrange ng v iứ ớ
bài toán qui hoach lôi (1.3).
§ 2 Các đi u ki n t i u c a bài toán ề ệ ố ư ủ qui ho
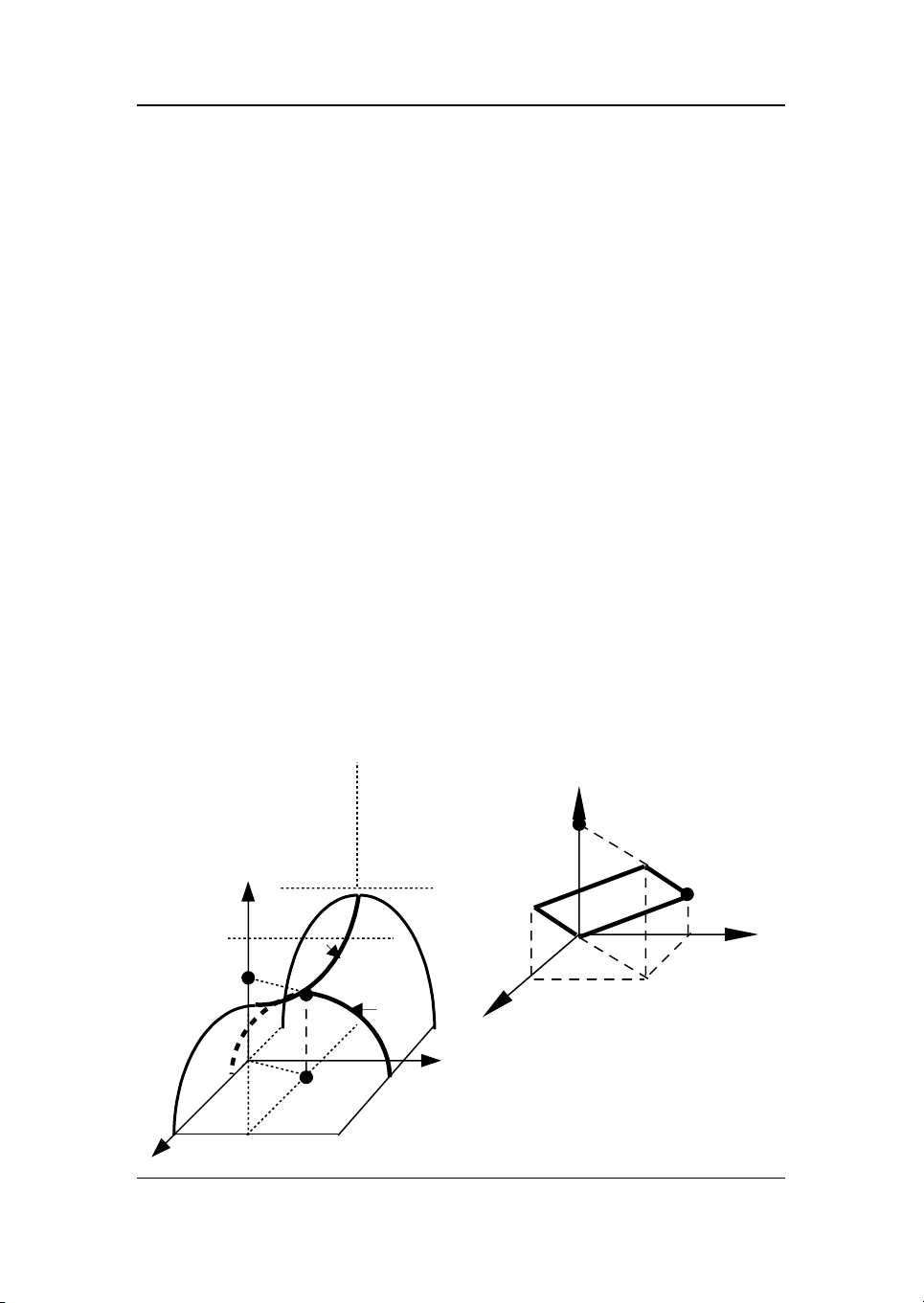
2.1 Đi m yên ng aể ự
Cho S ⊆ Rn, T⊆ Rm và ϕ(s,t) là hàm s xác đ nh trên Số ị ×T.
Đn 2.1: Đi m (s*, t*) ể
∈
S
×
T đ c g i là đi m yên ng a (Hình ) c a hàmượ ọ ể ự ủ
ϕ
(s, t) trên mi n Sề
×
T, n uế
∀s∈S, ∀t∈T : ϕ(s*, t) ≤ ϕ(s*, t*) ≤ ϕ(s, t*)
(2.1)
Hinh 2.1 Hinh 2.2
hình Ở2.1, đi m (s*, t*) = (0; 1) là đi m yên ng a c a hàm ể ể ự ủ ϕ(s,t) = s + t. Vì,
n u gi nguyên t* = 1 và thay đ i s (s ch có th tăng t 0 lên 1) thì giá tr hàm s sế ữ ổ ỉ ể ừ ị ố ẽ
tăng t 1 đ n 2. Trong khi đó, n u gi nguyên s* = 0 và thay đ i t (t ch có th gi mừ ế ế ữ ổ ỉ ể ả
t 1 đ n 0) thì giá tr hàm s gi m t 1 đ n 0. Trong khi đi m (1;0) không ph i làừ ế ị ố ả ừ ế ể ả
đi m yên ng a. ví d này cũng cho th y r ng, đi m yên ng a không ph i là c cể ự Ở ụ ấ ằ ể ự ả ự
Lê Văn Phi, Khoa Toan Thông kê, Tr ng Đai hoc Kinh tê Tp. Hô Chi Minhươ 44
ϕ
ϕ(s, t*)
ϕ(s*, t*)
ϕ(s*, t)
t*
s* t
(s*, t*)
S
S = T = [0;1], ϕ(s, t) = s + t
ϕ
2
(1;1)
(0;1)
(1;0)
1 t
1
s
Ly thuyêt Qui hoach tuyên tinh
tr c a hàm Lagrange. (Giá tr c c ti u c a ị ủ ị ự ể ủ ϕ(s,t) = s + t là 0, t i (0;0), giá tr c c đ iạ ị ự ạ
là 2 t i đi m (1;1).ạ ể
D dàng ch ng minh đ c quan h sau đây:ễ ứ ượ ệ
s S s S
t T t T
(s, t)
sup sup
inf inf
∈ ∈
∈ ∈
φ ≤ φ
(2.2)
Đlí 2.1: Đ cho hàm ể
ϕ
(s,t) có đi m yên ng a trên mi n Sể ự ề
×
T thì đi u ki nề ệ
c n và đ là t n t i các minmax ầ ủ ồ ạ
s St T
(s, t)
maxinf
∈∈
φ
và
s S t T
(s, t)
sup
min
∈∈φ
;
đ ng th i chúng b ng nhauồ ờ ằ .
Ch ng minhứ:
a) Đi u ki n c n: Gi s (s*,t*) là đi m yên ng a c a hàm ề ệ ầ ả ử ể ự ủ ϕ(s,t) trên
mi n Sề×T. Khi đó theo (2.1)
t T
(s*, t) (s*, t*)
sup
∈φ ≤ φ
và do đó
s S t T
(s, t) (s*, t*)
sup
inf
∈∈φ ≤ φ
T ng t ,ươ ự
s S
t T
(s*, t*) (s, t)
supinf
∈
∈
φ ≤ φ
Suy ra b t đ ng th c képấ ẵ ứ
s S s S s S
t T t T t T
(s, t) (s, t*) (s*, t*) (s, t*) (s, t)
sup sup sup
inf inf inf
∈ ∈ ∈
∈ ∈ ∈
φ ≤ φ ≤ φ ≤ φ ≤ φ
T (2.2) suy ra các d u b t đ ng th c bên trong ph i tr thành đ ng th c;ừ ấ ấ ẵ ứ ả ở ẵ ứ
t c là ứ
và
s S s S
t T
(s, t) (s, t*) (s*, t*)
supinf inf
∈ ∈
∈φ = φ = φ
Hay
s St T
(s, t) (s*, t*)
maxinf
∈∈ φ = φ
và
s S t T
(s, t*) (s*, t*)
sup
min
∈∈φ = φ
b) Đi u ki n đ : Gi s các giá tr minmax trong đ nh lý t n t i và b ngề ệ ủ ả ử ị ị ồ ạ ằ
nhau, t c là ứ∃ s*∈S, t*∈T, sao cho
s S s St T
(s, t) (s, t*)
maxinf inf
∈ ∈∈ φ = φ
và
s S t T t T
(s, t*) (s*, t)
sup sup
min
∈∈ ∈
φ = φ
Suy ra
s S t T
(s, t*) (s*, t*) (s*, t)
sup
inf
∈∈
φ ≤ φ ≤ φ
. Theo gi thi t các minmax b ngả ế ằ
nhau, nên các b t đ ng th c ph i tr thành đ ng th c. T c làấ ẵ ứ ả ở ẵ ứ ứ
s S t T
(s, t*) (s*, t*) (s*, t)
sup
inf
∈∈
φ = φ = φ
T đây suy ra ừ∀s∈S, ∀t∈T: ϕ(s*,t) ≤ ϕ(s*,t*) ≤ ϕ(s,t*). T c là c p (s*,t*)ứ ặ
là đi m yên ng a c hàm ể ự ủ ϕ(s,t) trên mi n Sề×T. ª1
1Trong ch ng minh trên các bi n s, t bi n thiên đ c l p, nên n u (s*,t*) và (s’,t’) là nh ngứ ế ế ộ ậ ế ữ
đi m yên ng a c a ể ự ủ ϕ(s,t) thì các c p (s*,t’) và (s’,t*) cũng là đi m yên ng a. ặ ể ự
Lê Văn Phi, Khoa Toan Thông kê, Tr ng Đai hoc Kinh tê Tp. Hô Chi Minhươ 45
Ly thuyêt Qui hoach tuyên tinh
2.2 Đi m yên ng a c a hàm Lagrange L(x,y) và đi u ki n t iể ự ủ ề ệ ố
u ư
Theo ph n 1.3, hàm Lagrange c a bài toán qui hoach lôi c b n (1.3)ầ ủ ơ ả
xác đ nh trên mi n ị ề Γ× {y∈Rm/ y ≥ 0} có d ngạ
L(x,y) = f(x) + 〈y, h(x)〉 = f(x) +
m
i i i
i 1
y [b g (x)]
=−
∑
(1.6)
Theo Đn 2.1, thì c p (ặx*, y*) là đi m yên ng a c a L(ể ự ủ x,y) trên mi nề
Γ× {y∈Rm/ y ≥ 0} khi
∀x∈Γ, ∀y≥ 0: L(x*,y) ≤ L(x*,y*) ≤ L(x,y*) (2.3)
Do L(x,y) l i theo ồx và tuy n tính theo ếy, đ ng th i các t p ồ ờ ậ Γ và {y∈Rm/ y
≥ 0} là nh ng t p đóng, nên ữ ậ Đlí 2.2 tr thành: Đ cho hàm Lagrangeở ể
L(x,y) có đi m yên ng a trên mi n ể ự ề Γ× {y∈Rm/ y ≥ 0} thì đi u ki n c n vàề ệ ầ
đ là các minmax ủ
xy 0
L(x, y)
maxmin
∈Γ≥
x y 0
L(x, y)
max
min
∈Γ ≥
(2.4)
t n t i và b ng nhau.ồ ạ ằ
Quan h gi a đi m yên ng a c a hàm L(ệ ữ ể ự ủ x,y) và l i gi i c a bàiờ ả ủ
toán qui hoach l i c b n (1.3) đ c cho b i đ nh lý sau đây. ồ ơ ả ượ ở ị
Đlí 2.2: N u (ếx*, y*) là đi m yên ng a c a hàm L(ể ự ủ x,y) trên mi nề
Γ×
{y
∈
Rm, y
≥
0} thì x* là l i gi i c a bài toán (1.3).ờ ả ủ
Ch ng minhứ: Gi s (ả ử x*, y*) là đi m yên ng a c a hàm L(ể ự ủ x,y) trên mi nề
Γ× {y∈Rm, y ≥ 0}. T c là ứ∀x∈Γ, ∀ y ≥ 0 :
f(x*) + 〈y, h(x*)〉 ≤ f(x*) + 〈y*, h(x*)〉 ≤ f(x) + 〈y*, h(x)〉 (2.5)
T đây suy ra:ừ
a) ∀ y ≥ 0 : 〈y, h(x*)〉 ≤ 〈y*, h(x*)〉 (2.6)
D th y r ng đi u ày ch xãy ra khi h(ễ ấ ằ ề ỉ x*) ≤ 0. T c là ứb – g(x*) ≤ 0; hay
g(x*) ≥ b. K t h p v i gi thi t ế ợ ớ ả ế x*∈Γ, suy ra x*∈X.
b) Do (2.6) đúng v i m i ớ ọ y ≥ 0 nên cũng đúng khi y = 0. T (2.6) suy raừ
〈y*, h(x*)〉 ≥ 0. M t khác, do h(ặx*) ≤ 0, nên ta cũng có b t đ ng th cấ ẵ ứ
ng c l i. ượ ạ Suy ra 〈y*, h(x*)〉 = 0.
c) T đây và t (2.5) suy ra ừ ừ ∀x∈Γ : f(x*) ≤ f(x) + 〈y*, h(x)〉. Đ c bi t khiặ ệ
x∈X, thì h(x) ≤ 0, nên 〈y*, h(x)〉 ≤ 0. Do đó f(x*) ≤ f(x), ∀x∈X. T cứ
là x* là l i gi i c a bài toán (1.3).ªờ ả ủ
Lê Văn Phi, Khoa Toan Thông kê, Tr ng Đai hoc Kinh tê Tp. Hô Chi Minhươ 46
Ly thuyêt Qui hoach tuyên tinh
Đ nh lý 2.2 cho bi t đi u ki n đ đ m t vect x* là l i gi i c a bài toánị ế ề ệ ủ ể ộ ơ ờ ả ủ
QH l i c b n (1.3). T đ nh lý này suy ra, đ gi i bài toán (1.3) ch c nồ ơ ả ừ ị ể ả ỉ ầ
tìm m t đi m yên ng a c a hàm Lagrange t ng ng L(x,y).ộ ể ự ủ ươ ứ
2.3 Đ nh lý Kuhn- Tuckerị
Đlý 2.3: Gi s r ng t p X th a mãn đi u ki n chính qui. Khi đó đ choả ử ằ ậ ỏ ề ệ ể
đi m ểx*
∈Γ
là l i gi i c a bài toán QH l i c b n (1.3) thì đi uờ ả ủ ồ ơ ả ề
ki n c n và đ là t n t i đi m ệ ầ ủ ồ ạ ể y*
≥
0 đ cho c p (ể ặ x*, y*) là
đi m yên ng a c a hàm Lagrange L(ể ự ủ x,y) trên mi n ề
Γ×
{y
∈
Rm, y
≥
0}.
Ch ng minhứ: Đi u ki n đề ệ ủ suy t đ nh lý 2.2 mà không c n có đi u ki nừ ị ầ ề ệ
chính qui. Ta ch ng minh ứđi u ki n c nề ệ ầ . Gi s ả ử x* là l i gi i c a bài toánờ ả ủ
QH l i c b n (1.3).ồ ơ ả
1) Xét tâp P = {(z0, z) ∈R (m+1)/ z0 ≤ f(x*), z ≤ 0}. V i ớx∈Γ, đ t ặ
S(x) = {(z0, z) ∈R (m+1)/ z0 ≥ f(x), z ≥ b – g(x)}
Và đ t S = ặ
x
S(x)
∈Γ
U
. Rõ ràng P, S đ u là t p l i trong R ề ậ ồ (m+1).
2) Đ t Pặ0 = {(z0, z) ∈R (m+1)/ z0 < f(x*), z < 0}. Khi y Pấ0 = intP và do đó P0
cũng là t p l i. Gi s Pậ ồ ả ử 0 ∩ S ≠ ∅. T c là có th tìm th y (z’ứ ể ấ 0, z’) ∈ P0 ∩
S v i z’ớ0 < f(x*), z’ < 0 và z’0 ≥ f(x’), z’ ≥ b – g(x’) ng v i ít nh t m tứ ớ ấ ộ
x’∈Γ. Nh v y, ư ậ x’∈ X và f(x’) < f(x*). Đi u này trái v i gi thi t r ng ề ớ ả ế ằ x*
là l i gi i c a (1.3).ờ ả ủ
3) Do P, S l i và intPồ∩ S = ∅, nên theo đ nh lý tách 3 ch ng I, s t i t iị ươ ẽ ồ ạ
m t siêu ph ng Hộ ẳ α tách P v i S. T c là t n t i (uớ ứ ồ ạ 0,u)∈R (m+1), (u0,u) ≠ 0,
đ choể
∀(z0, z)∈S và ∀(w0, w) ∈P: u0z0 + 〈u, z〉 ≥ u0w0 + 〈u, w〉 ,
Hay u0 (z0 - w0) + 〈u, z - w〉 ≥ 0. (2.7)
Do ∀(z0, z)∈S và ∀(w0, w) ∈P0 thì z0 ≥ f(x) ≥ f(x*) > w0, nên z0–w0 > 0. Từ
đây d dàng suy ra r ng, đ (2.7) đúng ễ ằ ể ∀(z0, z)∈S và ∀(w0, w) ∈P0 thì u0 ≥
0. T ng t , cũng suy ra r ng uươ ự ằ i ≥ 0, i = 1,2,…,m (bài t p…).ậ
4) Ch n ọx∈Γ tùy ý, z0 = f(x), z = b – g(x) và w0 = f(x*), w = 0. T (2.7) suyừ
ra:
∀ x∈Γ: u0 f(x) + 〈u, b – g(x)〉 ≥ u0 f(x*).
(2.8)
N u uế0 = 0, ta có
∀ x∈Γ: 〈u, b – g(x)〉 ≥ 0. (2.9)
Do u ≥ 0, b – g(x) ≤ 0, ∀x∈X, nên trên X: 〈u, b – g(x)〉 = 0. Hay
m
i i i
i 1
u (b g (x)) 0
=− =
∑
, ∀ x∈X
Hay ∀i = 1,2,….,m: ui(bi – gi (x)) = 0, ∀ x∈X. (2.10)
Lê Văn Phi, Khoa Toan Thông kê, Tr ng Đai hoc Kinh tê Tp. Hô Chi Minhươ 47