Chöông 5: THUYEÁT TÖÔNG ÑOÁI HEÏP 139
Chương 5
THUYẾT TƯƠNG ĐỐI HẸP EINSTEIN
Thuyết tương đối hẹp Einstein là một môn cơ học tổng quát, áp dụng cho các
vật chuyển động với vận tốc từ rất bé cho đến cỡ vận tốc ánh sáng và coi cơ học
Newton như một trường hợp giới hạn của mình. Chương này nghiên cứu các tiên đề
của thuyết tương đối hẹp Einstein, phép biến đổi Lorentz cùng các hệ quả của nó và
động lực học tương đối tính của chất điểm chuyển động.
§5.1 CÁC TIÊN ĐỀ CỦA THUYẾT TƯƠNG ĐỐI HẸP EINSTEIN
Cơ học Newton đã đạt được nhiều thành tựu to lớn trong suốt hai thế kỷ đến
nỗi nhiều nhà vật lý trong thế kỷ 19 đã cho rằng việc giải thích một hiện tượng vật lý
bất kỳ đều có thể thực hiện được bằng cách đưa nó về một quá trình cơ học tuân theo
các định luật Newton. Tuy nhiên với sự phát triển của khoa học người ta đã phát hiện
ra các hiện tượng mới không nằm trong phạm vi của cơ học cổ điển. Chẳng hạn, người
ta đã gặp những vật chuyển động nhanh với vận tốc vào cỡ vận tốc ánh sáng trong
chân không (c = 3.108 m/s). Khi đó xuất hiện sự mâu thuẫn với các quan điểm của cơ
học Newton, cụ thể là không gian, thời gian và vật chất phụ thuộc vào chuyển động,
chứ không phải độc lập với chuyển động như Newton quan niệm. Người ta nhận xét
rằng cơ học Newton chỉ đúng đối với các vật chuyển động với vận tốc nhỏ hơn vận tốc
ánh sáng trong chân không rất nhiều. Để mô tả sự chuyển động với vận tốc so sánh
được với vận tốc ánh sáng, Einstein đã xây dựng môn cơ học tương đối tính, gọi là
thuyết tương đối hẹp, vào năm 1905.
Sự đúng đắn của thuyết tương đối hẹp Einstein cho đến nay không cần bàn cãi
gì nữa vì nó đã được thử thách qua vô số thí nghiệm trong suốt thế kỷ qua. Hiện nay
nó trở thành tiêu chuẩn để đánh giá sự đúng đắn của mọi thí nghiệm vật lý. Nếu một
thí nghiệm nào đó mà kết quả mâu thuẫn với thuyết tương đối hẹp thì các nhà vật lý
không đặt vấn đề nghi ngờ thuyết tương đối mà mặc nhiên khẳng định rằng trong thí
nghiệm đặt ra có cái gì đó chưa ổn.
Thuyết tương đối hẹp Einstein xây dựng trên hai nguyên lý là nguyên lý tương
đối Einstein và nguyên lý bất biến của vận tốc ánh sáng. Hai nguyên lý đó phát biểu
như sau:
1. Nguyên lý tương đối Einstein: Mọi định luật vật lý đều như nhau trong
các hệ quy chiếu quán tính.
2. Nguyên lý về sự bất biến của vận tốc ánh sáng: Vận tốc ánh sáng trong
chân không đều bằng nhau theo mọi phương và đối với mọi hệ qui chiếu quán tính. Nó
có giá trị c = 3.108 m/s và là giá trị vận tốc cực đại trong tự nhiên.
Nguyên lý tương đối Einstein là sự mở rộng của nguyên lý tương đối Galilée.
Nguyên lý tương đối Galilée áp dụng cho các hiện tượng cơ học, nói rằng các định
luật cơ học là giống nhau trong các hệ quy chiếu quán tính. Còn nguyên lý Einstein
140 Giaùo Trình Vaät Lyù Ñaïi Cöông Taäp 1: Cô – Nhieät – Ñieän
mở rộng ra cho tất cả các định luật vật lý nói chung. Theo Einstein thì tất cả các định
luật của tự nhiên là như nhau trong tất cả các hệ quy chiếu quán tính. Vậy nguyên lý
tương đối Einstein đã mở rộng nguyên lý tương đối Galilée từ các hiện tượng cơ học
sang các hiện tương vật lý nói chung.
Nguyên lý về sự bất biến của vận tốc ánh sáng phản ảnh rõ ràng sự khác nhau
về vận tốc tương tác trong hai lý thuyết cổ điển và tương đối. Trong lý thuyết tương
đối, vận tốc truyền tương tác là hữu hạn và như nhau trong tất cả các hệ quy chiếu
quán tính. Thực nghiệm chứng tỏ vận tốc không đổi này là cực đại và bằng vận tốc
ánh sáng trong chân không c = 3.108 m/s. Trong cơ học Newton, quan niệm sự tương
tác giữa các vật là tức thời, tức vận tốc tương tác là vô cùng. Điều này giải thích được
do vận tốc trong cơ học cổ điển có giá trị rất bé, v << c. Vì vậy vận tốc ánh sáng có thể
coi là lớn vô cùng trong cơ học cổ điển. Như vậy về mặt hình thức có thể chuyển từ
thuyết tương đối Einstein sang cơ học Newton bằng cách cho c → ∞ trong các công
thức của cơ học tương đối tính.
§5.2. PHÉP BIẾN ĐỔI LORENTZ
1 – Sự mâu thuẫn của phép biến đổi Galilée với thuyết tương đối Einstein
Trong cơ học cổ điển Newton, thời gian là tuyệt đối còn vận tốc tuân theo quy
luật cộng vận tốc. Điều này mâu thuẫn với thuyết tương đối Einstein, trong đó thời
gian phụ thuộc chuyển động và công thức cộng vận tốc (2.68) không còn đúng nữa.
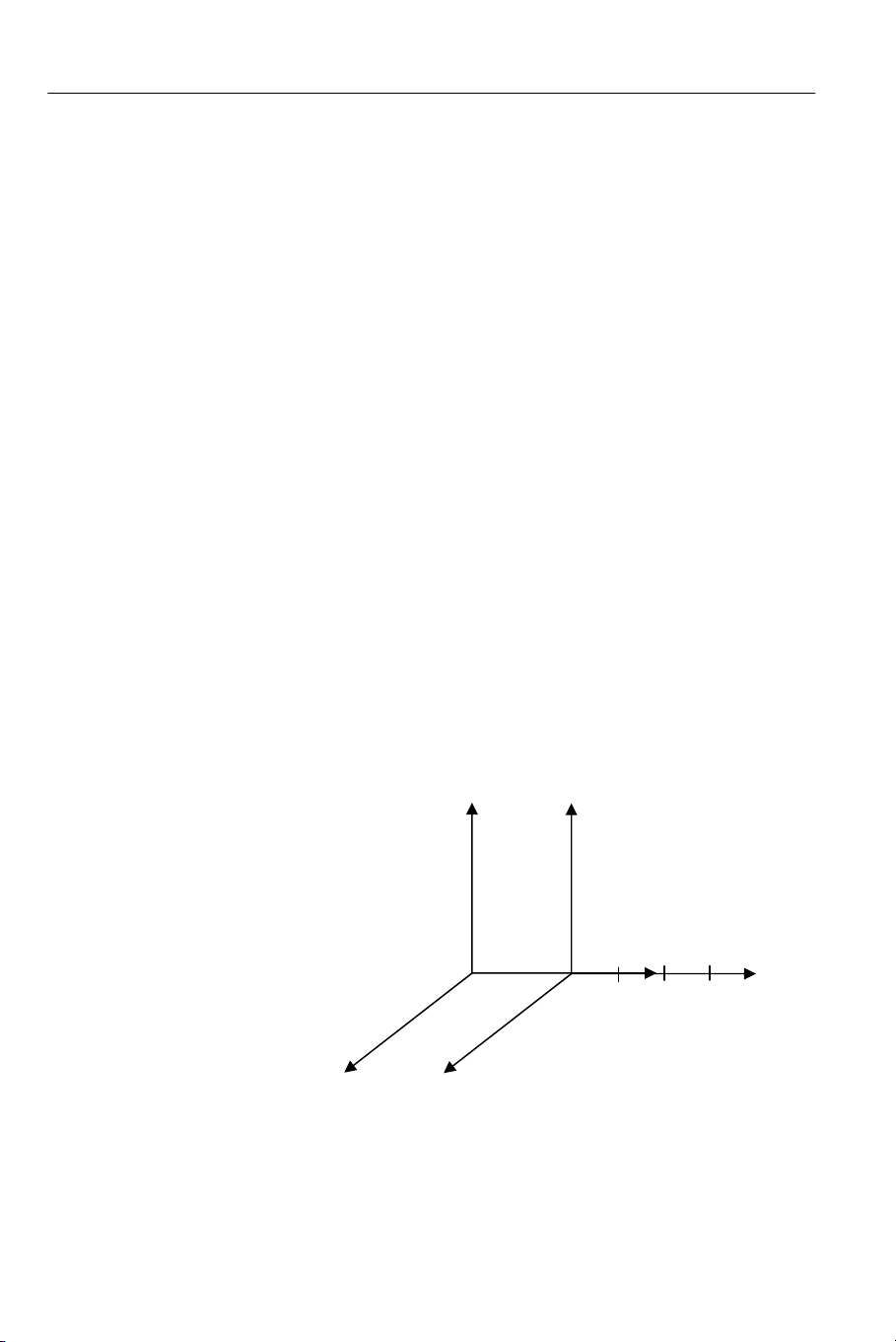
Để chứng minh nhận xét này, ta hãy xét hệ quy chiếu quán tính Oxyz và hệ quy chiếu
quán tính O’x’y’z’ chuyển động dọc theo trục Ox với vận tốc V. Ta đặt một nguồn
sáng tại điểm A trên trục O’x’ trong hệ O’ và hai điểm B và C đối xứng qua A như
trên hình 5.1.
Hình 5.1: Chứng minh sự
mâu thuẫn của phép biến
đổi Galilée với thuyết tương
đối Einstein.
z
O
y
x
B A C
z’
x’
y
’
O’
Trước tiên ta xét công thức công vận tốc (2.68). Theo nguyên lý tương đối
Galilée vận tốc ánh sáng trong hệ O theo chiều dương của trục x sẽ bằng (c + V) còn
theo chiều âm bằng (c – V). Điều đó mâu thuẩn với nguyên lý vận tốc ánh sáng bất
biến đối với các hệ quy chiếu quán tính trong thuyết tương đối.
Bây giờ xét đến mâu thuẫn về tính chất tương đối và tuyệt đối của thời gian.
Đối với hệ O’ thì nguồn sáng A đứng yên vì nó cùng chuyển động với hệ O’. Theo
thuyết tương đối thì vận tốc tín hiệu ánh sáng truyền đi mọi phương đều bằng c nên
Chöông 5: THUYEÁT TÖÔNG ÑOÁI HEÏP 141
trong hệ O’ các tín hiệu sẽ đến các điểm B và C cách đều A cùng một lúc. Nhưng các
tín hiệu sáng sẽ đến các điểm B và C không đồng thời trong hệ O. Trong hệ này vận
tốc truyền ánh sáng vẫn bằng c nhưng vì điểm B chuyển động đến gặp tín hiệu sáng
gửi từ A đến B còn điểm C chuyển động ra xa khỏi tín hiệu gửi từ A đến C, do đó
trong hệ O tín hiệu sáng sẽ gửi tới điểm B sớm hơn. Như vậy trong hệ O, theo thuyết
tương đối thì các điểm B và C nhận tín hiệu sáng không đồng thời, còn theo thuyết cơ
học cổ điển, các tín hiệu sáng đến B và C đồng thời do quan niệm thời gian không phụ
thuộc hệ tọa độ.
2 – Phép biến đổi Lorentz
Phép biến đổi Galilée dẫn tới quy luật cộng vận tốc (2.68), mà quy luật này
mâu thuẫn với nguyên lý về sự bất biến của vận tốc ánh sáng. Như vậy phép biến đổi
Galilée không thỏa mãn các yêu cầu của thuyết tương đối. Phép biến đổi các tọa độ
không gian và thời gian khi chuyển từ hệ quán tính này sang hệ quán tính khác thỏa
mãn các yêu cầu của thuyết tương đối là phép biến đổi Lorentz.
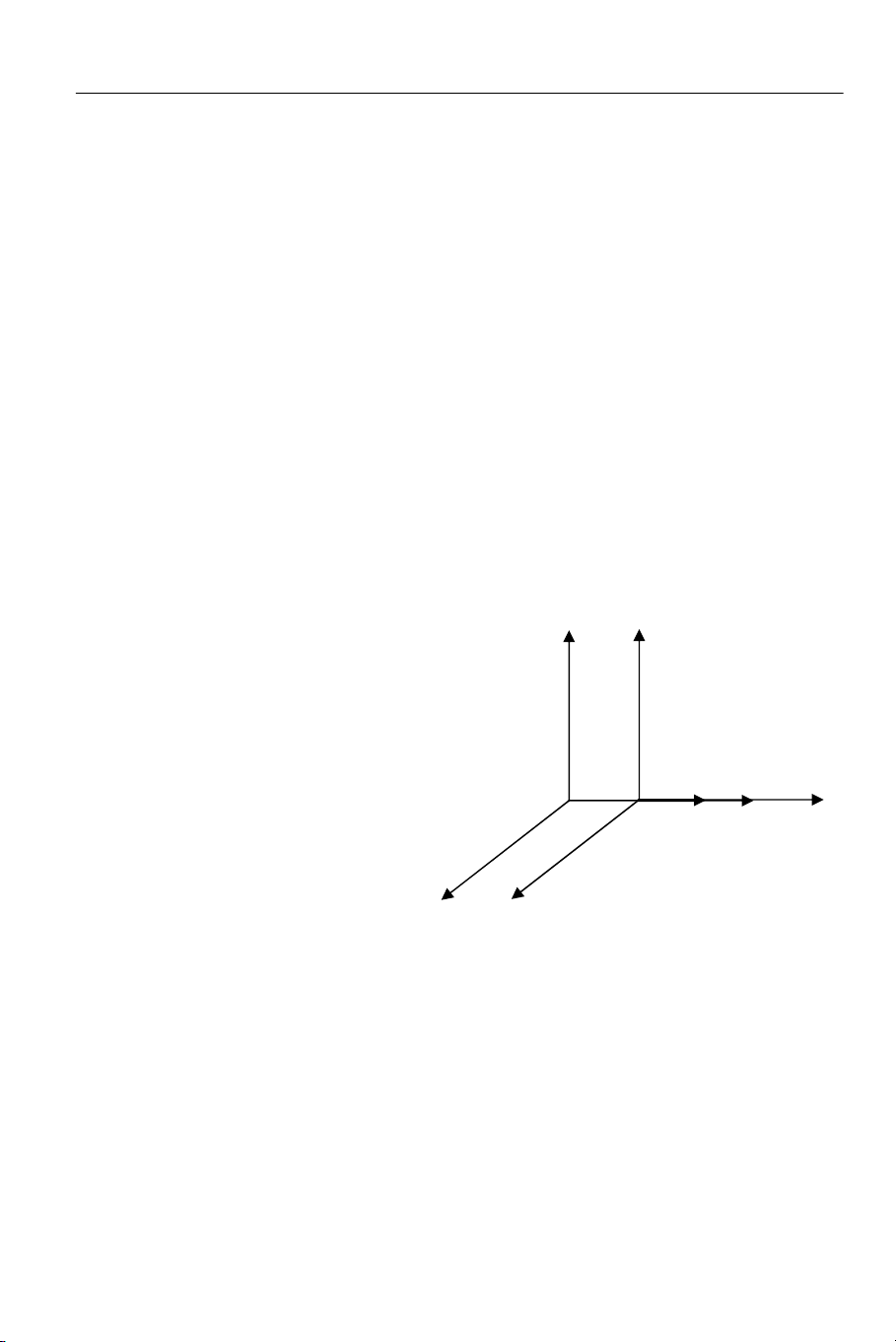
Xét hai hệ quán tính Oxyz và O’x’y’z’, hệ O’ chuyển động so với hệ O với
vận tốc V theo phương x (Hình 5.2). Giả sử lúc đầu hai gốc O và O’ của hai hệ trùng
nhau. Gọi (x,y,z,t) và (x’,y’,z’,t’) là các tọa độ không gian và thời gian trong các hệ O
và O’.
Gốc tọa độ O’ của hệ O’ có tọa độ x’ =
0 trong hệ O’ và x = Vt trong hệ O. Do
đó biểu thức x - Vt phải triệt tiêu đồng
thời với tọa độ x’. Muốn thế phép biến
đổi tuyến tính phải có dạng:
z
O
y
x
V
G
z’
x’
y
’
O’
x’ = α(x – Vt) (5.1)
trong đó α là một hằng số nào đó.
Tương tự, gốc tọa độ O của hệ O có
tọa độ x = 0 trong hệ O và x’ = -Vt’
trong hệ O’. Do đó ta có
x = β(x’ + Vt’) (5.2)
Theo nguyên lý tương đối
Einstein, mọi định luật vật lý đều như
nhau trong các hệ quy chiếu quán tính. Như vậy các phương trình (5.1) và (5.2) có thể
suy ra lẫn nhau bằng cách thay V
⇔
-V, x
⇔
x’ và t
⇔
t’, do đó β = α.
Hình 5.2:Minh họa phép biến đổi
Lorentz.
Theo nguyên lý bất biến của vận tốc ánh sáng, nếu trong hệ O ta có x = ct thì
trong hệ O’ ta có x’ = ct’. Thay các biểu thức này vào (5.1) và (5.2) ta được: ct’ =
α(ct – Vt) = αt(c – V) (5.3a)
ct = α(ct’ + Vt’) = αt’(c + V) (5.3b)
Nhân cả hai hệ thức với nhau ta đi tới phương trình: c2 = α2(c2 – V2)
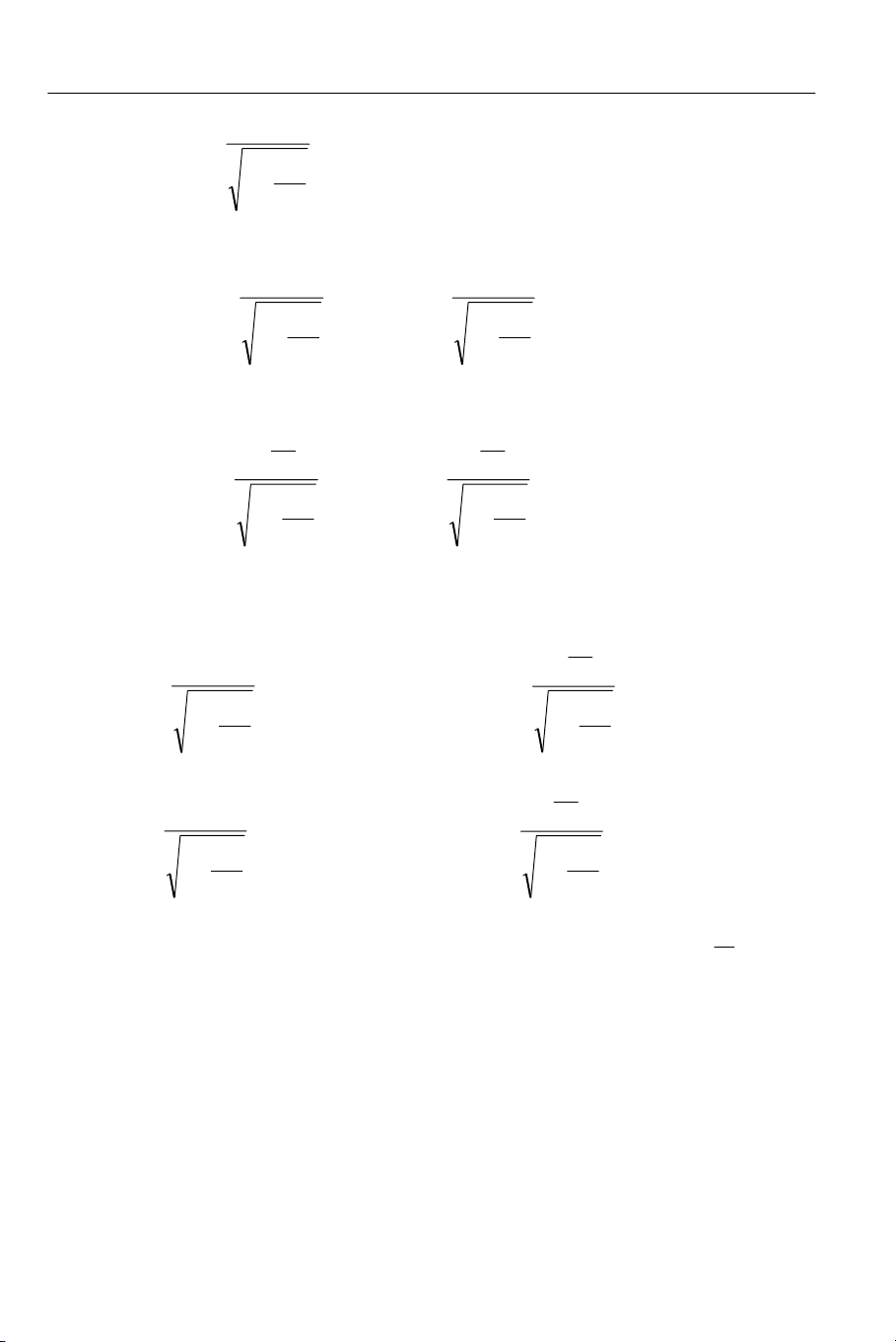
142 Giaùo Trình Vaät Lyù Ñaïi Cöông Taäp 1: Cô – Nhieät – Ñieän
Từ đó ta có:
2
2
1
1
c
V
−
=α (5.4)
Thay α vào (5.1) và β = α vào (5.2) ta được:
2
2
1c
V
Vtx
'x
−
−
=;
2
2
c
V
1
Vt'x'
x
−
+
= (5.5)
Mặt khác sự phụ thuộc giữa t và t’ là:
2
2
2
1c
V
x
c
V
t
't
−
−
=;
2
2
2
c
V
1
x'
c
V
t'
t
−
+
= (5.6)
Do hệ O’ chuyển động dọc theo trục x nên y = y’ và z = z’. Vì vậy ta được các công
thức biến đổi Lorentz như sau:
x’ =
2
2
1c
V
Vtx
−
−; y’ = y; z’ = z; t’ =
2
2
2
1c
V
x
c
V
t
−
−
(5.7)
x =
2
2
c
V
1
Vt'x'
−
+; y = y’; z = z’; t =
2
2
2
c
V
1
x'
c
V
t'
−
+
(5.8)
Từ các biểu thức (5.7) và (5.8) ta thấy rằng khi c → ∞ hay khi c
V→ 0 thì
chúng trở thành: x’ = x – Vt ; y’ = y ; z’ = z ; t’ = t (5.9)
x = x’ + Vt’ ; y = y’ ; z = z’ ; t = t’ (5.10)
nghĩa là trở thành các công thức biến đổi Galiée trong cơ học cổ điển.
§5.3. TÍNH ĐỒNG THỜI VÀ QUAN HỆ NHÂN QUẢ
1 – Tính đồng thời
Trong mục 5.2.1 ta đã xét các tín hiệu sáng từ điểm A đến các điểm B và C
nằm trên trục x’ của hệ O’. Các tín hiệu sáng đến B và C đồng thời trong hệ O’ nhưng
không đồng thời trong hệ O. Để khảo sát một cách tổng quát tính đồng thời trong các
Chöông 5: THUYEÁT TÖÔNG ÑOÁI HEÏP 143
hệ quy chiếu quán tính, ta giả sử rằng trong hệ O có hai sự kiện A1(x1,y1,z1,t1) và
A2(x2,y2,z2,t2) với x2 ≠ x1. Hệ O’ chuyển động với vận tốc V so với hệ O theo trục x.
Khoảng thời gian trong hệ O là t2 – t1. Khi đó khoảng thời gian của hai sự kiện này
trong hệ O’ là:
t’2 – t’1 =
2
2
12
2
12
1c
V
)xx(
c
V
tt
−
−−−
(5.11)
Từ (5.11) thấy rằng, nếu hai sự kiện A1 và A2 xảy ra đồng thời trong hệ O, nghĩa là t2
= t1, hay t2 – t1 = 0, thì trong hệ O’ ta có t’2 ≠ t’1, tức là hai sự kiện A1 và A2 không xảy
ra đồng thời trong hệ O’, trừ trường hợp x2 = x1.
Vậy khái niệm đồng thời là khái niệm tương đối, hai sự kiện có thể xảy ra
đồng thời trong hệ quán tính này nhưng không đồng thời trong hệ quán tính khác.
2 – Quan hệ nhân quả
Liên hệ nhân quả là một liên hệ giữa nguyên nhân và kết quả. Nguyên nhân
bao giờ cũng xảy ra trước kết quả, quyết định sự ra đời của kết quả. Giả sử sự kiện
A1(x1, t1) là nguyên nhân và A2(x2, t2) là kết quả thì t2 > t1. Để xét trong hệ O’, ta chú ý
rằng trong hệ O thì x1 = vt1 và x2 = vt2, do đó
t’2 – t’1 =
2
2
12
2
12
1c
V
)vtvt(
c
V
tt
−
−−−
=
2
2
2
12
1
1
c
V
c
Vv
)tt(
−
⎟
⎠
⎞
⎜
⎝
⎛−−
(5.12)
Do v < c và V < c nên khi t2 > t1 ta có t’2 > t’1. Như vậy trong hệ O’, sự kiện A1 cũng
là nguyên nhân và sự kiện A2 cũng là kết quả. Vậy thứ tự nhân quả được tôn trọng
trong các hệ quy chiếu quán tính.
§5.4 SỰ CO NGẮN LORENTZ
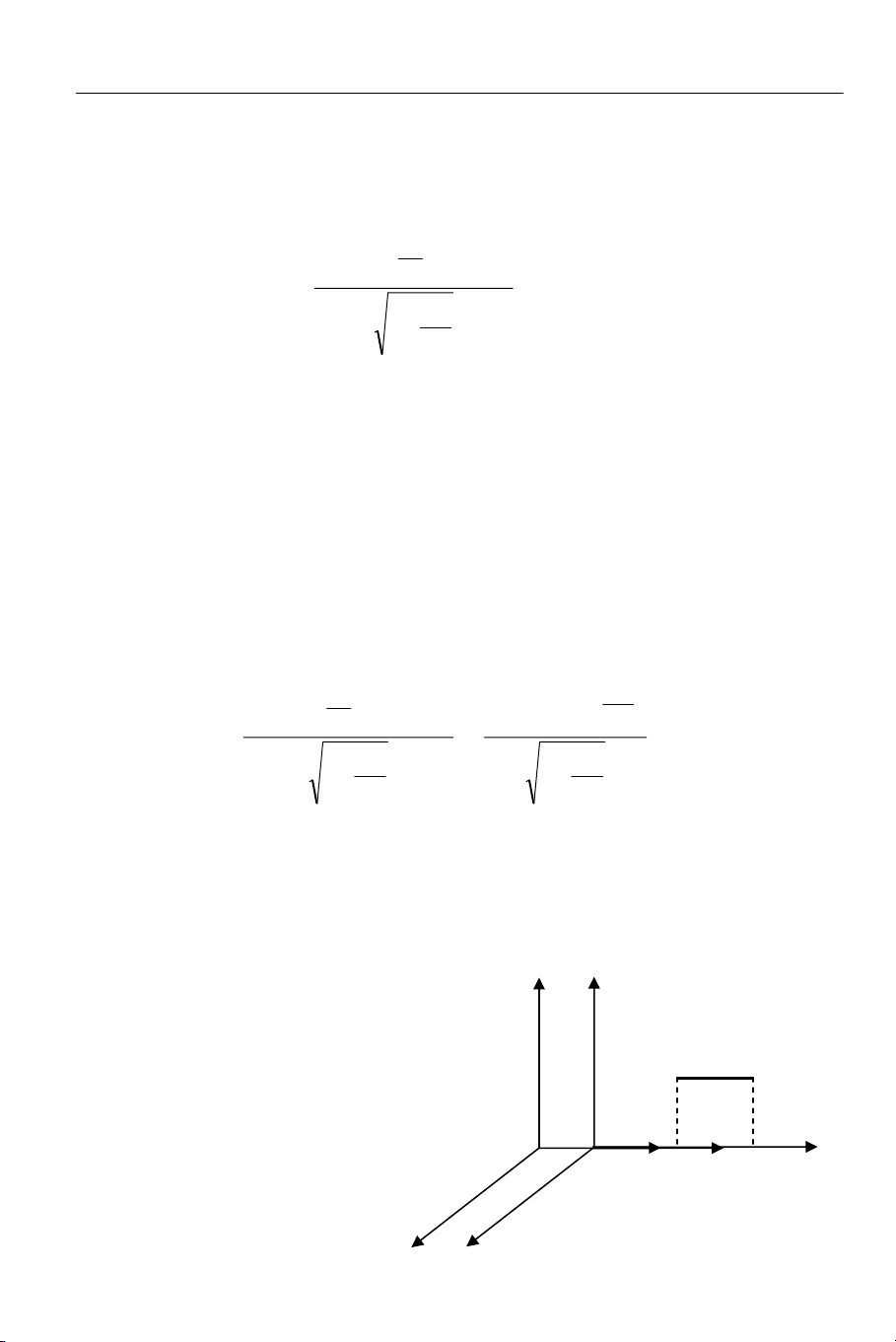
Ta hãy so sánh độ dài và
khoảng thời gian trong hai hệ quán
tính O và O’.
Hình 5.3: Minh họa sự co ngắn
Lorentz.
z
O
y
x
z’
x’
y
’
O’
1 2
x
2
x’
2
x
1
x’
1
1 – Độ dài:
Giả sử có một thanh đứng
yên trong hệ O’ (Hình 5.3), đặt dọc
theo trục O’x’, độ dài của nó trong
hệ O’ là: ∆x’ = x’2 – x’1
Độ dài của nó trong hệ O là:
∆x = x2 – x1.