
Chuyên đề khảo sát hàm số ồ Văn Hoàng
1
Chuyên đề : Khảo sát hàm số và ứng dụng
Các bài toán liên quan đến khảo sát hàm số .
1.Dạng 1:Viết phương trình tiếp tuyến tại điểm M(xM ; yM) .
B1 : hệ số góc tiếp tuyến k = f ‘(xM) .
B2 :Phương trình tiếp tuyến : y – yM = k(x – xM ) .
2.Dạng 2:Viết phương trình tiếp tuyến khi biết dạng của tiếp tuyến
với đồ thị.
B1: Tìm dạng của tiếp tuyến y = g(x) .
B2: Điều kiện tiếp xúc :
( ) ( )
'( ) '( )
f x g x
f x g x
Chú ý :
a. (C) : y = f(x), tx (C/) : y = g(x) khi hệ phương trình sau có
nghiệm :
/
/
/ /
CC
CC
y y
y y
. Nghiệm x của hệ là hoành độ tiếp điểm.
b. Tìm tiếp tuyến với (C) : y = f(x)
*Tại M(xo, yo) : y = f'(xo)(x – xo) + yo.
*Qua M (xo, yo): viết phương trình đường thẳng qua M :
(d): y = k(x – xo) + yo. Dùng điều kiện tx tìm k. Số lượng k = số
lượng tiếp tuyến (nếu f bậc 3 hay bậc 2 / bậc 1 thì số nghiệm x
trong hệ phương trình đk tx = số lượng tiếp tuyến).
* // () : y = ax + b : (d) // () (d) : y = ax + m.
* () : y = ax + b (a 0) : (d) () (d) : y =
1
a
x + m.
Tìm m nhờ đk tx.
c. Bài toán số lượng tiếp tuyến : tìm M (C/) : g(x, y) = 0 sao
cho từ M kẻ được đến (C) đúng n tiếp tuyến (n = 0, 1, 2, ...),
M(xo,yo)(C/)g(xo,yo) = 0; (d) qua M: y = k(x –xo) + yo
(d) tx (C) :
/
C d
C
y y
y k
(1).
Thế k vào (1) được phương trình ẩn x, tham số xo hay yo.
Đặt đk để phương trình có n nghiệm x (số nghiệm x = số tiếp
tuyến), tìm được xo hay yo.
3.Dạng 3:Đường cong : y = ax3 + bx2 + cx + d cắt Ox tại ba điểm
phân biệt khi : ax3 + bx2 + cx + d = 0 có ba nghiệm phân biệt
hay yCĐ .yCT < 0 .
4.Dạng 4:. Điểm đặc biệt của (Cm) : y = f(x, m)
a/ Điểm cố định : M(xo, yo) (Cm), m yo = f(xo, m), m
Am + B = 0, m (hay Am2 + Bm + C = 0, m)
0
0
A
B
(hay
0
0
0
A
B
C
). Giải hệ, được M.
b/ Điểm (Cm) không đi qua, m : M(xo, yo) (Cm), m
yo f(xo,m), m
yo = f(xo, m) VN m Am + B = 0 VN m (hay Am2 + Bm +
C = 0 VN m)
0
0
A
B
(hay
00
00
0
AA
B
C
).
Giải hệ , được M. Chú ý :
AC
B
VN B = 0
0B
A BC VN
c/ Điểm có n đường cong của họ (Cm) đi qua : Có n đường
(Cm) qua M(xo, yo) yo = f(xo, m) có n nghiệm m.
Cần nắm vững điều kiện có n nghiệm của các loại phương trình :
bậc 2, bậc 2 có điều kiện x , bậc 3, trùng phương.
d/Tìm điểm M © : y = ax + b +
c
dx e
có tọa độ nguyên
(a, b, c, d, e Z) : giải hệ
,
M M
M
M M
c
y ax b dx e
x y Z
,
M M
M
M
M
c
y ax b dx e
c
x Z
dx e
,
M M
M
M M
c
y ax b dx e
x Z dx e c
öôùc cuûa
5.Dạng 5:TÂM, TRỤC, CẶP ĐIỂM ĐỐI XỨNG :
a. Cmr đồ thị hàm số nhận điểm M(xM ; yM) làm tâm đối xứng
B1: Đặt
M
M
x x X
y y Y
thay vào y = f(x) và đưa về dạng Y = F(X)
B2: Ta chứng minh hàm số Y = F(X) lẻ (tức là F(-X) = - F(X) )
trên tập xác định nên nhận
0
0
M
M
x x
X
Y y y
làm tâm đối xứng
hàm bậc 3 có tâm đx (điểm uốn), hàm phân thức (gđ 2 tc) tại I :
b. CM hàm bậc 4 có trục đx // (Oy) : giải pt y/ = 0; nếu x = a là
nghiệm duy nhất hay là nghiệm chính giữa của 3 nghiệm :
đổi tọa độ x = X + a, y = Y; thế vào hàm số : Y = F(X);
cm F(–X) = F(X); suy ra F là hàm chẵn, đồ thị có trục đối xứng là
trục tung X = 0 x = a
c. Tìm trên (C) : y = f(x) cặp điểm M, N đối xứng qua I .
giải hệ 4 pt 4 ẩn :
2
2
( )
( )
M N I
M N I
M M
N N
x x x
y y y
y f x
y f x
d. Tìm trên (C) : y = f(x) cặp điểm đ/x qua đt (d) : y = ax +
b :
dt (d) là (d') : y = –
1
a
x + m; lập pt hđ điểm chung của (C) và
(d'); giả sử pt có 2 nghiệm xA, xB, tính tọa độ trung điểm I của
AB theo m; A, B đối xứng qua (d) I (d) m?;
thay m vào pthđ điểm chung, giải tìm xA, xB, suy ra yA, yB.
Tìm tọa điểm uốn : B1: y’’ = 0 có nghiệm xo
yo = f(xo)
B2: Tọa độ điểm uốn : U(xo;yo) .
6.Dạng 6:ĐƠN ĐIỆU :
a. Biện luận sự biến thiên của hàm bậc 3 :
i) a> 0 và y’ = 0 vô nghiệm hàm số tăng trên R (luôn tăng)
ii) a< 0 và y’ = 0 vô nghiệm hàm số giảm trên R (luôn giảm)
iii)a > 0 và y’ = 0 có 2 nghiệm phân biệt x1, x2 với x1 < x2
hàm số đạt cực đại tại x1 và đạt cực tiểu tại x2. Ngoài ra ta có :
+ x1 + x2 = 2x0 với x0 là hoành độ điểm uốn.
+ hàm số tăng trên (, x1); + hàm số tăng trên (x2, +);
+ hàm số giảm trên (x1, x2)
iv)a < 0 và y’ = 0 có 2 nghiệm phân biệt x1, x2 với x1 < x2
hàm đạt cực tiểu tại x1 và đạt cực đại tại x2 thỏa điều kiện x1
+ x2 = 2x0 (x0 là hoành độ điểm uốn). Ta cũng có :
+ hàm số giảm trên (, x1); + hàm số giảm trên (x2, +);
+hàm số tăng trên (x1, x2)
b. Biện luận sự biến thiên của y =
2
ax bx c
mx n
i) Nếu a.m > 0 và y/ = 0 vô nghiệm thì hàm tăng ( đồng biến) trên
từng khỏang xác định.
ii) Nếu a.m < 0 và y/ = 0 vô nghiệm thì hàm giảm (nghịch biến)
trên từng khỏang xác định.
Chuyên đề khảo sát hàm số Hồ Văn Hoàng
2
iii) Nếu a.m > 0 và y/ = 0 có 2 nghiệm phân biệt x1, x2thì hàm đạt
cực đại tại x1 và đạt cực tiểu tại x2 thỏa x1< x2 và
1 2
2
x x p
m
.
iv) Nếu a.m < 0 và y/ = 0 có 2 nghiệm phân biệt x1, x2 thì hàm đạt
cực tiểu tại x1 và đạt cực đại tại x2 thỏa x1 < x2 và
1 2
2
x x p
m
.
c.Tìm m để hàm số bậc 3, bậc 2/bậc 1 đồng biến
(nghịch biến) / miền xI: đặt đk để I nằm trong miền đồng
biến (nghịch biến) của các BBT trên; so sánh nghiệm pt y/ = 0
với .
7.Dạng 7:Tìm giá trị lớn nhất của hàm số và giá trị nhỏ nhất của
hàm số .
Trên khoảng (a ; b) thì ta lập bảng xét dấu của y’ và yCĐ là
GTLN; yCT là GTNN .
Trên đoạn [a ; b] thì ta giải phương trình :y’ = 0 có nghiệm x1 ;
x2 ; … thuộc [a ; b]
Tính y(x1) ; y(x2) ; … ; y(a) ; y(b) .Số lớn nhất là GTLN ; số nhỏ
nhất là GTNN.
8.Dạng8: Cực trị f có đúng n cực trị f/ đổi dấu n lần.
f đạt cực đại tại xo
/
//
( ) 0
( ) 0
o
o
f x
f x
;
f đạt cực tiểu tại xo
/
//
( ) 0
( ) 0
o
o
f x
f x
1/ Hàm bậc 3 (hay bậc 2 / bậc 1) có cực trị
phương trình y’ = 0 có 2 nghiệm phân biệt
*Tính yCĐ.yCT :
Hàm bậc 3 : y = y/ (Ax + B) + (Cx+ D);
yCĐ.yCT = (CxCĐ + D).(CxCT + D), dùng Viète với pt y/ = 0.
Hàm bậc 2/ bậc 1 :
u
yv
; yCĐ.yCT =
/ /
/ /
( ). ( )
( ). ( )
CÑ CT
CÑ CT
u x u x
v x v x
,
dùng Viète với pt y/ = 0.
2/ Hàm trùng phương: y = ax4 + bx2 + c có 1 cực trị ab 0,
3 cực trị ab < 0
9.Dạng 9:Viết phương trình đường thẳng đi qua điểm cực đại và
điểm cực tiểu (cực trị)
a) Hàm phân thức : y =
2
ax bx c
dx e
=
( )
( )
f x
g x
.
B1: Điều kiện để có cực trị là y’ = 0 có hai nghiệm phân biệt .
B2: có 2 nghiệm xCĐ ; xCT thì yCĐ =
'( )
'( )
CD
CD
f x
g x
& yCT =
'( )
'( )
CT
CT
f x
g x
B3:Kết luận :Đường thẳng qua cực trị là : y =
'( )
'( )
f x
g x
.
b) Hàm đa thức :y = ax3 + bx2 + cx + d .
B1:Điều kiện để có có cực trị là y’ = 0 có hai nghiệm phân biệt .
B2:Chia đa thức :Lấy y chia y’ .Kết quả có dạng :
y = y’(x) .[
1
3 9
b
xa
] +
2
2(3 ) 9
.
9 9
ac b ad cb
x
a a
.
B3:Giả sử có hai nghiệm xCĐ ; xCT thì
yCĐ =
2
2(3 ) 9
.
9 9
CD
ac b ad cb
x
a a
; yCT =
2
2(3 ) 9
.
9 9
CT
ac b ad cb
x
a a
B4:Kết luận :đường thẳng qua cực trị là:y =
2
2(3 ) 9
.
9 9
ac b ad cb
x
a a
.
10.Dạng 10:Vẽ đồ thị hàm số có chứa dấu giá trị tuyệt đối .
1) Hàm số y = f(|x|) .
Phương pháp :
B1: Vẽ đồ thị hàm số y = f(x) .
B2: Giữ nguyên phần x ≥ 0 , lấy đối xứng phần x > 0 qua Oy
2) Hàm số y = |f(x)| .
Phương pháp :
B1: Vẽ đồ thị hàm số y = f(x) .
B2: Giữ nguyên phần y ≥ 0 , lấy đối xứng phần y <0 qua Ox3)
Hàm số y = |f(|x|)| .
Phương pháp :
B1: Vẽ đồ thị hàm số y = f(x) .
B2: Giữ nguyên phần x ≥ 0 , lấy đối xứng phần x >0 qua Oy
B3: Giữ nguyên phần y ≥ 0 , lấy đối xứng phần y < 0qua Ox
Nhớg(x) = f(–x) : đối xứng qua (Oy);
g(x) = – f(x) : đối xứng qua (Ox).
11. Dạng 11: Bài toán tìm quỹ tích .
B1: Tìm toạ độ quỹ tích M
( )
( )
x f m
y g m
.
B2:Khử tham số m giữa x và y ta có phương trình quỹ tích .
B3:Giới hạn quỹ tích là dựa vào điều kiện của tham số m , suy ra
điều kiện của x và y .
Nếu xo = a thì M (d) : x = a.
Nếu yo = b thì M (d) : y = b.
12.Dạng 12 : Bài toán TƯƠNG GIAO :
*Phương trình hđ điểm chung của (C) : y = f(x) và (C/) : y = g(x)
là : f(x) = g(x). Số nghiệm pt = số điểm chung.
*Tìm m để (Cm) : y = f(x, m) và (C/m) : y = g(x, m) có n giao
điểm : Viết phương trình hoành độ điểm chung; đặt đk để pt có n
nghiệm. Nếu pt hoành độ điểm chung tách được m sang 1 vế :
F(x) = m; đặt điều kiện để (C):y=F(x) & (d): y = m có n điểm chung.
*Biện luận sự tương giao của (Cm) và (C/m) :
Nếu pt hđ điểm chung dạng : F(x) = m : lập BBT của F; số
điểm chung của (Cm) và (C/m) = số điểm chung của (C) và (d).
PThđ điểm chung, không tách được m, dạng ax2 + bx + c = 0
(x ) hay dạng bậc 3 : x = f(x) = 0 : lập , xét dấu , giải
pt f(x) = 0 để biết m nào thì là nghiệm của f, với m đó, số
nghiệm bị bớt đi 1.
Bài toán đồ thị hàm số y = ax4 + bx2 + c cắt trục hoành tại 4
điểm phân biệt có hoành độ lập thành 1 cấp số cộng .
B1:Phương trình hoành độ giao điểm của ( C) với trục hoành là
ax4 + bx2 + c = 0 (1).
Đặt t = x2 (điều kiện :t > 0) .Khi đó phương trình (1) trở thành :
at2 + bt + c = 0 (2).
Điều kiện để (C ) cắt trục hoành tại 4 điểm thì phương trình (1)
có 4 nghiệm phân biệt
phương trình (2) có 2 nghiệm dương
phân biệt
0
0
0
S
P
B2:Giả sử (2) có hai nghiệm là 0 < n < m.thì phương trình (1) có
4 nghiệm là :
; ; ;m n n m
.
Để 4 nghiệm lập thành 1 cấp số cộng thì
2m n n
m = 9n (3) .
B3:Ap dụng định lí viet :
.
n m S
n m P
(4) .
Kết hợp (3) và (4) để tìm m và n .Từ đó suy ra cấp số cộng :
; ; ;m n n m
.
BIỆN LUẬN SỐ NGHIỆM PT BẰNG ĐỒ THỊ :
a. Cho pt : F(x, m) = 0; tách m sang 1 vế : f(x) = m; lập BBT của
f (nếu f đã khảo sát thì dùng đồ thị của f),
số nghiệm = số điểm chung.
b. Với pt mũ, log,
, .
, lượng giác: đổi biến; cần biết mỗi
biến mới t được mấy biến cũ x; cần biết đk của t .
1/ Giải bất phương trình bằng đồ thị :
f < g a < x < b, f > g
x a
b x
f g a x b , f g
x a
x b
2/ Tìm 2 điểm thuộc hai nhánh đồ thị sao cho khoảng cách đó là
ngắn nhất .
B1: Từ y =
( )
( )
f x
g x
đổi hệ trục toạ độ Y =
a
X
(với a là hằng số ).
a
b
f
g
Chuyên đề khảo sát hàm số Hồ Văn Hoàng
3
B2: Lấy A
;a
và B
;a
với
0; 0
.
Ví dụ 1. Cho hàm số y = f(x) = mx3 + 3mx2 (m 1)x 1
a) Khảo sát và vẽ đồ thị hàm số với m = 1.
b) Xác định m để hàm y = f(x) không có cực trị
Giải.a) với m = 1, y = x3 + 3x2 1
b) y’ = 3mx2 + 6mx (m 1). Điều kiện cần vàđủ để y = f(x)
không có cực trịlà phương trình f’ (x) = 0 không có hai nghiệm
phân biệt, nghĩa là
2
01
004
' 9 3 ( 1) 0
m
mm
m m m
Ví dụ 2. Cho hàm số y = x3 + mx2 m
a) Khảo sát và vẽ đồ thị hàm số khi m = 3
b) Khi nào đồ thị cắt trục hoành tại 3 điểm phân biệt
c) Xác định m sao cho x 1 y 1.
Giải a) m = 3 y = x3 + 3x2 3
b) Đồ thị cắt trục hoành tại 3 điểm phân biệt khi và chỉ khi hàm
số có cực đại và cực tiểu và ycđ. yct < 0
y’ = 3x2 + 2mx = x(3x + 2m). y’ = 0 x = 0 và x = 2m/3
Hàm có cực đại và cực tiểu 2m/3 0 m 0
3
c®
4 27
. 0 . 2 / 3 0
27
ct
m m
y y y y m m
2
4 27 0m
3 3
2
m
Vậy đồ thị cắt Ox tại 3điểm phân biệt
3 3 / 2m
c)
1y x
với
1x
0 1y m
.
Với
1m
, m 0, ta có
2 / 3 1m
.
với m [1, 1]\
0
để
1y x
với
1x
điều kiện đủ là
3
4
1 2 / 3 27
m
y m m
(vì y (1) = 1, y(1) = 1, y (0) = mđều thuộc [1, 1]).
Nhưng
3 2
4 4
, 1 1
27 27
m m
m m
khi
1m
.
m = 0 cũng thỏa mãn. Kết luận m [1, 1].
Ví dụ 3. Cho hàm số y = (m 2)x3 mx + 2 (1)
a) Khảo sát và vẽ đồ thị hàm số khi m = 1
b) C minh rằng khi m (0, 2) hàm không có cực đại và cực tiểu.
c) C minh rằng đồ thị của hàm số (1) luôn qua ba điểm cố định.
Giảib) y’ = 3(m 2)x2 m
m (0, 2) m / 3(m 2) < 0 và phương trình y’ = 0 vô nghiệm.
c) y = mx3 2x3 mx + 2 mx (x2 1) 2(x3 1) y = 0
Phương trình đúng với mọi m R
2
3
0 2
1 0 1 4
2 1 1 0
o o
o o
o o
o o o o
x y
x x x y
y x x y
Đồ thị luôn đi qua 3 điểm cố định (0, 2), ( 1, 4), (1, 0).
Ví dụ 4. Cho y = f(x) = 2x3 3(2m + 1)x2 + 6m (m + 1)x + 1(1)
a) Tìm quĩ tích điểm uốn
b) Tìm quĩ tích điểm cực đại
c) Tìm quĩ tích trung điểm đoạn nối điểm CĐ& CT của đồ thị.
Giải.a) y’ = 6x2 6(2m + 1) x + 6m(m + 1)
y” = 12x 6(2m + 1), y” = 0
2 1
2
m
x
y” đổi dấu khi x biến thiên qua (2m + 1)/2.
Vậy điểm uốn là
2 1 2 1
,
2 2
m m
U f
.
Từ
2 1
2
m
x
suy ra
2 1
2
x
m
,
thay vào phương trình y = f(x) ta thu được
33
2 1.
2
y x x
Vậy quĩ tích đồ thị hàm
33
2 1.
2
y x x
b) y’ = 6[x2 (2m + 1)x + m (m + 1)], y’ = 0
1
x m
x m
Đó là hai nghiệm phân biệt và rõ ràng
y’(x)<0 x (m, m + 1); y’(x)>0 x(, m) (m + 1, +)
Vậy hàm luôn có cực đại và cực tiểu tại x = m và x = m + 1.
Điểm cực đại là (m, f(m)). Khử m bằng cách thay m = x, vào (1)
ta được y = 2x3 + 3x2 + 1. Vậy đồ thị của hàm y = 2x3 + 3x2 + 1
là quĩ tích các điểm cực đại của hàm số khi m thay đổi.
c) Trung điểm của đoạn nối điểm cực đại và cực tiểu làđiểm uốn,
mà quĩ tích đã biết ở câu a).
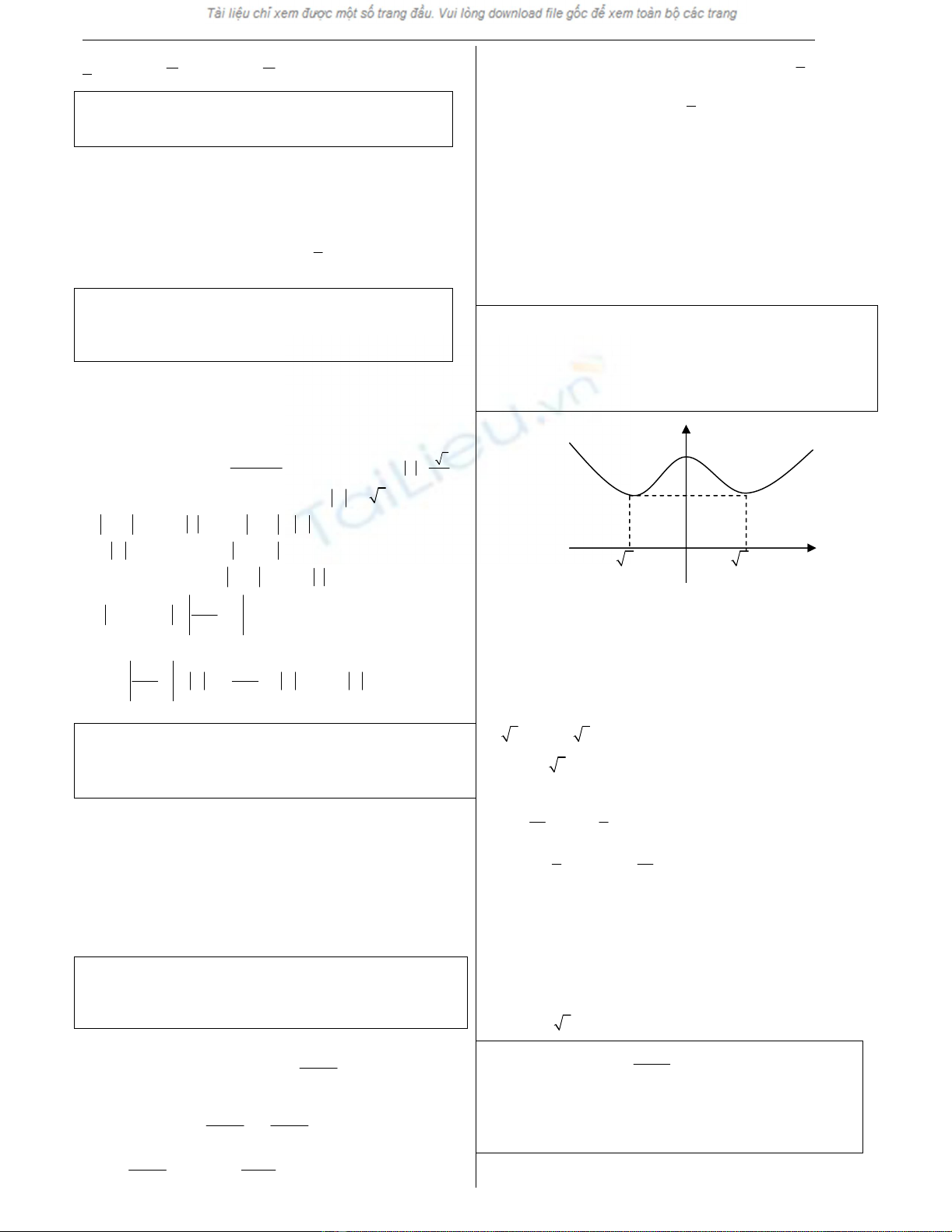
Ví dụ 5. Cho hàm số y = f(x) = x4 mx3 (2m + 1)x2 + mx + 1
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số với a = 0.
b) Tìm các điểm trên trục tung sao cho qua đó có thể kẻ được ba
tiếp tuyến với đồ thị của y = f(x) với m = 0.
c) Xác định m sao cho phương trình f(x) = 0 có hai nghiệm khác
nhau lớn hơn 1.
Giải.a) Với m = 0, hàm số có dạng y = x4 x2 + 1
y
1
3/4
-
2
/2 0
2
/2 x
b) f(x) là hàm chẵn nên trục tung là trục đối xứng. Nên qua điểm
trên trục tung kẻ được ba tiếp tuyến với đồ thị thì phải có 1 tiếp
tuyến song song với trục hoành. Từ đó điểm cần tìm phải làđiểm
M(0, 1). Ta kiểm tra điều đó.
Giả sử y = ax + 1 là tiếp tuyến khác qua a. Khi đó phải có
4 2
3
1 1
4 2
o o o
o o
x x ax
x x a
với xo là hoành độ tiếp điểm.
Giải hệ đó (đối với (xo, a)) ta có các nghiệm (0, 0), và
3 / 3, 4 3 / 9 .
Từ đó các tiếp tuyến khác y = 1 là
4 3 / 9 1y x
.Vậy điểm cần tìm là M (0, 1).
c) Phương trình x4mx3 (2m + 1)x2 + mx + 1 = 0 (1)
2
2
1 1 2 1 0x m x m
x
x
(2)
Đặt
1
t x x
. t’(x) =
2
1
1x
> 0, do đó x > 1 thì t(x) > t(1) = 0.
Bây giờ (2) có dạng t2 mt (2 1) = 0. (3)
Vậy để có hai nghiệm lớn hơn 1, phương trình (3) phải có hai
nghiệm dương. Tức là phải có
22
4 1 2 0 8 4 0
/ 2 / 2 0 0
1 2 0 1/ 2
m m m m
S m m
p m m
4 2 5,1/ 2m
Ví dụ 6. Cho hàm số
1mx
yx m
(1)
a) Khảo sát và vẽ đồ thị hàm số với m = 2.
b) Với m nào hàm đồng biến, nghịch biến không đổi?
c) Cm rằng khi m thay đổi đồ thị luôn đi qua hai điểm cố định.
d) Tìm quĩ tích tâm đối xứng của đồ thị.


























