1
Bài 7
C NH TRANH ĐQẠ
VÀ ĐQ NHÓM
2
I. C NH TRANH Đ C QUY NẠ Ộ Ề
1. Đ c đi m c a TT c nh tranh ĐQặ ể ủ ạ
- Có nhi u ng i bán t do gia nh p hay xu t ề ườ ự ậ ấ
ngành, th ph n m i DN r t nh , không đáng k ị ầ ỗ ấ ỏ ể
trên TT.
- SP phân bi t v i nhau qua nhãn hi u, ki u ệ ớ ệ ể
dáng, ch t l ng…có kh năng thay th nh ng ấ ượ ả ế ư
k0 hoàn toàn.
- K0 có m t m c P duy nh t cho t t c SP.ộ ứ ấ ấ ả
1. Đ c tr ng c b n c a c nh tranhặ ư ơ ả ủ ạ
ĐQ
3
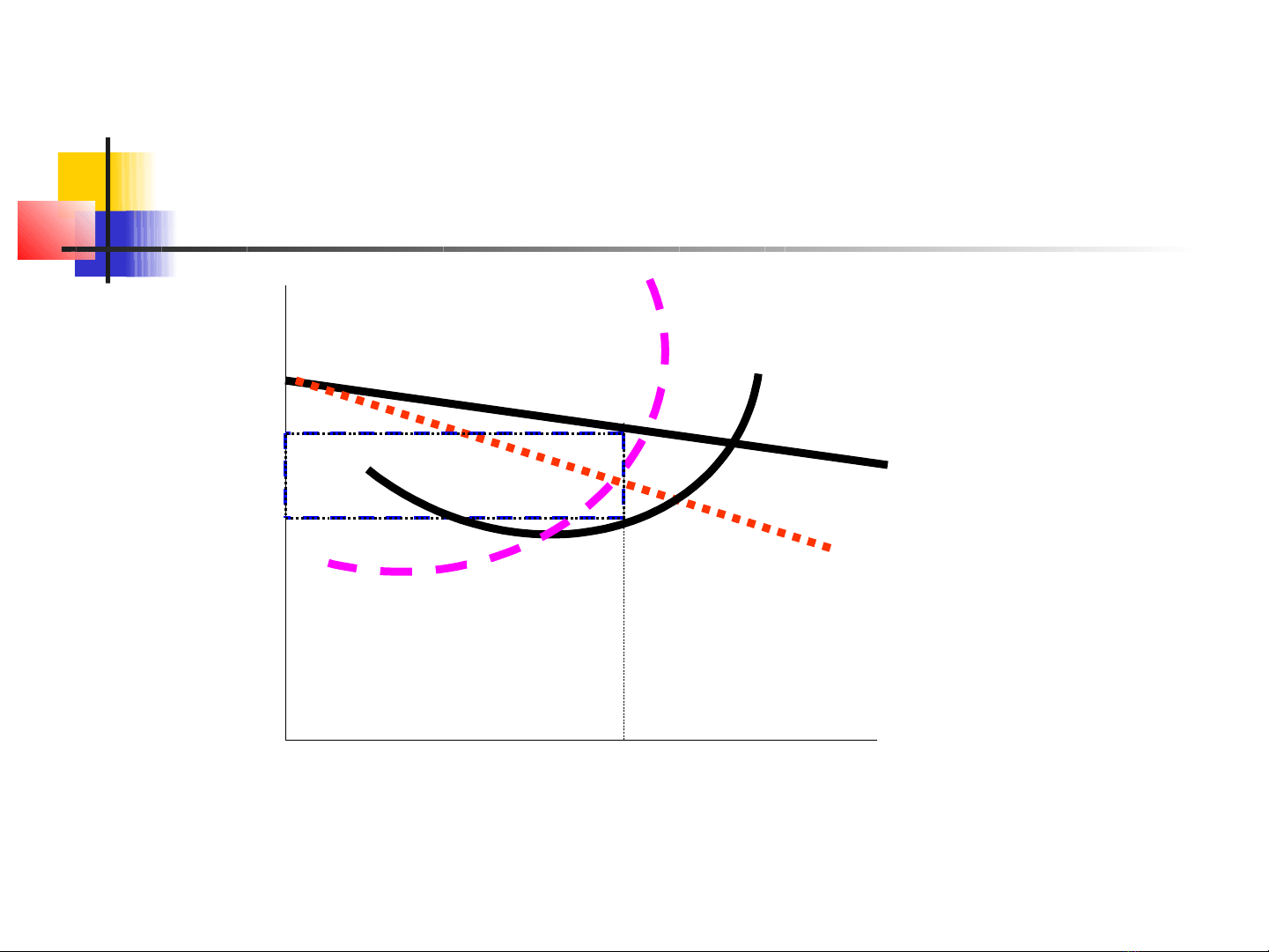
2. Cân b ng ng n h n c a DNằ ắ ạ ủ
Q
P
AR
MR
P
C
Q
A
B
AC
MC
4
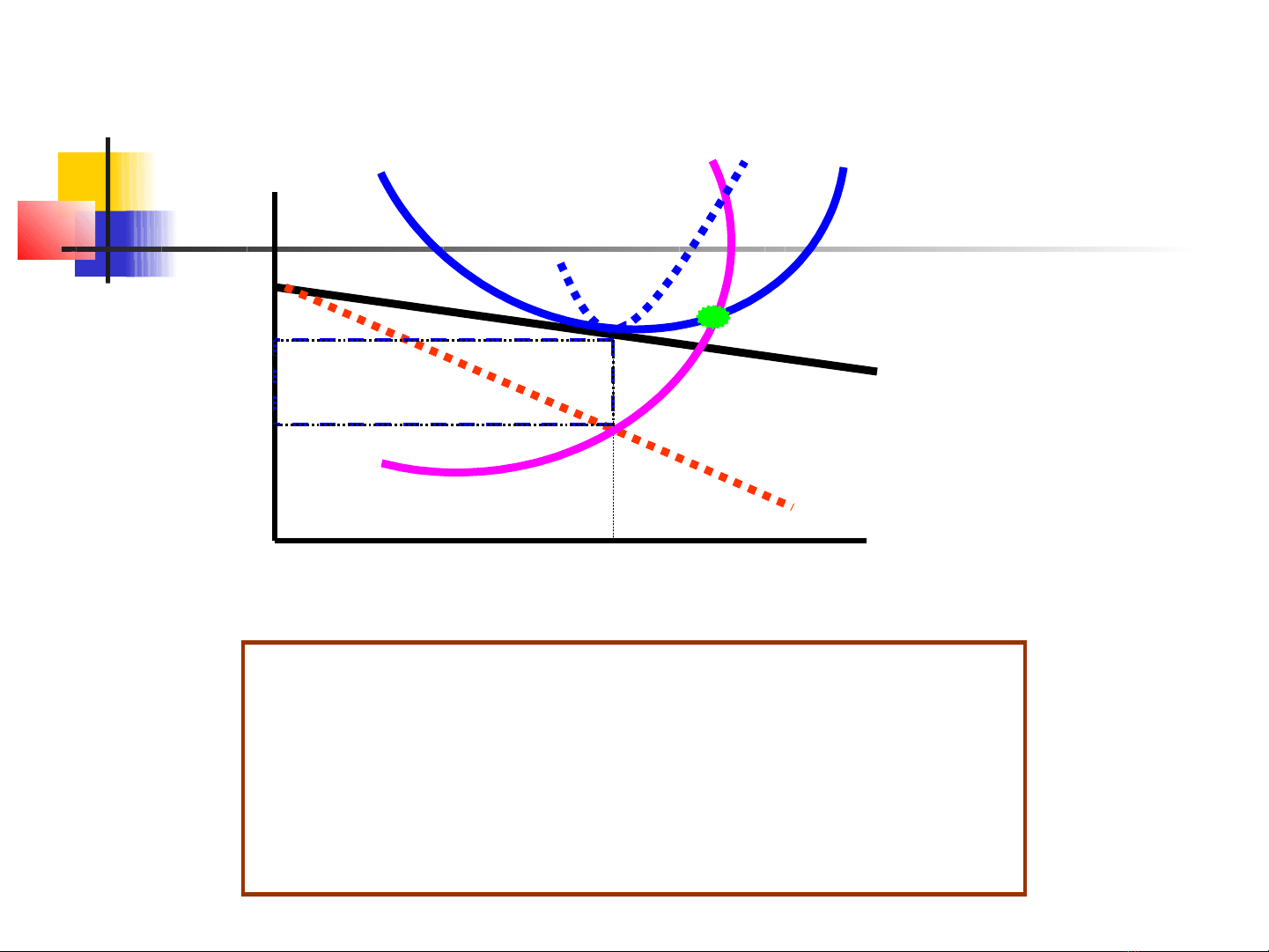
3. Cân b ng dài h n c a DNằ ạ ủ
Q
P
AR= d
MR
P*
C
Q*
B
LAC
LMC
Đ.Ki n: cân b ng dài h n:ệ ằ ạ
P* = LAC = SAC (khác LACmin)
MR = LMC = SMC
SAC
LACmin
5
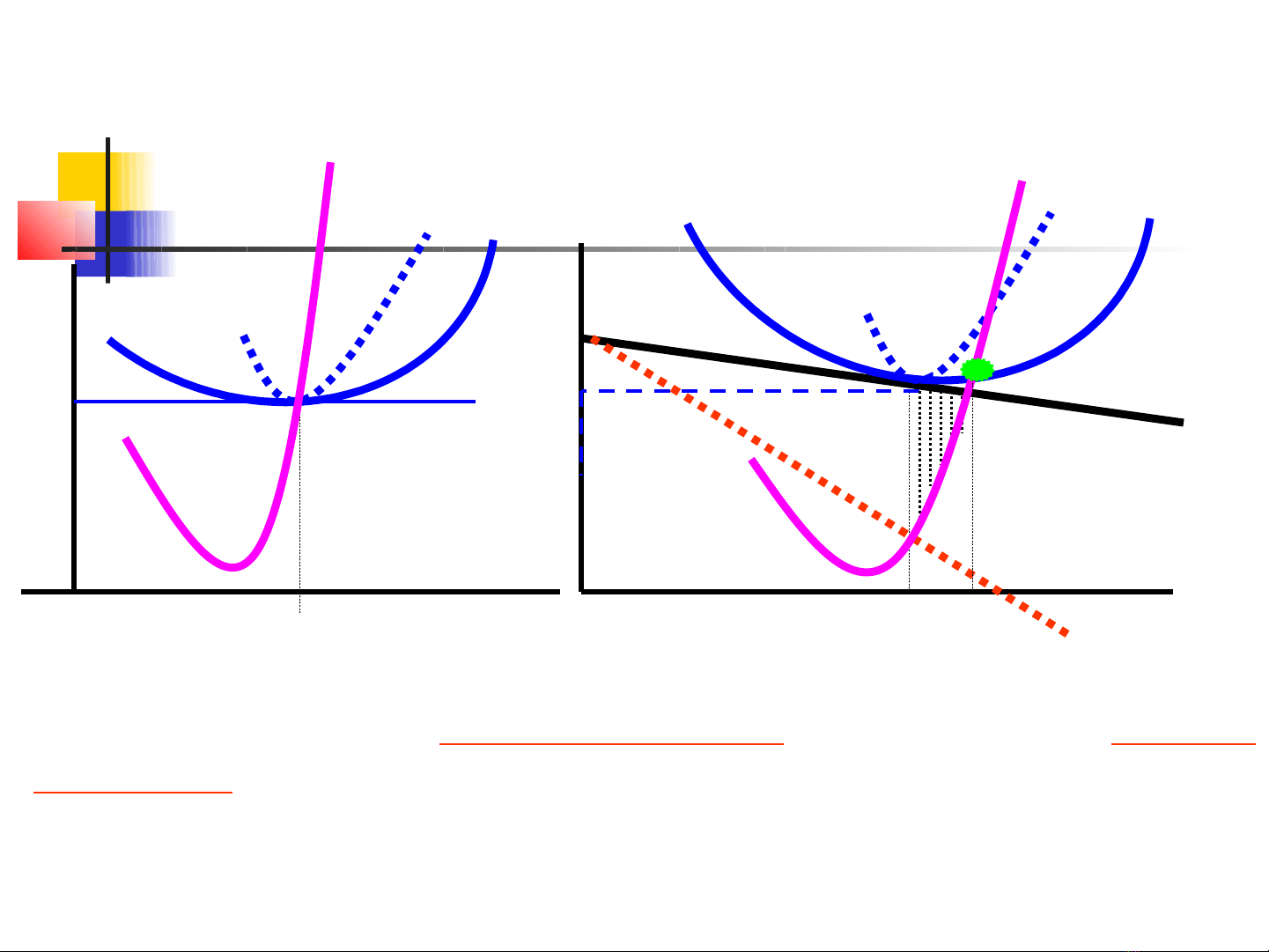
c. Hi u qu kinh tệ ả ế
Q
P
AR= d
MR
P*
Q* <
LAC
LMC
SAC
DWL
Q
P
P*
Q*
SAC LAC
LMC
P = MC = MR =LACmin
TT c nh tranh hoàn h oạ ả TT c nh tranh ĐQạ
*. P và CF trung bình: P = LAC > LMC
**. P và SL: Vì SX v i ớQMSX < QMSX t i uố ư Pbán > MC. Nên có P cao h n ơ
và Q nh h nỏ ơ TT c nh tranh hoàn h o. ạ ả DWL = ABC
***. Kh năng d th a sp là r t nh (do Eả ư ừ ấ ỏ d co giãn nhi u).ề
***. SP đa d ng thích h p v i t ng nhóm khách hàngạ ợ ớ ừ
Qhoàn h oả
LACmin