1
TRƯỜNG ĐẠI HỌC SƯ PHẠM – ĐẠI HỌC HUẾ
KHOA TOÁN
--------
Sinh viên thực hiện: Trần Mỹ Kỳ Duyên
MÔN HỌC: ĐÁNH GIÁ
TRONG GIÁO DỤC TOÁN
Giảng viên hướng dẫn: Nguyễn Đăng Minh Phúc
Lớp: Toán 4T
Huế, tháng 04 năm 2017
2
§2. CÁCH VIẾT CÂU HỎI TRẮC NGHIỆM
KHÁCH QUAN
ĐỀ TÀI. BÀI TOÁN THỰC TẾ LIÊN QUAN ĐẾN CÁC MẶT TRÒN XOAY
Câu 1. Một lọ nước hoa thương hiệu Chloé được thiết kế như sau: vỏ là dạng hình nón
có đỉnh 𝑆 và đáy là hình tròn tâm 𝑂, bán kính 𝑅, chiều cao của hình nón là ℎ; phần
chứa dung dịch nước hoa lại là hình trụ nội tiếp hình nón trên. Hỏi các nhà thiết kế
nên thiết kế như thế nào để vỏ nước hoa vẫn là hình nón như trên mà lọ nước hoa có
thể chứa được nhiều dung dịch nước hoa nhất?
Giải.
Giả sử ta có hình trụ nội tiếp hình nón như hình vẽ.
Đặt 𝑂𝐻 =𝑥 là chiều cao của hình trụ (0 < 𝑥<ℎ)
Gọi 𝑟 là bán kính đường tròn đáy của hình trụ, 𝑉 là thể tích khối trụ.
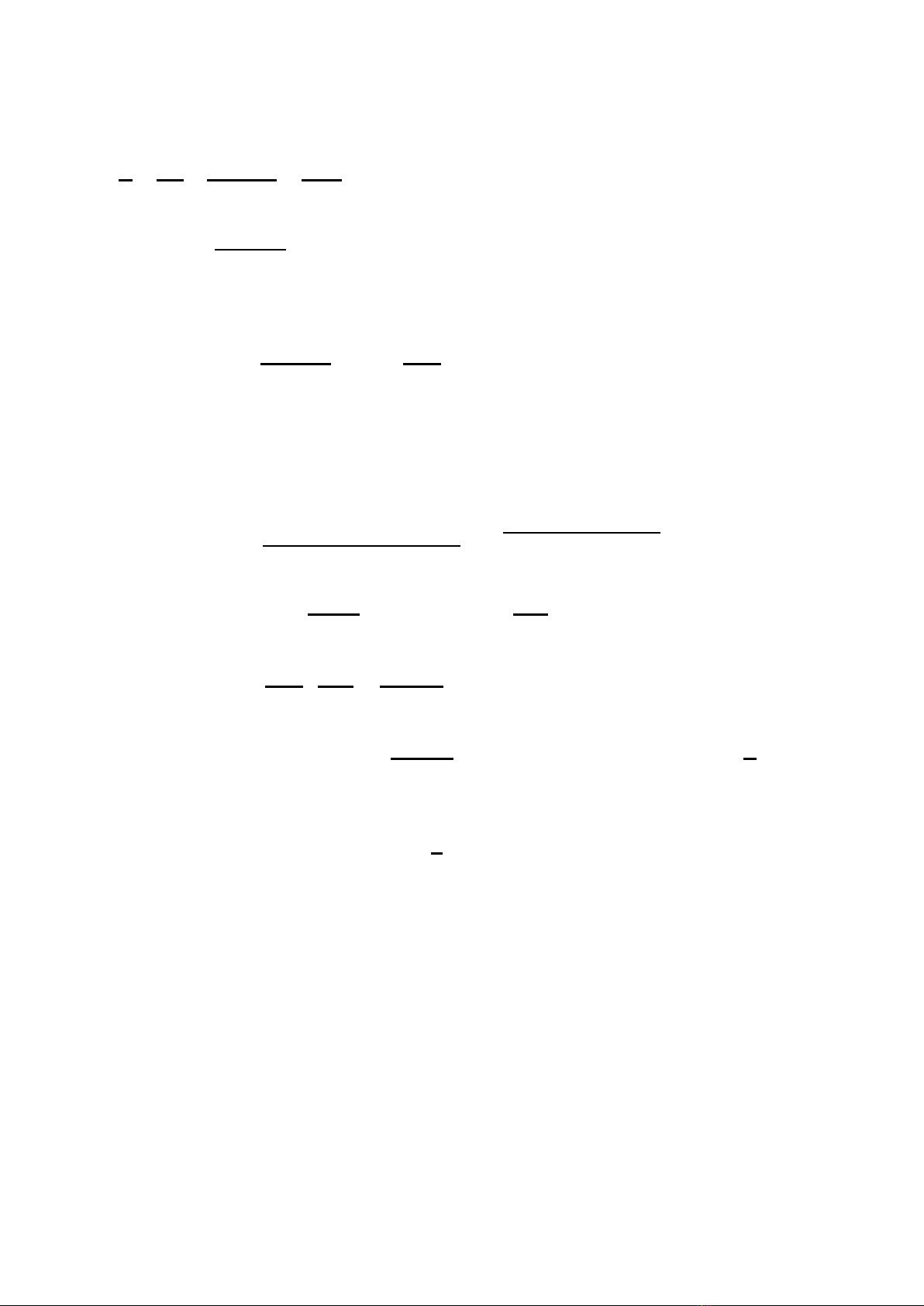
3
Xét tam giác 𝑆𝑂𝐴 vuông tại 𝑂, ta có:
𝑟
𝑅 = 𝑆𝐻
𝑆𝑂 = 𝑆𝑂−𝑂𝐻
𝑆𝑂 = ℎ−𝑥
ℎ
Suy ra: 𝑟= 𝑅(ℎ−𝑥)
ℎ
Thể tích của khối trụ được tính bởi công thức
𝑉= 𝜋𝑟2ℎ′=𝜋 (𝑅(ℎ−𝑥)
ℎ)2. 𝑥= 𝜋𝑅2
ℎ2 (ℎ − 𝑥)2.𝑥
Đưa bài toán đã cho trở thành bài toán: Tìm mối liên hệ giữa ℎ và 𝑥 để thể tích khối
trụ là lớn nhất?
Áp dụng bất đẳng thức Cauchy cho ba số không âm ℎ − 𝑥,ℎ − 𝑥, 2𝑥 ta có:
ℎ − 𝑥 + ℎ − 𝑥 + 2𝑥
3≥ ℎ − 𝑥 ℎ − 𝑥 . 2𝑥
3
Suy ra: (ℎ − 𝑥)2. 2𝑥 ≤ (2ℎ)3
27 ⟹(ℎ − 𝑥)2.𝑥 ≤ 4ℎ3
27
Do đó, ta có: 𝑉 ≤ 𝜋𝑅2
ℎ2.4ℎ3
27 = 4𝜋𝑅2ℎ
27
Vậy 𝑉 đạt giá trị lớn nhất là bằng 4𝜋𝑅2ℎ
27 khi và chỉ khi ℎ − 𝑥 = 2𝑥 ⟺ 𝑥 = ℎ
3.
Vậy các nhà thiết kế phải thiết kế hình trụ nội tiếp hình nón đã cho với tỉ lệ chiều cao
hình trụ và chiều cao hình nón là bằng 1
3.
Phân tích
Nhiệm vụ đầu tiên của học sinh là sử dụng các thông tin mà bài toán cho để
thành lập một mô hình toán. Bước này liên quan đến khả năng tưởng tượng của các
em học sinh, liên quan đến kiến thức cũng như hiểu biết của các em về hình dạng của
hình nón, hình trụ cũng như hình trụ nội tiếp hình nón. Ở bước này tối thiểu các em
phải tưởng tượng được hình dạng mô hình toán mà bài toán đặt ra. Giả sử rằng học
sinh có đủ kiến thức và khả năng này thì em đó sẽ vẽ một mô hình như sau.
4
Sau đó, học sinh phải nhận ra rằng em phải đưa bài toán đã cho về bài toán liên
quan đến các mặt tròn xoay, cụ thể ở đây là chỉ ra được hình trụ nội tiếp hình nón có
đỉnh 𝑆 và đáy là hình tròn tâm 𝑂, bán kính 𝑅, chiều cao của hình nón là ℎ sao cho khối
trụ có thể tích lớn nhất.
Học sinh phải nhận ra rằng em phải có những thông tin nào để tính thể tích của
khối trụ và so sánh xem đề bài đã cho những gì. Nếu đề bài không cho thì chúng ta
phải biết đặt ẩn phụ rồi tìm các mối liên hệ với các thông tin đề bài đã cho. Rồi học
sinh phải gọi ra được công thức tính thể tích khối trụ là: 𝑉= 𝜋𝑟2ℎ với ℎ là chiều cao
của hình trụ, 𝑟 là bán kính đường tròn đáy của hình trụ.
Học sinh biến đổi công thức này về dạng thích hợp, cố gắng biến đổi để tất cả
đều được biểu diễn theo các thông tin mà đề đã cho và cuối cùng là tiến hành làm bài
toán bất đẳng thức: tìm giá trị lớn nhất của biểu thức 𝑉. Ở đó khả năng giải các bài
toán liên quan đến bất đẳng thức của học sinh sẽ được bộc lộ, mà cụ thể là kĩ thuật
biến đổi tương đương, kĩ thuật phân tích hằng đẳng thức, kĩ thuật thêm bớt hằng số,…
Những câu hỏi trắc nghiệm khách quan tương đương
Giả sử những bước cơ bản đầu tiên học sinh đều đã thực hiện được, những bước
đầu tiên chỉ kiểm tra được khả năng tương tượng cũng như đọc hiểu đề của học sinh.
Đồng thời cũng kiểm tra khả năng thể hiện câu hỏi bằng lời thành hình vẽ.
Tiếp theo, bài toán kiểm tra khả năng nhớ của học sinh về công thức tính thể tích
của các mặt tròn xoay, cụ thể là thể tích của khối trụ. Ta có thể xây dựng một câu hỏi
trắc nghiệm để kiểm tra khả năng đó như sau:
5
Ví dụ 1. Cho hình trụ có hai đáy là hai đường tròn (𝑂,𝑅) và (𝑂′,𝑅), hình trụ có chiều
cao là ℎ. Gọi 𝑉 là thể tích của khối trụ đã cho. Hãy viết công thức tính 𝑉?
A. 𝑉= 2𝜋𝑅ℎ B. 𝑉=𝜋𝑅ℎ
C. 𝑉=𝜋𝑅2ℎ D. 𝑉= 1
3 𝜋𝑅2ℎ
Câu hỏi này chỉ ở mức độ nhận biết, với câu hỏi này học sinh chỉ cần nhớ kiến
thức liên quan đến thể tích của khối trụ thì có thể dễ dàng chọn được đáp án
chính xác là đáp án C. Tuy nhiên vẫn sẽ có học sinh chọn các phương án nhiễu,
đặc biệt là phương án D, vì khi nhắc đến thể tích các em thường hay làm là
𝑉= 1
3 𝑆đá𝑦.ℎ.
Bước tiếp theo của bài toán là khả năng giải quyết các bài toán liên quan đến
hình học phẳng, cụ thể là giải bài toán trong tam giác 𝑆𝑂𝐴 vuông tại 𝑂. Tương tự, ở
đây ta cũng có thể viết những câu hỏi trắc nghiệm khách quan liên quan đến khía cạnh
này để kiểm tra khả năng đó của học sinh.
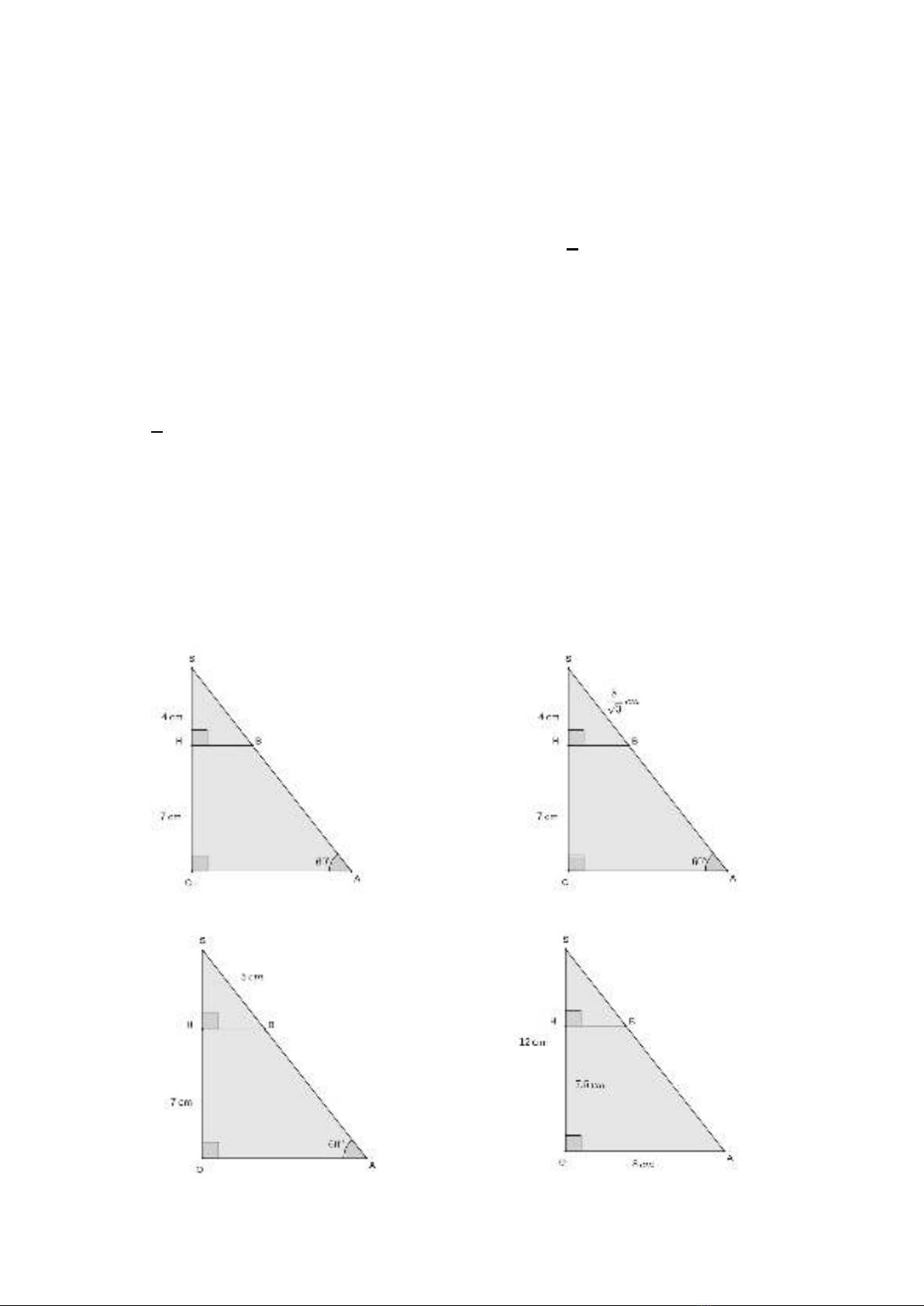
Ví dụ 2. Cho các tam giác I, II, III, IV sau đây:
(I) (II)
(III) (IV)