
1
MỘT SỐ DẤU HIỆU CHẨN ĐOÁN CHẤT LƯỢNG Ổ BI
Nguyễn Cao Mệnh và Vũ Thanh Trúc
(Viện Cơ học Ứng dụng)
T óm t ắt
Ảnh hưởng của chất lượng ổ bi đến động lực học của
hệ Rôto-Gối đỡ ổ bi (hệ R-G) là vấn đề khá phức tạp.
Tuy nhiên bằng cách phân tích sự làm việc của ổ bi
khi chịu tải, mô phỏng động lực học hệ R-G ta có thể
nhận được những đặc điểm khác nhau về dao động
của hệ này khi ổ bi có các loại khuyết tật khác nhau.
Các đặc điểm này chính là các dấu hiệu để khi đo và
phân tích tín hiệu dao động của hệ R-G ta có thể
đánh giá được chất lượng của ổ bi và nhận dạng loại
khuyết tật đang tồn tại. Việc chẩn đoán chính xác
chất lượng của ổ bi là một trong những cơ sở cho
việc bảo dưỡng thiết bị theo trạng thái, một phương
pháp bảo dưỡng được đánh giá là kinh tế hiện nay.
SOME SYMPTOMS FOR DIAGNOSING
QUALITY OF BALL-BEARINGS
The effect of ball-bearings quality on dynamics of
rotor-bearing system is rather complicated. However,
on the basis of analysing behaviour of ball-bearing
under loading, and by simulating dynamics of rotor-
bearing system it is able to receive the different
characteristics of this system vibration with respect to
different defects of ball-bearing. These
characteristics are the very symptoms for identifying
defects of ball-bearing and estimating its quality by
measurement and analysis of the system vibration.
The exact diagnosis of ball-bearing quality is the
basis for condition based maiternance of machines,
one mainternance technique advantaged now for
economics.
§1. Mở đầu
Một thiết bị có bộ phận quay (rotor) và gối đỡ
có bạc ổ bi (hệ R-G), thì rung động thường gây ra do
lệch tâm và chất lượng của ổ bi. Mức độ khuyết tật
của ổ bi ảnh hưởng đến dao động của toàn hệ. Mặt
khác, dù cho rôto có được cân bằng tốt đến mấy vẫn
còn lệch tâm ở mức độ cho phép nên vẫn gây ra dao
động nhỏ, còn khuyết tật của ổ bi ngày càng tăng do
quá trình vận hành và phải thay thế theo việc đánh giá
chất lượng hoặc đến kỳ bảo dưỡng. Tuy nhiên, một
trong những nguyên nhân phải dừng máy đột ngột là
do chất lượng của ổ bi trong quá trình vận hành. Vì
vậy, việc đánh giá trạng thái chất lượng và khuyết tật
của ổ bi trong quá trình vận hành bằng phương pháp
đo và phân tích rung động của hệ R-G sẽ đem lại lợi
ích trong thực tế và phục vụ cho việc bảo dưỡng theo
trạng thái kỹ thuật của máy. Để thực hiện được mục
đích đó, ta cần biết ảnh hưởng của các loại khuyết tật
của ổ bi đến rung động của toàn hệ như thế nào. Nói
cách khác, mỗi loại khuyết tật làm cho rung động của
toàn hệ có đặc điểm gì? Do đó cần phải mô hình hoá
hệ dao động, mô phỏng các loại lực sinh ra ứng với
các loại khuyết tật của ổ bi cùng tồn tại với lực ly tâm
vốn có của bộ phận quay không thể tuyệt đối cân
bằng, rút ra các dạng dao động có thể đo được của
toàn hệ cùng với các đặc tính của chúng. Từ việc mô
phỏng trên, ta có thể lấy các đặc điểm rung động làm
cơ sở cho việc nhận dạng khuyết tật của ổ bi từ kết
quả đo và phân tích rung động của hệ R-G.
§ 2. Đánh giá độ cứng và phân tích chuyển động
quay của ổ bi.
Trong phần này sẽ giới thiệu một số kết quả của
các tài liệu [1,2,3] để sử dụng trong các phần sau. Để
lập mô hình toán học của chuyển động hệ rôto- gối đỡ
loại ổ bi ( hệ R-G), ta cần phải đánh giá độ cứng của
ổ bi, phân tích chuyển động quay của các phần tử
trong ổ bi sẽ liên quan đến tần số kích động của ngoại
lực.
a) Đánh giá độ cứng của ổ bi:
Trước hết dựa vào phân tích biến dạng của ổ bi theo
[1,2] ta có:
2
3
0
2
1
2
3
)()2.1( xxdNFFF ds +
=+= − (2.1)
trong đó N- số viên bi
d- đường kính của viên bi
Fs- tải trọng tĩnh
Fd- tải trọng động
x- biến dạng động
xo- biến dạng tĩnh của ổ bi khi chịu tải tĩnh
Fs, tức là
2
3
0
2
1
2
3
)2.1( xdNFs
=− (2.2)
Từ (2.1) ta có thể biến đổi như sau:
2
3
2
3
2
3
0
2
1
2
3
)1()1()2.1( uFuxdNFFF sds +=+
=+= −
(2.3)
trong đó u = x/xo
Khai triển (2.3) theo u ta sẽ có:
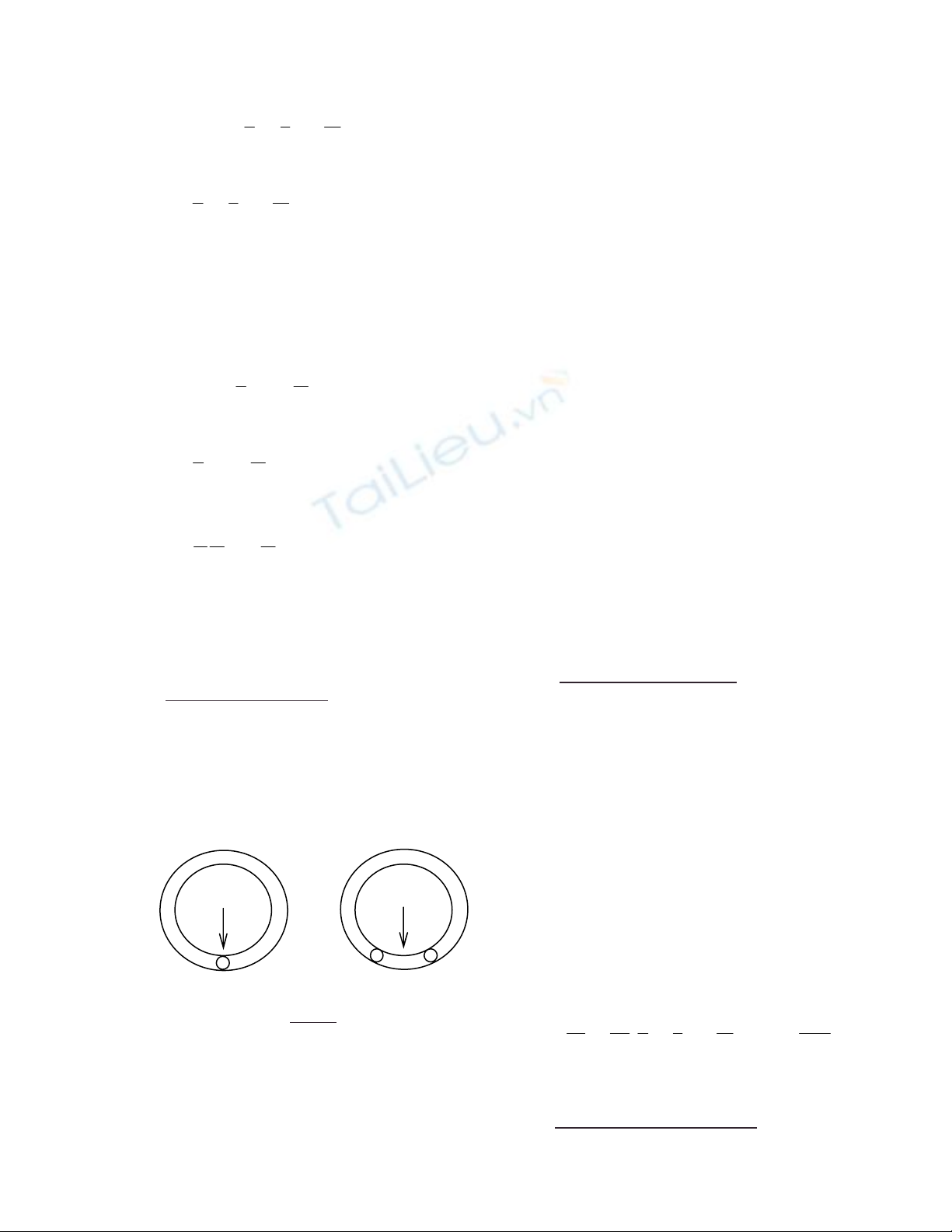
2
...)
16
1
8
3
2
3
1( 32 +−++=+ uuuFFF sds (2.4)
Do đó,
...)
16
1
8
3
2
3
(32 +−+= uuuFF sd (2.5)
b) Phân tích chuyển động quay của ổ bi.
Theo [1,3], trong trường hợp vành trong của ổ bi
quay cùng với trục với tần số f, còn vành ngoài đứng
yên, ta có
- Tần số tiếp xúc fi của một điểm trên vành trong
với ổ bi N viên là
)cos1(
2
1
α
D
d
fNfi+= (2.6)
- Tần số tiếp xúc fe của một điểm trên vành ngoài
với ổ bi N viên là
)cos1(
2
1
α
D
d
fNfe−= (2.7)
- Tần số tiếp xúc fb của một điểm trên một viên bi
với vành trong hoặc vành ngoài là
−=
α
2
2cos1
2D
d
d
Df
fb (2.8)
trong đó d- đường kính của viên bi
D- đường kính của vòng tròn đi qua tâm các viên bi.
α
- là góc tiếp xúc của viên bi với vành trong và
vành ngoài.
§ 3. Các lực tác động lên ổ bi
Đối với hệ R-G, lực tác động lên gối đỡ ổ bi trước
hết là tải tĩnh, chính là trọng lượng của Rô-to và trục.
Tải trọng động bao gồm lực ly tâm quán tính do khối
lượng mất cân bằng m gây ra. Nếu xét dao động của
hệ theo phương thẳng đứng thì lực này có dạng:
)2sin()2( 2ftfmrFl
ππ
= (3.1)
Trong quá trình trục quay, các viên bi chuyển động
không phải lúc nào cũng có một viên bi ở vị trí như
trên Hình 1a, do đó độ cứng của ổ bi theo hướng
thẳng đứng thay đổi với tần số theo công thức (2.7),
làm cho trục dao động theo dưới tác dụng của tải
trọng tĩnh theo chiều thẳng đứng với tần số trên và
sinhralực quán tính tác động lên hệ bằng khối lượng
của Roto nhân vớI gia tốc chuyển động .Lực quán
tính này sẽ là
)2sin()2( 2tffMaFeeq
ππ
= (3.2)
Trong công thức (3.2) M là khối lượng của rôto và
trục quay, a- biên độ dao động của trục trong ổ bi, do
độ cứng không đều của ổ bi sinh ra, và được giả thiết
có dạng )2sin( tfa e
π
.
Khi ổ bi có một điểm khuyết tật ở vành trong, sẽ
sinh ra lực va chạm mỗi khi có một viên bi đi qua
điểm khuyết tật ấy, và do đó va chạm sẽ có dạng:
∑
∞
=
−=
1
111 )(
i
iv iTtHF
δ
(3.3)
trong đó Fv1 là ký hiệu lực va chạm do một điểm
khuyết tật ở vành trong, H1i là biên độ va chạm,
δ
là
hàm Dirac, T1 là chu kỳ va chạm, T1=(fi)-1, fi được
cho trong công thức (2.6).
Tương tự như vậy, nếu có khuyết tật ở vành ngoài, ta
có công thức cho lực va chạm , và ở đây ta dùng chỉ
số 2 thay cho số 1 trong (3.3).
∑
∞
=
−=
1
222 )(
i
iv iTtHF
δ
(3.4)
trong đó T2=(fe)-1, fe được cho bởi công thức (2.7).
Nếu một viên bi bị mẻ, thì lực va chạm sinh ra có
chu kỳ T3=(fb)-1, và ta có:
()
∑
∞
=
−=
1
333
i
iv iTtHF
δ
(3.5)
§ 4. Phương trình chuyển động
Tuỳ theo phương pháp đo dao động để phân tích
và so sánh với kết quả mô phỏng, ta sẽ xây dựng mô
hình toán học mô tả chuyển động của hệ khác nhau.
Giả sử, ta dùng đầu đo không tiếp xúc (proximity
probe) để đánh giá dao động tương đối của trục đối
với gối đỡ và trong hệ R-G, đó là rotor cứng, thì ta
chỉ quan tâm đến độ cứng và hệ số cản của ổ bi, và
ta có hệ dao động 1 bậc tự do dưới dạng:
)()(2 tFxFxhxM d=++ &&& (4.1)
trong đó M- khối lượng của rotor và trục quay, h- hệ
số cản nhớt, Fd(x)- lực đàn hồi, còn F(t) - ngoại lực
bao gồm các lực (3.1)-(3.5) ở trên.
Chia 2 vế của phương trình (4.1) cho Mxo và ký hiệu
u=x/xo, ta có:
)(
1
...)
16
1
8
3
2
3
(2 32 tF
Mx
uuu
x
g
u
M
h
u
oo
=+−+++ &&&
(4.2)
§ 5. Kết quả tính toán và nhận xét
b)
H
ình 1

3
1. Để áp dụng những kết quả đã thu được trong
những phần trên, ta nghiên cứu dao động của hệ
R-G với bạc ổ bi 36309 có các tham số sau:
- Khối lượng của rô to và trục là M=2000 kg.
- Khối lượng lệch tâm là m=0.05kg (để thấy rõ
tác dụng của lực ly tâm ta xét cả trường hợp
m=0.5 kg).
- Bán kính lệch tâm r=0.5m.
- Số viên bi trong ổ đỡ N=12
- Đường kính viên bi d=17.46mm.
- Đường kính vòng tròn qua tâm các viên bi
D=72.5mm.
- Rô to quay với tốc độ 1500v/ph, tương ứng với
tần số f=25Hz.
Áp dụng các công thức của phần trên ta tính được:
+ Dịch chuyển tĩnh của trục xo=64.1965
m
µ
+ Tần số riêng fn=76.119 Hz
+ Các tần số va chạm sinh ra do khuyết tật là:
fi=148.8 Hz, fe=91.2 Hz , fb=39.11
2. Các lực va chạm (3.3)-(3.5), được biểu diễn qua
hàm Dirac. Trong tính toán bằng số ta khai triển
các hàm này thành chuỗi Fourier và nhận được
dạng sau [5]:
∑
∞
=
+=
1
111 )2sin(42
j
iiiv tjfHfHfF
πππ
(5.1)
)2sin(42 2
1
22 tjfHfHfF ee
j
ev
πππ
∑
∞
=
+= (5.2)
)2sin(42 3
1
33 tjfHfHfF bb
j
bv
πππ
∑
∞
=
+= (5.3)
Trong các công thức trên, H1, H2, H3 là các hằng số
thể hiện cường độ va chạm. Để chẩn đoán khuyết tật
của ổ bi, ta dùng các dấu hiệu tần số là chính, nên có
thể cho các hằng số này một số giá trị nào đó trong
tính toán.
Trong các công thức (5.1)-(5.3), từ giá trị các tần số
ta sẽ lấy một số hữu hạn các số hạng trong các tổng
trên, cụ thể là, trong (5.1) ta lấy 1 số hạng, trong
(5.2) ta lấy 2 số hạng, còn trong (5.3) ta lấy 3 số
hạng.
3. Bây giờ ta xét các trường hợp riêng để tìm ra
các dấu hiệu chẩn đoán.
3.1 Hệ R-G chỉ có lực ly tâm do mất cân bằng
sinh ra, với m=0.05kg (Hình 2).
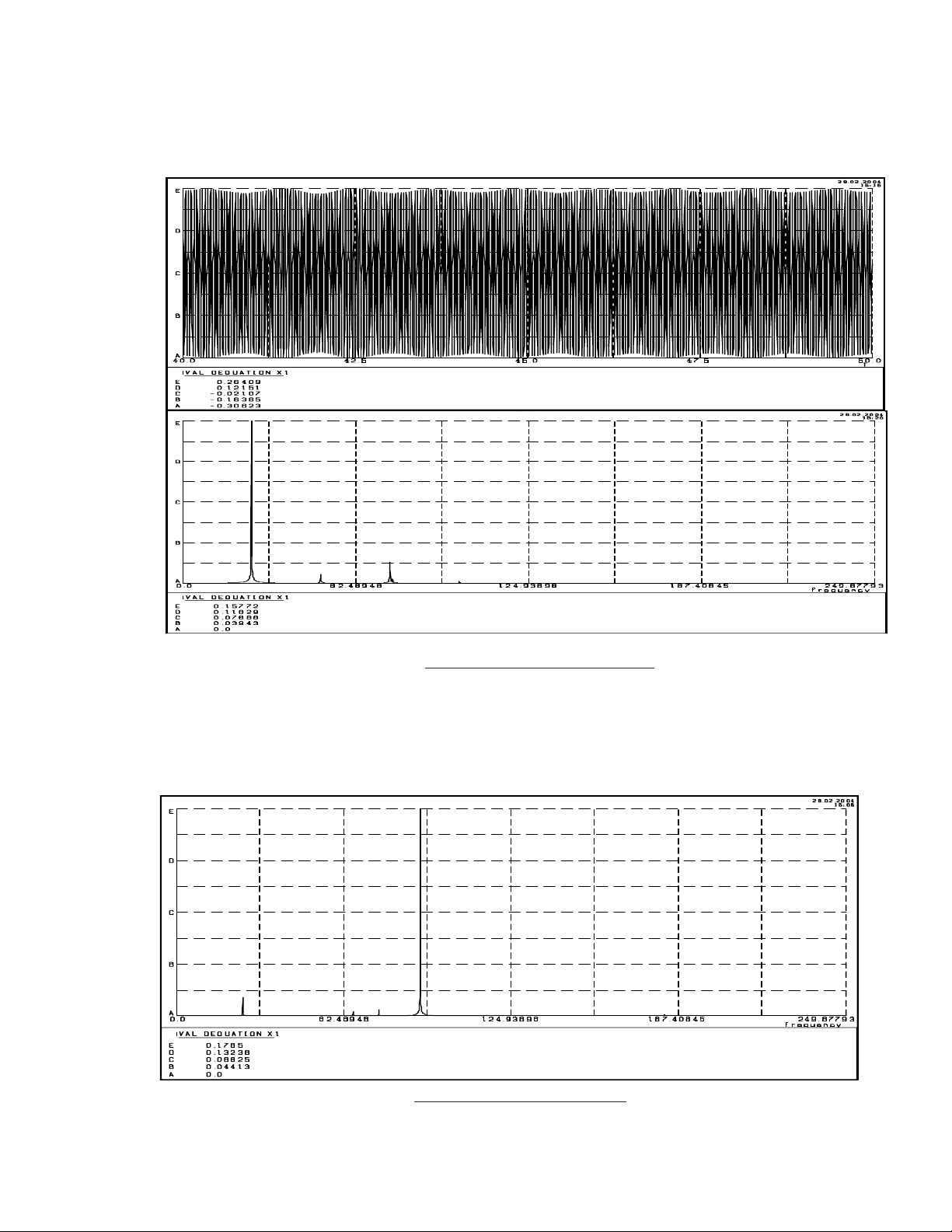
Nhận xét: Trong trường hợp này, trong đồ thị
phổ nổi lên 2 đỉnh, đỉnh cao ứng với tần số kích
động 25 Hz, đỉnh thấp ứng với tần số riêng
96.198 Hz.Không thể hiện ảnh hưởng của thành
phần phi tuyến.
Hình 2 Dao động và phổ trong trường hợp 3.1
4
3.2 Hệ R-G chỉ có lực ly tâm lớn hơn với
m=0.5kg ta có đồ thị dao động và phổ
(Hình 3)
Nhận xét: Khi tăng lực kích động, trong đồ thị
phổ xuất hiện đỉnh mới là tần số phân hài của
tần số riêng fn , do tác dụng của hệ số phi tuyến.
Hình 3. Dao động và phổ cho trường hợp 3.2
3.3 Trường hợp tồn tại cả lực ly tâm nhỏ
(m=0.05) và lực quán tính của trục ta có đồ
thị phổ dao động (Hình 4).
Nhận xét: Khi đó tần số lực quán tính chiếm ưu
thế, thể hiện trên đồ thị phổ hình 4, vì tần số này
gần với tần số riêng hơn.
Hình 4. Phổ dao động cho trường hợp 3.3
5
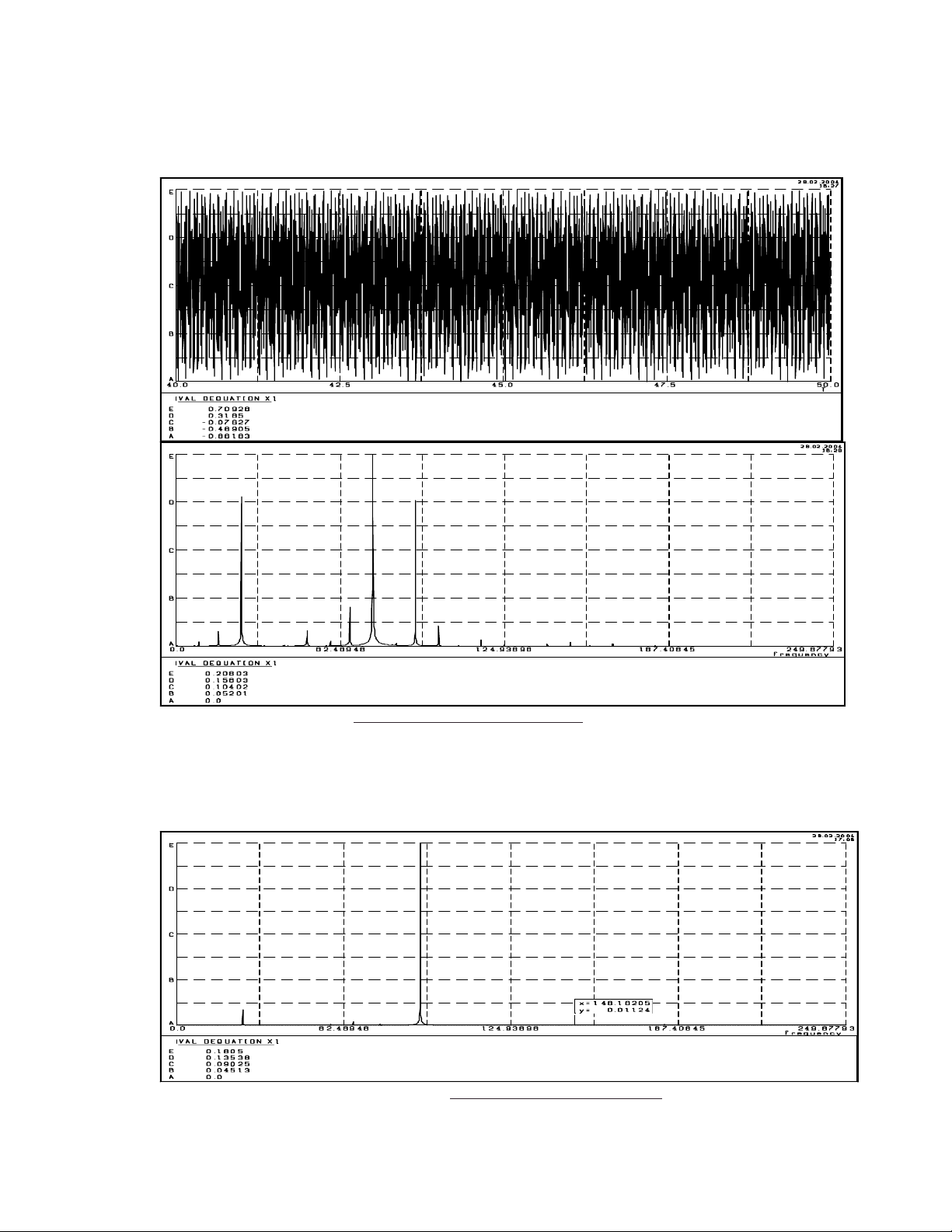
3.4 Hệ R-G có lực ly tâm lớn (m=0.5) và lực
quán tính của trục (Hình 5). Nhận xét: Khi đó xuất hiện trong biểu diễn phổ
nhiều dao động phân hài của tần số riêng fn và
bội của tần số quay f.
Hình 5. Dao động và phổ cho trường hợp 3.4
3.5 Hệ R-G có các lực Fl , Fq và Fv1 với các tần
số f, fe, fi (Hình 6). Đồ thị phổ trên hình vẽ
cho ta nhận xét sau.
Nhận xét: Trong trường hợp này, các tần số f, fe
và fi đều thể hiện trên đồ thị phổ, nhưng tần số fe
thể hiện trội hơn vì gần với tần số riêng hơn.
Hình 6. Phổ dao động cho trường hợp 3.5












![Đề cương đề tài nghiên cứu khoa học [chuẩn nhất/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251117/duong297/135x160/26111763433948.jpg)













