Đề kiểm tra HK2 Toán 11 - THPT Cao Lãnh 1 (2012-2013) - Kèm đáp án

Chia sẻ: Huynh Hoa Lan | Ngày: | Loại File: DOC | Số trang:4

Thêm vào BST

Báo xấu

167
lượt xem 23
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Tham khảo đề kiểm tra học kỳ 2 môn Toán lớp 11 của trường THPT Cao Lãnh 1 giúp cho các bạn học sinh lớp 11 có thêm tài liệu ôn tập, chuẩn bị cho kỳ thi sắp tới.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Đề kiểm tra HK2 Toán 11 - THPT Cao Lãnh 1 (2012-2013) - Kèm đáp án

SỞ GD & ĐT ĐỒNG THÁP TRƯỜNG THPT CAO LÃNH 1 ĐỀ KIỂM TRA HỌC KỲ 2 – TOÁN 11 (tham khảo) Thời gian: 90 phút Năm học: 2012 – 2013 I. PHẦN CHUNG CHO TẤT CẢ CÁC HỌC SINH (8,0 điểm) Câu I (3,0 điểm) ( ) 1) Tìm các giới hạn sau: 2 x 2 − 3x + 1 a) lim n 2 +2n − n b) lim 3 − x x → −∞ 2) Xét tính liên tục của hàm số sau tại điểm x0 = - 2:  3x 3 − 4 x + 16  khi x ≠ −2 f ( x) =  x+2 4 x 2 − 5 x + 6 khi x = −2  Câu II (2,0 điểm) 1) Cho hàm số y = x. cosx. Chứng minh y + y’’ + 2sinx = 0 1 3 4 2) Cho hàm số f ( x ) = x − 2 x + 3 x − . Giải bất phương trình: f ' ( x) ≤ 0 . 2 3 3 Câu III (3,0 điểm) Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân ở A, SB ⊥ (ABC) và SB = AB = 2a. 1)Chứng minh rằng các mặt bên của hình chóp là những tam giác vuông. 2)Tính góc hợp bởi hai mặt phẳng (SAC) và (ABC). 3)Gọi I là trung điểm của đoạn thẳng BC. Tính khoảng cách từ I đ ến mặt ph ẳng (SAC). II. PHẦN RIÊNG – PHẦN TỰ CHỌN (2,0 điểm) A. PHẦN 1 (THEO CHƯƠNG TRÌNH CHUẨN) Câu IVa ( 2,0 điểm) 1) Chứng minh rằng phương trình: 3x4 – 4x3 + 5x2 – 6 = 0 có ít nhất 2 nghiệm. 2) Cho hàm số y = x4 – 3x2 + 4 có đồ thị (C). Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ bằng - 1. B. PHẦN 2 (THEO CHƯƠNG TRÌNH NÂNG CAO) Câu IVb (2,0 điểm) 1) Chứng minh rằng phương trình sinx + cosx = x có ít nhất một nghiệm. 2x 2) Cho hàm số y = có đồ thị (C). Viết phương trình tiếp tuyến của (C) tại 2− x điểm có tung độ bằng 2 -------------------------Hết--------------------------
ĐÁP ÁN Câu Đáp án Thang điểm I 1a ( lim n + 2n − n 2 ) = lim n 2 + 2n − n 2 n 2 + 2n + n 0.25 2n  lim 2  = n 1 + + 1  n  0.25   2 = lim 1 + 2 + 1 0.25 n =1 0.25 1b x 2 (2 − 3 1 + ) 2 x − 3x + 1 2 x x2 0.25 lim 3− x = lim 3 x → −∞ x → −∞ x( − 1) x  3 1  2− + 2  = lim x. 3x x  x → −∞  −1  0.25    x  = +∞ 0.25 lim x = −∞  x → −∞   3 1 Vì:  2− + 2 lim x x = −2 0.25  x → −∞ 3 −1   x 2 f ( −2) = 32 (1) 0.25 ( x + 2)(3 x − 6 x + 8) 2 lim f ( x) = lim x → ( −2 ) x → ( −2 ) x+2 0.25 = lim (3x 2 − 6 x + 8) = 32 (2) 0.25 x → ( −2 ) Từ (1),(2) ta có lim f ( x) = f (−2) ⇒ Hàm số liên tục tại x0 = - 2. x → ( −2 ) 0.25 II y’ = cosx – x.sinx 0.25 1 y’’ = - sinx – (sinx + x.cosx) 0.25 = - 2sinx – x.cosx 0.25 Ta có: y + y’’ + 2sinx = x.cosx – 2sinx – x.cosx + 2sinx = 0 0.25 2 f ' ( x) = x2 – 4x + 3 0.5 f ' ( x) ≤ 0 ⇔ x 2 − 4 x + 3 ≤ 0 ⇔1≤ x ≤ 3 0.5 III
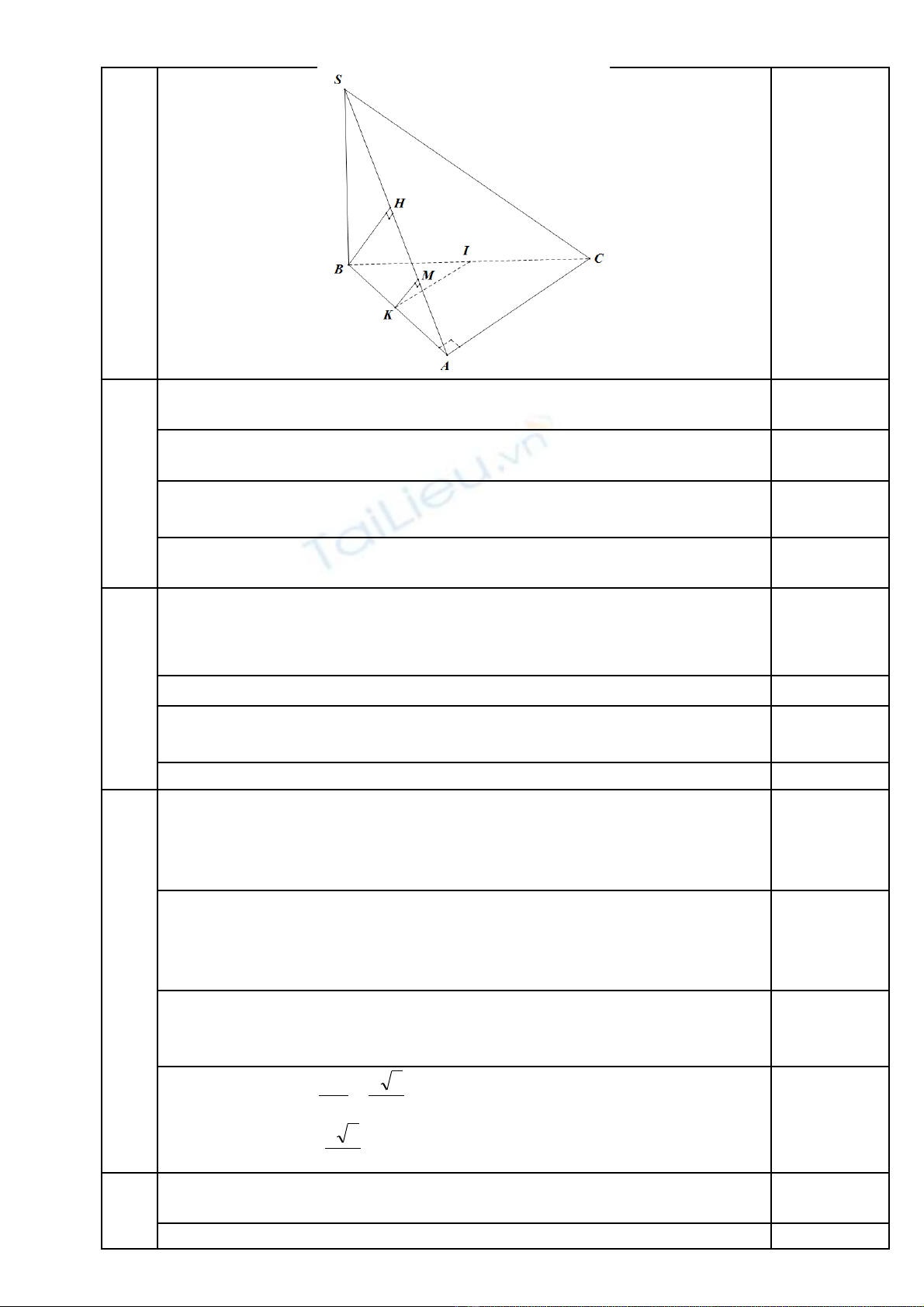
1) SB ⊥ (ABC) ⊃ BC ⇒ SB ⊥ BC ⇒ ∆SBC vuông ở B 0.25 SB ⊥ (ABC) ⊃ AB ⇒ SB ⊥ AB ⇒ ∆SAB vuông ở B 0.25 AC ⊥ AB   AC ⊥ SB  0.25 ⇒ AC ⊥ ( SAB) ⊃ SA ⇒ AC ⊥ SA ⇒ ∆SAC vuông ở A 0.25 2) ( SAC ) ∩ ( ABC ) = AC   AB ⊥ AC  SA ⊥ AC  0.25  ⇒ ( ( SAC ) , ( ABC ) ) = ( SA, AB ) = SAB ˆ 0.25 SA = AB = 2a   ⇒ ∆SAB vuông cân ở B ∆SAB vuông tai B (cmt ) 0.25 ˆ ⇒ SAB = 450 0.25 3) Trong ∆ vuông cân SAB. Kẻ đường cao BH ⊥ SA (H là trung điểm SA) 0.25 Do cmt AC ⊥ (SAB) ⊃ BH ⇒ AC ⊥ BH ⇒ BH ⊥ (SAC ) Gọi K là trung điểm của đoạn AB ⇒ IK // AC ⊂ (SAC ) ⇒ IK // (SAC ) 0.25 ⇒ d ( IK , ( SAC )) = d ( I , ( SAC )) = d ( K , ( SAC )) Trong tam giác vuông ABH. Kẻ KM // BH . Mà BH ⊥ (SAC ) . ⇒ KM ⊥ (SAC ) 0.25 ⇒ d ( K , ( SAC )) = KM BH a 2 = = 2 2 a 2 0.25 Vậy, d ( I , ( SAC )) = . 2 IVa Xét hàm số f (x) = 3x4 – 4x3 + 5x2 – 6 1) f (x) là hàm đa thức nên f (x) liên tục trên R 0.25 Ta có:
f (−1) = 6 f (0) = −6 f (2) = 30 0.25 Suy ra: f (−1). f (0) < 0 ⇒ phương trình f (x) = 0 có ít nhất 1 nghiệm ∈ (-1; 0) 0.25 f (0). f (2) < 0 ⇒ phương trình f (x ) = 0 có ít nhất 1 nghiệm ∈ (0; 2) Vậy: Phương trình f (x) = 0 có ít nhất 2 nghiệm trên R. 0.25 2) y’ = 4x3 – 6x 0.25 x0 = - 1 ⇒ y0 = 2 0.25 f ' ( x0 ) = f ' (−1) = 2 0.25 Phương trình tiếp tuyến của (C) tại điểm (-1; 2) là: y = 2x + 4 0.25 Ivb Xét hàm số f (x) = sinx + cosx – x liên tục trên R 1) 0.25 f (0) = 1 0.25 f (π ) = −1 − π 0.25 f (0). f (π ) < 0 ⇒ phương trình f (x) = 0 có ít nhất 1 nghiệm ∈ (0; π ) 0.25 2) y' = 4 ( 2 − x) 2 0.25 y0 = 2 ⇒ x0 = 1 0.25 f ' ( x0 ) = f ' (1) = 4 0.25 Phương trình tiếp tuyến của (C) tại điểm (1; 2) là: y = 4x - 2 0.25