TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT ĐỀ THI CUỐI KỲ HỌC KỲ I NĂM HỌC 18-19
THÀNH PHỐ HỒ CHÍ MINH Môn: PHƯƠNG PHÁP TÍNH
KHOA KHOA HỌC ỨNG DỤNG Mã môn học: MATH121101
BỘ MÔN TOÁN Đề thi số 101010 - Đề thi có 2 trang.
***** Thời gian 75 phút. Được phép sử dụng tài liệu
Câu 1. (2.5đ) Cho bài toán Cauchy:
(y0(x) = xy2+ 0.2
y(0) = 0.1
a. Áp dụng phương pháp Euler, h=0.1, tính gần đúng y(0.2) ≈(1), y(0.6) ≈(2). Từ đó suy ra
y0(0.2) ≈(3).
b. Áp dụng phương pháp Euler cải tiến, h=0.1, tính gần đúng y(0.2) ≈(4), y(0.5) ≈(5).
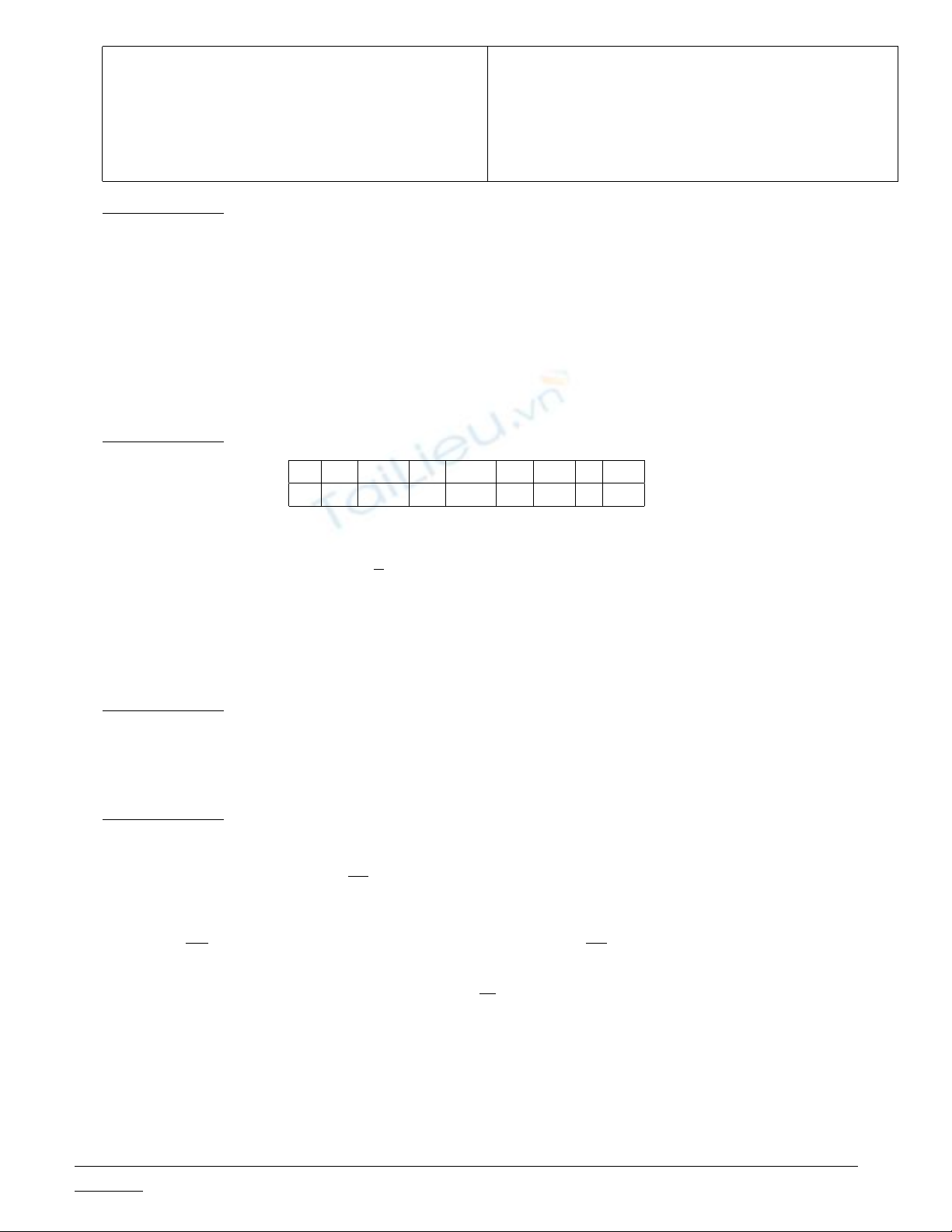
Câu 2. (2.5đ) Cho số liệu:
X 0 0.5 1 1.5 2 2.5 3 3.5
Y 31 29.3 26 22.1 16 13 7 1.7
Áp dụng phương pháp Bình phương bé nhất theo các yêu cầu:
a. Với dạng đường cong Y=A+B√x, thì A= (6) và B= (7). Sử dụng kết quả này, để Y= 0 thì
X= (8).
b. Hãy chọn một giá trị x0= (9) để có thể tìm được dạng đường cong Y=A+Bln(X+x0). Khi
đó thì A= (10).
Câu 3. (2.5đ) Xét phương trình: f(x)=2x2+ 4x−ex= 0 trên khoảng tách nghiệm x∈[3; 5].
Áp dụng phương pháp Newton, hãy cho biết x0= (11), x1= (12), x3= (13). Tìm min
3≤x≤5|f0(x)|=
(14) và sai số |x−x3| ≤ (15).
Câu 4. (2.5đ) Phương pháp Simpson 3:8 có công thức: (a≤b)
b
Z
a
f(x)dx ≈3h
8[f(a)+3f(a+h)+3f(a+ 2h) + f(b)] ,
trong đó h=b−a
3. Công thức này có sai số tuyệt đối không quá 3h5
80 max
a≤x≤b|f(4)(x)|.
a. Áp dụng công thức trên tính gần đúng I=
0.3
R
0
√exdx ≈(16), khi đó sai số tuyệt đối là (17). Nếu
tính Ibằng công thức Simpson 4 đoạn chia thì sai số tuyệt đối không quá (18).
b. Trong ý (19), hãy nêu một sự khác biệt giữa công thức Simpson 3:8 và công thức Simpson.
Trong ý (20), hãy nêu một ưu điểm về sai số của công thức Simpson 3:8 so với công thức
Simpson.
Ghi chú: -Cán bộ coi thi không giải thích đề thi.
1
Họ và tên . . . Giám thị 1 . . . . . . Giám thị 2 . . . . . .
MSSV . . . Điểm . . . . . . Điểm chữ . . . . . .
STT . . . Giáo viên chấm . . .
Ý Đáp án Ý Đáp án
(1) 0.140 (10) A=35.916
(2) 0.2246 (11) x0= 5 (có thể khác)
(3) 0.2039 (12) x1= 4.369...
(4) 0.1403 (13) x3= 3.7998...
(5) 0.2036 (14) e3−16
(6) 37.059 (15) ∆≤5.10−1
(7) -15.779 (16) 0.3236
(8) 5.5160 (17) 3.10−8
(9) x0= 1 (có thể khác) (18) 2.10−8
(19) Simpson: n chẵn (20) Độ hội tụ của sai số
Simpson 3:8 : n chia hết 3 của ct simpson thấp hơn (bậc 4 so với 5)
2
TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT ĐỀ THI CUỐI KỲ HỌC KỲ I NĂM HỌC 18-19
THÀNH PHỐ HỒ CHÍ MINH Môn: PHƯƠNG PHÁP TÍNH
KHOA KHOA HỌC ỨNG DỤNG Mã môn học: MATH121101
BỘ MÔN TOÁN Đề thi số 101110 - Đề thi có 2 trang.
***** Thời gian 75 phút. Được phép sử dụng tài liệu
Câu 1. (2.5đ) Cho bài toán Cauchy:
(y0(x) = xy2+ 0.2
y(0) = 0.3
a. Áp dụng phương pháp Euler, h=0.1, tính gần đúng y(0.2) ≈(1), y(0.6) ≈(2). Từ đó suy ra
y0(0.2) ≈(3).
b. Áp dụng phương pháp Euler cải tiến, h=0.1, tính gần đúng y(0.2) ≈(4), y(0.5) ≈(5).
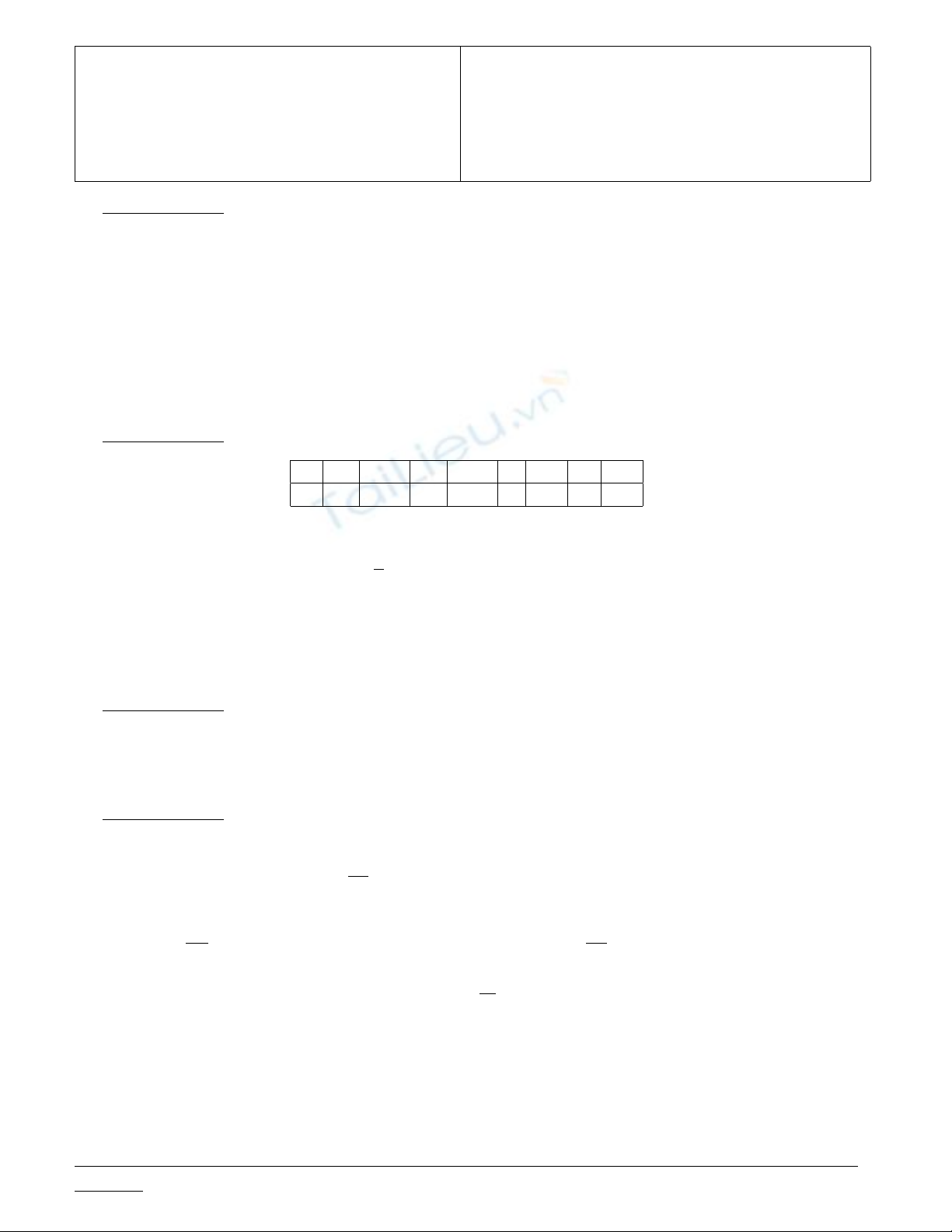
Câu 2. (2.5đ) Cho số liệu:
X 0 0.5 1 1.5 2 2.5 3 3.5
Y 21 19.3 16 12.1 6 3 -3 -8
Áp dụng phương pháp Bình phương bé nhất theo các yêu cầu:
a. Với dạng đường cong Y=A+B√x, thì A= (6) và B= (7). Sử dụng kết quả này, để Y= 0 thì
X= (8).
b. Hãy chọn một giá trị x0= (9) để có thể tìm được dạng đường cong Y=A+Bln(X+x0). Khi
đó thì A= (10).
Câu 3. (2.5đ) Xét phương trình: f(x)=2x2+ 5x−ex= 0 trên khoảng tách nghiệm x∈[3; 5].
Áp dụng phương pháp Newton, hãy cho biết x0= (11), x1= (12), x3= (13). Tìm min
3≤x≤5|f0(x)|=
(14) và sai số |x−x3| ≤ (15).
Câu 4. (2.5đ) Phương pháp Simpson 3:8 có công thức: (a≤b)
b
Z
a
f(x)dx ≈3h
8[f(a)+3f(a+h)+3f(a+ 2h) + f(b)] ,
trong đó h=b−a
3. Công thức này có sai số tuyệt đối không quá 3h5
80 max
a≤x≤b|f(4)(x)|.
a. Áp dụng công thức trên tính gần đúng I=
0.3
R
0
3
√exdx ≈(16), khi đó sai số tuyệt đối là (17). Nếu
tính Ibằng công thức Simpson 4 đoạn chia thì sai số tuyệt đối không quá (18).
b. Trong ý (19), hãy nêu một sự khác biệt giữa công thức Simpson 3:8 và công thức Simpson.
Trong ý (20), hãy nêu một ưu điểm về sai số của công thức Simpson 3:8 so với công thức
Simpson.
Ghi chú: -Cán bộ coi thi không giải thích đề thi.
3
Họ và tên . . . Giám thị 1 . . . . . . Giám thị 2 . . . . . .
MSSV . . . Điểm . . . . . . Điểm chữ . . . . . .
STT . . . Giáo viên chấm . . .
Ý Đáp án Ý Đáp án
(1) 0.341 (10) A=25.866
(2) 0.4418 (11) x0= 5 (có thể khác)
(3) 0.223 (12) x1= 4.405...
(4) 0.342 (13) x3= 3.930...
(5) 0.4177 (14) e3−17
(6) 27.00 (15) ∆≤4.10−1
(7) -15.70 (16) 0.3155
(8) 2.9578 (17) .610−9
(9) x0= 1 (có thể khác) (18) 3.10−9
(19) Simpson: n chẵn (20) Độ hội tụ của sai số
Simpson 3:8 : n chia hết 3 của ct simpson thấp hơn (bậc 4 so với 5)
Chuẩn đầu ra của học phần (Về kiến thức) Nội dung K.Tra
[G1.7]: Có khả năng vận dụng các phương pháp Euler, Euler cải tiến vào giải
các phương trình vi phân thường với điều kiện điểm đầu. Câu 1
[G1.5]: Có khả năng áp dụng công thức công thức Simpson vào tính gần đúng
và đánh giá sai số các tích phân xác định cụ thể. Câu 4
[G1.6]: Nắm bắt ý nghĩa phương pháp bình phương bé nhất và vận dụng tìm
một số đường cong cụ thể từ phương pháp này Câu 2
[G2.3]: Có khả năng áp dụng các phương pháp lặp, phương pháp Newton vào
giải gần đúng và đánh giá sai số các phương trình đại số cụ thể Câu 3
TP.HCM, ngày 15 tháng 12 năm 2018
Thông qua bộ môn
Nguyễn Văn Toản
4