

1>] C^@C C>B_ C^@C C>`
'1*?4!$<
:#-
: 
:$
1>] C^@C C>B_ C^@C C>`
'1*?4!$<
Với những phép toán này, ta không
chỉ tạo ra các đối tượng mà còn hỗ
trợ các thao tác phức tạp hơn.
Ví dụ, ta có thể thêm vào
hoặc loại bỏ bớt các đối
tượng đã vẽ
1>] C^@C C>B_ C^@C C>`
'1*?4!$< 1>] C^@C C>B_ C^@C C>`
'1*?4!$<
Boundary Representation (B:rep)
Khi hình h;c biên
• Mct mô hình Brep là mô hình đưYc bao
bwi các mEt biên. Các mEt này:
– Kín và liên tHc
– Có th` đbnh hư4ng, nghĩa là có th` phân
bi.t hai phía.
1>] C^@C C>B_ C^@C C>`
Các phn m6m CAD/CAM thương m#i thưng có th` bi`u
disn vUt th` 3D w 2 d#ng:
Gần đúng
Chính xác
Boundary Representation (B:rep)
1>] C^@C C>B_ C^@C C>`


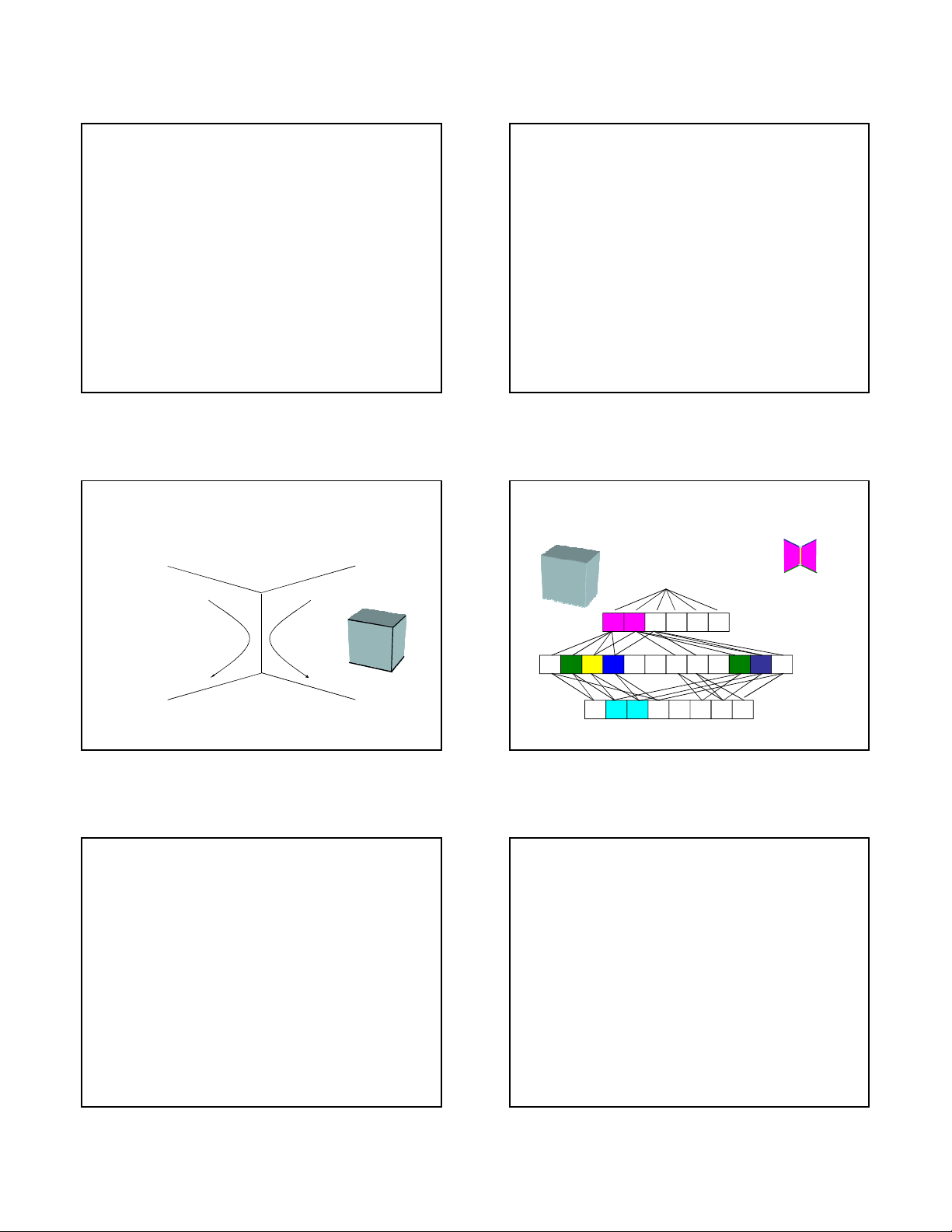
Boundary Representation (B:rep)
• Các phn to hình h&c
– Đi`m = points
– Đưng = curves
– MEt = surfaces
• Chúng đưYc t#o ra, hi.u ch^nh và xo lý
theo phép toán cRa hình h&c Euclid
1>] C^@C C>B_ C^@C C>`
• C'u trúc d, li.u cRa mct c#nh :
– Mct c#nh
• ĐưYc bao bwi hai đ^nh
• Tip giáp chính xác v4i hai mEt
• Mhi mct c#nh tham gia hai vòng lEp,.
• Các vòng lEp đưYc đbnh hư4ng
– Trư4c
– Sau
Boundary Representation (B:rep)
1>] C^@C C>B_ C^@C C>`
!
"


#"
#!
"
!
 
"
"
#"
#!
"
!
Boundary Representation (B:rep)
1>] C^@C C>B_ C^@C C>`
!"
$
!
"
$
%
&
'
(
!
"
$
%
'
(
!)
!!
!"

&
*
%
$
"
!
&
*
%
$
"
!!"
!!
!)
+
(
'
%
$
"
! (
'
&
*
, 
- 
.
 
/
Boundary Representation (B:rep)
1>] C^@C C>B_ C^@C C>`
• Các phn to Topologic là
– đ^nh = vertices
– c#nh = edges
– mEt = faces
– Vòng lEp = loops
Boundary Representation (B:rep)
1>] C^@C C>B_ C^@C C>`
• Các phn to Topologic đưYc t#o ra và
ch^nh lý bwi các toán to Euler
• Các toán to Euler
– đPm bPo tính thOng nh't cRa model
– cho mct cơ ch ki`m tra si chuc chun cRa
model
Boundary Representation (B:rep)
1>] C^@C C>B_ C^@C C>`


•Các toán t> Euler:
1>] C^@C C>B_ C^@C C>`
Thí dB: xây dDng mFt khi tG din dùng
toán t> Euler
1>] C^@C C>B_ C^@C C>`
Thí dB: xây dDng mFt khi tG din dùng
toán t> Euler (tip theo)
1>] C^@C C>B_ C^@C C>`
• Công thc EulerPoincaré:
VE+F(LF) 2(SG) = 0
• V  sO lưYng vertices (đ^nh)
• F  sO lưYng faces (mEt)
• E  sO lưYng edges (c#nh)
• L  sO lưYng loops (vòng biên kín ngoài hay trong
các mEt)
• S  sO lưYng shell (vg. bPn thân mct khOi solid đã
là mct vg, nên giá trb nhg nh't cRa vg bang 1)
• G  sO lưYng genus (lh xuyên qua khOi)
Boundary Representation (B:rep)
1>] C^@C C>B_ C^@C C>`
Thí dụ
Boundary Representation (B:rep)
1>] C^@C C>B_ C^@C C>`
B:rep và CSG
• CSG
– Các phn to cơ cw là nguyên thu}
– Phép toán: dùng các toán to boolean
– C'u trúc d, li.u
• Cây nhb phân
• G&n nhŽ
1>] C^@C C>B_ C^@C C>`

*
• Brep
– Các phn to cơ bPn: đ^nh, mEt, c#nh
(vertices, faces, edges)
– Toán to: toán to Euler
– C'u trúc d, li.u:
• C'u trúc c#nh ki`u cánh (Wing edge structure)
• Không gian bc nh4 l4n
aE% #2:(:#&:$ ::7Y :,:6:
2 :%0:% :+:4::% :(:"K:%:đó
đưYc dùng nhi6u trong các h. thOng CADCAM
B:rep và CSG
1>] C^@C C>B_ C^@C C>`
• Kr thuUt Voxel
• Kr thuUt Grammar (nhân mPnh)
• Kr thuUt Particle (t#o h#t)
D"AE?F>D"D
1>] C^@C C>B_ C^@C C>`
•TJo bKi mFt tLp khi
lLp phương nh
– Không gian ba chi6u
đưYc chia ra thành
nh,ng khOi (t bào)
lUp phương nhg v4i
đc phân giPi cho
trư4c và khOi vUt th`
đưYc mô hình hoá
bang cách li.t kê
danh sách các t bào
mà nó chim gi,.
KỸ THUẬT VOXEL
1>] C^@C C>B_ C^@C C>`
Ưu nhưc đim ca Voxel
Ưu điểm:
• Đơn giản
• Độ phức tạp như nhau cho tất cả các đối tượng
• Dùng các tóan tử Boolean
hược điểm:
• Chỉ gần đúng
• Đòi hỏi bộ nhớ lớn
• Màn hình đắt tiền
Dùng chủ yếu trong các máy Scanner trong y học
1>] C^@C C>B_ C^@C C>`
5)9@,,' !(:#>"
(%"d)_:8"
@
"'@!AA:)W=
W"(e88*8:'@W=
2*!"!8(::)#>
;)98((87
nhân mnh)
1>] C^@C C>B_ C^@C C>` articles (To ht)
A#Ae"(:="
'@!'(:)W;"W<'WAW=^=X
"% '@#<'9!"
!;"' W<<%7W
!'@"
"!%"8A)bA(@
WWd)9!W="bA(
;"
Cb*"!#$'@#@<'!
b#'8!<'!W<'!'8'@W=^=X
1>] C^@C C>B_ C^@C C>`

/
Ọ
"<'9 ( (
=@"8'@<'!%eb
&:A)^5!b%W
"8==!
(!
!(='"!K
2!"(:%:'
2!(:)
1>] C^@C C>B_ C^@C C>`
TÓM LƯOC
• Có nhi6u cách t#o mô hình
– 2D
– 3D
• Khung dây
• MEt
• KhOi ( Crep, Brep, Voxel, Grammar,
Particles, Drop)
• Hi`u bit và so dHng chúng trong công tác
thit k sPn ph2m sq r't thuUn lYi.
1>] C^@C C>B_ C^@C C>`
G$EHGI%J8K,%JLMN2%O$8P,%,>Q8%,8/%D8R%
CES%+T,$%$US"%,8/V,82
a , -  BD & # 6 2
" - 4 J!+ %$ (   6
@$ 6 2 + ,I
E  $ -   # # "K #V
! ( 
E  G 2  #$ ! (  ;6.#
$#  64& #$=
E   6.# $# $ - 
1>] C^@C C>B_ C^@C C>`
E Y  # $ K# 4" ! ,  $&
.#3  & "    6  
( 
E Y 1- -  .#  BDB1 # ,
.#  ,  & )  $ - BD
 B1 ! 
E Y F-#  #&  BD  B1 , "&#
!& K# (- #& -  BDB1
1>] C^@C C>B_ C^@C C>`
1>] C^@C C>B_ C^@C C>`
'1*?4!$< '1*?4!$<
1>] C^@C C>B_ C^@C C>`