MÔ HÌNH T H I QUY VECTOR VAR - MÔ HÌNH VETOR HI U CH NHỰ Ồ Ệ Ỉ
SAI S VECMỐ
I- T H I QUY VECTO (VAR)Ự Ồ
Nh chúng ta bi t, m i quan h gi a các bi n s kinh t không đ n thu n chư ế ố ệ ữ ế ố ế ơ ầ ỉ
theo m t chi u, bi n đ c l p (bi n gi i thích) nh h ng lên bi n ph thu c màộ ề ế ộ ậ ế ả ả ưở ế ụ ộ
trong nhi u tr ng h p nó còn có nh h ng ng c l i. Do đó mà ta ph i xétề ườ ợ ả ưở ượ ạ ả
nh h ng qua l i gi a các bi n này cùng m t lúc. Chính vì th mô hình kinh tả ưở ạ ữ ế ộ ế ế
l ng mà ta ph i xét đ n không ph i là mô hình m t ph ng trình mà là mô hìnhượ ả ế ả ộ ươ
nhi u ph ng trình.ề ươ
Tuy nhiên, đ c l ng đ c các mô hình này ta ph i đ m b o r ng cácể ướ ượ ượ ả ả ả ằ
ph ng trình trong h đ c đ nh d ng, m t s bi n đ c coi là n i sinh (bi nươ ệ ượ ị ạ ộ ố ế ượ ộ ế
mà giá tr đ c xác đ nh b i mô hình, là bi n ng u nhiên) và m t s bi n khácị ượ ị ở ế ẫ ộ ố ế
đ c coi là ngo i sinh hay đã xác đ nh tr c (ngo i sinh c ng v i n i sinh tr ).ượ ạ ị ướ ạ ộ ớ ộ ễ
Vi c đ nh d ng này th ng đ c th c hi n b ng cách gi thi t r ng m t sệ ị ạ ườ ượ ự ệ ằ ả ế ằ ộ ố
bi n đ c xác đ nh tr c ch có m t trong m t s ph ng trình. Quy t đ nh nàyế ượ ị ướ ỉ ặ ộ ố ươ ế ị
th ng mang tính ch quan và đã b Chrishtopher Sims ch trích. Theo Sims, n uườ ủ ị ỉ ế
t n t i m i quan h đ ng th i gi a m t s bi n thì các bi n này ph i đ c xétồ ạ ố ệ ồ ờ ữ ộ ố ế ế ả ượ
có vai trò nh nhau, t c là t t c các bi n xét đ n đ u là bi n n i sinh. D a trênư ứ ấ ả ế ế ề ế ộ ự
tinh th n đó mà Sims đã xây d ng mô hình vector t h i quy Var.ầ ự ự ồ
1. Khái ni mệ
Mô hình Var v c u trúc g m nhi u ph ng trình (mô hình h ph ng trình) vàề ấ ồ ề ươ ệ ươ
có các tr c a các bi n s . Var là mô hình đ ng c a m t s bi n th i gian.ễ ủ ế ố ộ ủ ộ ố ế ờ
Ta xét hai chu i th i gian Yỗ ờ 1 và Y2. Mô hình Var t ng quát đ i v i Yổ ố ớ 1 và Y2 có
d ng sau đây:ạ
Trong mô hình trên, m i ph ng trình đ u ch a p tr c a m i bi n. V i hai bi nỗ ươ ề ứ ễ ủ ỗ ế ớ ế
mô hình có 22p h s góc và 2 h s ch n. V y trong tr ng h p t ng quát n uệ ố ệ ố ặ ậ ườ ợ ổ ế
mô hình có k bi n thì s có kế ẽ 2p h s góc và k h s ch n, khi k càng l n thì sệ ố ệ ố ặ ớ ố
h s ph i c l ng càng tăng.ệ ố ả ướ ượ
2. M t s v n đ trong xây d ng mô hình Var:ộ ố ấ ề ự
Bên c nh nh ng u đi m n i tr i c a mô hình Var : không c n xác đ nh bi n nàoạ ữ ư ể ổ ộ ủ ầ ị ế
là bi n n i sinh và bi n nào là bi n ngo i sinh hay là ta có th s d ng ph ngế ộ ế ế ạ ể ử ụ ươ
pháp OLS cho t ng ph ng trình riêng r thì mô hình Var còn v ng ph i m t sừ ươ ẽ ướ ả ộ ố
h n ch : ạ ế
- Do tr ng tâm mô hình đ c đ t vào d báo nên Var ít phù h p cho phân tíchọ ượ ặ ự ợ
chính sách.
-Và khi xét đ n mô hình Var ta còn ph i xét đ n tính d ng c a các bi n trongế ả ế ừ ủ ế
mô hình. Yêu c u đ t ra khi ta c l ng mô hình Var là t t c các bi n ph iầ ặ ướ ượ ấ ả ế ả
d ng, n u trong tr ng h p các bi n này ch a d ng thì ta ph i l y sai phânừ ế ườ ợ ế ư ừ ả ấ
đ đ m b o chu i d ng. Càng khó khăn h n n a n u m t h n h p ch a cácể ả ả ỗ ừ ơ ữ ế ộ ỗ ợ ứ
bi n có tính d ng và các bi n không có tính d ng thì vi c bi n đ i d li uế ừ ế ừ ệ ế ổ ữ ệ
không ph i là vi c d dàng.ả ệ ễ
-Khó khăn trong vi c l a ch n kho ng tr thích h p. Gi s mô hình Var b nệ ự ọ ả ễ ợ ả ử ạ
đang xét có ba bi n và m i bi n s có 8 tr đ a vào t ng ph ng trình. Nhế ỗ ế ẽ ễ ư ừ ươ ư
xem xét trên thì s h s mà b n ph i c l ng là 3ở ố ệ ố ạ ả ướ ượ 2.8+3=75. Và n u taế
tăng s bi n và s tr đ a vào m i ph ng trình thì s h s mà ta ph i cố ế ố ễ ư ỗ ươ ố ệ ố ả ướ
l ng s khá l n. Ngoài ra, khó khăn trong vi c l a ch n kho ng tr cònượ ẽ ớ ệ ự ọ ả ễ
đ c th hi n ch n u ta tăng đ dài c a tr s làm cho b c t do gi m,ượ ể ệ ở ỗ ế ộ ủ ễ ẽ ậ ự ả
do v y mà nh h ng đ n ch t l ng các c l ng.ậ ả ưở ế ấ ượ ướ ượ
3. Ph ng pháp c l ng mô hình Var:ươ ướ ượ
- Xét tính d ng c a các bi n trong mô hình. N u ch a d ng thì s d ng kừ ủ ế ế ư ừ ử ụ ỹ
thu t l y sai phân đ đ a v các chu i d ng.ậ ấ ể ư ề ỗ ừ
-L a ch n kho ng tr phù h p.ự ọ ả ễ ợ
- Xem xét m c đ phù h p c a mô hình ch y ra (b ng vi c ki m đ nh tínhứ ộ ợ ủ ạ ằ ệ ể ị
d ng c a ph n d . N u ph n d c a mô hình d ng thì mô hình nh n đ cừ ủ ầ ư ế ầ ư ủ ừ ậ ượ
phù h p v i chu i th i gian và ng c l iợ ớ ỗ ờ ượ ạ
-So sánh các mô hình phù h p và l a ch n mô hình phù h p nh t.ợ ự ọ ợ ấ
Ví d ta ch y mô hình Var cho chu i s li u v tiêu dùng (CS) và thu nh p sauụ ạ ỗ ố ệ ề ậ
thu (Y) trong th i kỳ quý I/1974 – IV/1984 c a Anh. ( File d li u đính kèm)ế ờ ủ ữ ệ
Tr c tiên ta ki m đ nh tính d ng đ i v i 2 chu i d li u CS và Y ta th y:ướ ể ị ừ ố ớ ỗ ữ ệ ấ
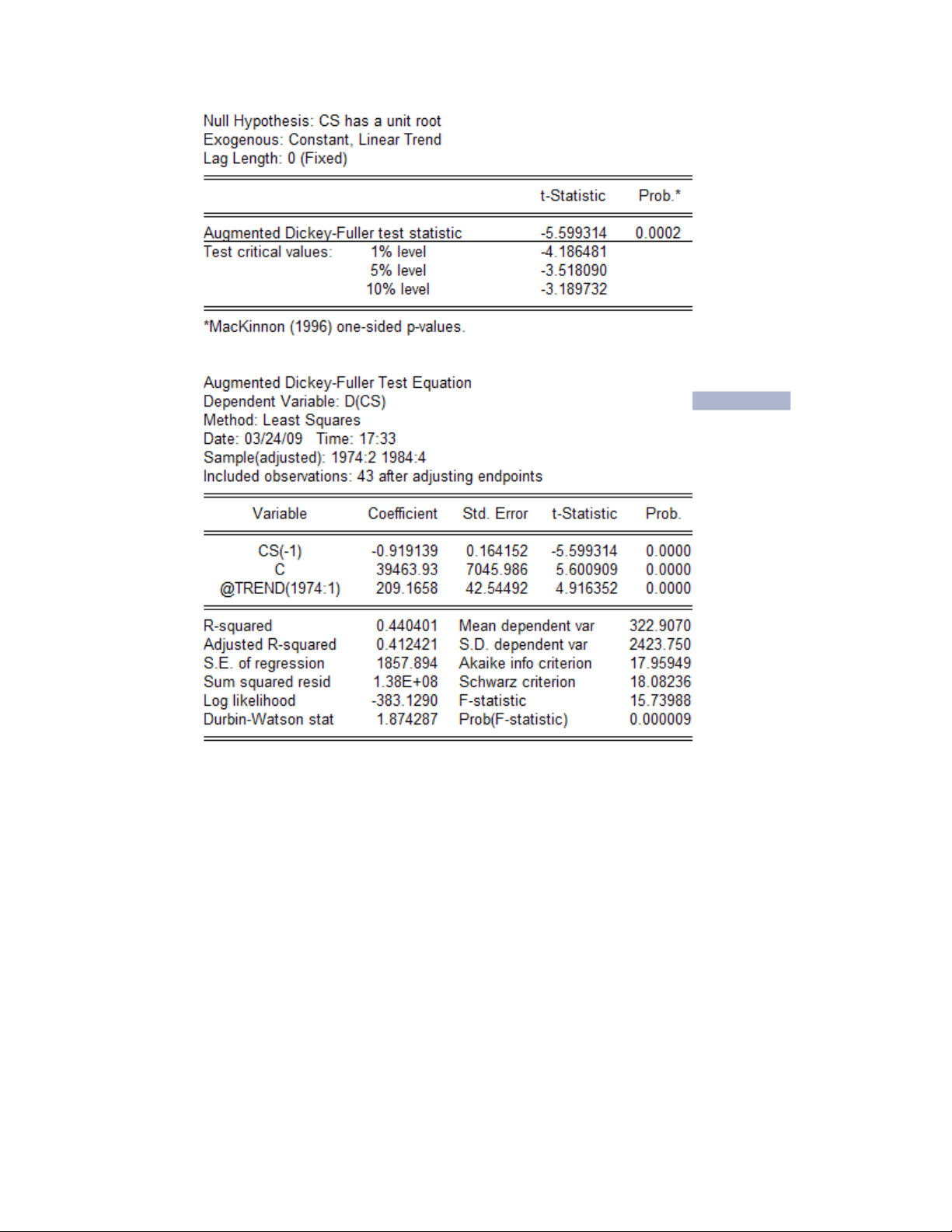
Theo ki m đ nh Dickey-Fuller thì chu i CS là chu i d ng (giá tr |t| = 5,599 l nể ị ỗ ỗ ừ ị ớ
h n các giá tr th ng kê t ng ng c 3 m c ý nghĩa 1%, 3% và 5%)ơ ị ố ươ ứ ở ả ứ
Ch y t ng t ng t đ i v i chu i yạ ươ ươ ự ố ớ ỗ
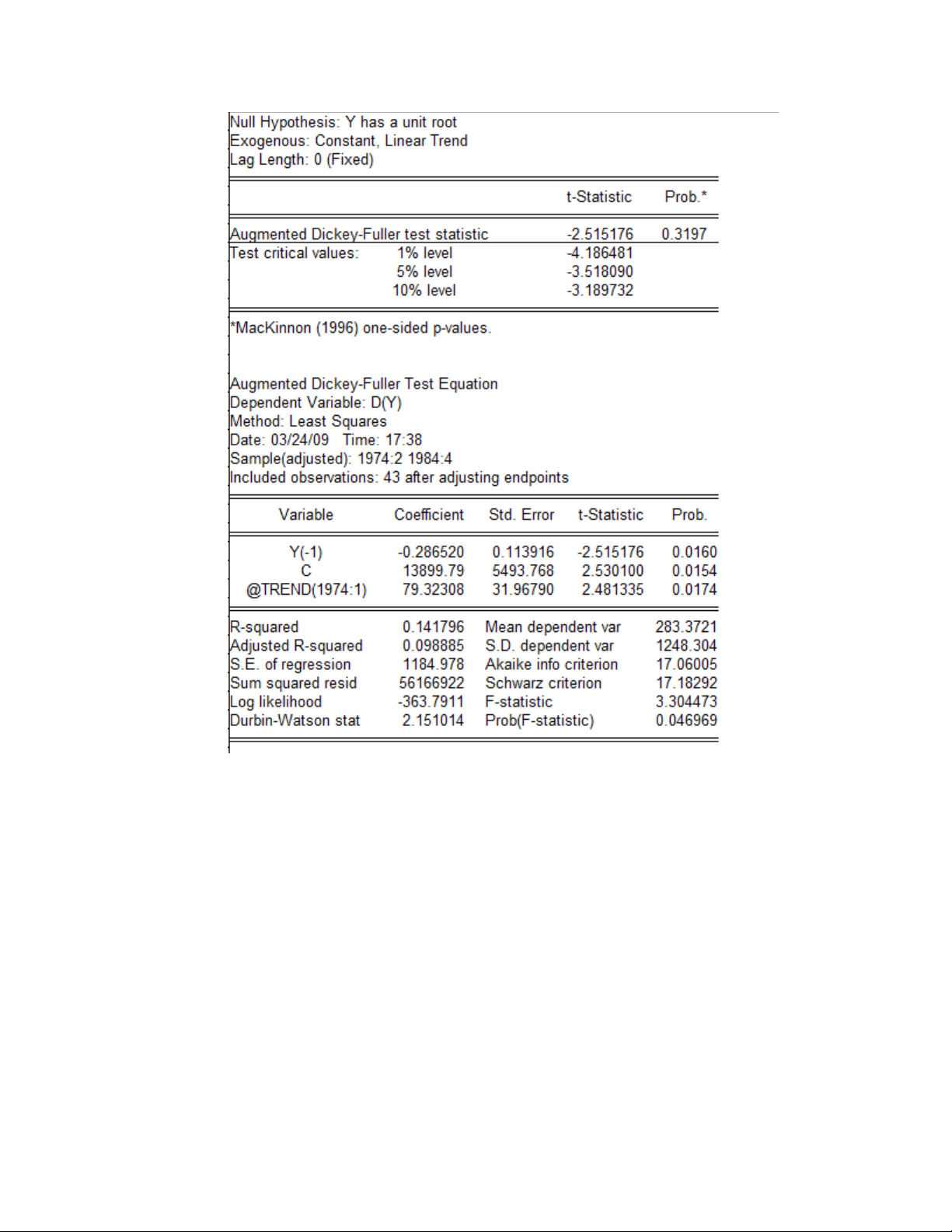
Chu i y là chu i không d ng. Và khi l y sai phân cho chu i này thì ta nh n đ cỗ ỗ ừ ấ ỗ ậ ượ
m t chu i d ng.ộ ỗ ừ