TRƯỜNG ĐH SƯ PHẠM TP HỒ CHÍ MINH
KHOA TOÁN – TIN HỌC
Tài liệu hỗ trợ môn HÌNH VI PHÂN
Trích bài giảng và bài tập của thầy Nguyễn Hà Thanh
sinh viên thực hiện Nguyễn Thành An
Học phần
MẶT TRONG KHÔNG GIAN
3
¡
Tp. Hồ chí minh – 8/2008
2
MỘT SỐ KIẾN THỨC CƠ BẢN
1. Mặt tham số.
Cho
U
là tập mở trong
2
¡
, hàm véctơ
( ) ( )
3
:
, ,
r U
®
¡
a
là mặt tham số nếu
r
là ánh xạ khả vi
trên
U
. Khi đó
(
)
r U
là giá của mặt tham số.
Hai mặt tham số ~
~
3 3
: , :r U r U® ®
¡ ¡
là tương đương nếu tồn tại vi phôi
~
:
U U
j
® sao cho
~0
r r
j
=, ký hiệu
~
r r
:
. Nếu hai mặt tham số tương đương với nhau thì giá của chúng trùng nhau.
2. Mặt đơn.
Cho mặt
(
)
S
có tham số hóa
r
, nếu
r
đơn ánh thì
(
)
S
là mặt đơn.
3. Mặt chính qui.
Cho mặt
(
)
S
có tham số hóa
( ) ( )
3
:
, ,
r U
u v r u v
®
¡
a
. Khi đó
(
)
0 0
,
M r u v
= là điểm chính qui của
mặt
(
)
S
nếu hai véctơ
(
)
(
)
0 0 0 0
' , , ' ,
u v
r u v r u v
độc lập tuyến tính. Nếu mặt
(
)
S
chính qui tại mọi
điểm
(
)
,
M r u v
=, với
(
)
,
u v U
Î
thì
(
)
S
là mặt chính qui. Điểm không chính qui là điểm kỳ dị.
Tính chính qui của mặt
(
)
S
không phụ thuộc vào biểu diễn tham số (các bạn tự chứng minh).
Nếu tại điểm
(
)
0 0
,
M r u v
= là điểm chính qui của mặt
(
)
S
thì phương trình mặt phẳng tiếp
xúc hay tiếp diện tại điểm
(
)
0 0 0
, ,
M x y z
nhận
(
)
(
)
0 0 0 0
' , , ' ,
u v
r u v r u v
làm cặp véctơ chỉ phương có
dạng
( ) ( ) ( )
( ) ( ) ( )
0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
' , ' , ' , 0
' , ' , ' ,
u u u
v v v
x x y y z z
x u v y u v z u v
x u v y u v z u v
- - -
=
.
Đường thẳng vuông góc với mặt phẳng tiếp xúc tại điểm
(
)
0 0
,
M r u v
= là pháp tuyến có
phương trình
0 0 0
x x y y z z
a b c
- - -
= = với
, ,
a b c
được tính bởi
(
)
(
)
( ) ( )
0 0 0 0
0 0 0 0
' , ' ,
' , ' ,
u u
v v
y u v z u v
a
y u v z u v
=,
(
)
(
)
( ) ( )
0 0 0 0
0 0 0 0
' , ' ,
' , ' ,
u u
v v
z u v x u v
b
z u v x u v
=,
(
)
(
)
( ) ( )
0 0 0 0
0 0 0 0
' , ' ,
' , ' ,
u u
v v
x u v y u v
c
x u v y u v
=, hơn nữa không gian sinh bởi
(
)
(
)
0 0 0 0
' , , ' ,
u v
r u v r u v
tại điểm
(
)
0 0
,
M r u v
= là không gian tiếp xúc với mặt
(
)
S
tại điểm
M
,
ký hiệu
(
)
M
T S
. Khi đó
(
)
(
)
( )
M
M S
T S T S
Î
=
U
là tập tất cả các không gian tiếp xúc.
4. Đường trên mặt.
Phaàn 1
3
Cho mặt
(
)
S
chính qui có tham số hóa
( ) ( )
3
:
, ,
r U
u v r u v
®
¡
a
và
(
)
x
là đường trong
U
có tham số
(
)
( )
u u t
v v t
ì =
ï
í=
ï
î
,
t I
Î
qua
r
cho ta đường cong
(
)
(
)
S
x
Ì
có
( ) ( ) ( )
( )
3
:
,
I
t t r u t v t
j
j
®
=
¡
a
.
Ta khảo sát 2 trường hợp đặc biệt sau.
Trường hợp 1.
0
v v
=
tương ứng với đường
(
)
( )
0
r
u u t
v v
x
ì =
ï¾¾®
í=
ï
î có
(
)
(
)
(
)
0
,
t u t v
j
=. Ta nói
đây là họ tham số thứ nhất trên mặt
(
)
S
. Các tiếp tuyến của đường tham số thứ nhất có phương là
(
)
' ,
u
r u v
.
Trường hợp 2.
0
u u
=
tương ứng với đường
( ) ( )
0r
u u
v v t
x
=
ì
ï¾¾®
í=
ï
î có
(
)
(
)
(
)
0,
t u v t
j
=. Ta nói
đây là họ tham số thứ hai trên mặt
(
)
S
. Các tiếp tuyến của đường tham số thứ hai có phương là
(
)
' ,
v
r u v
.
5. Mặt định hướng, véctơ pháp tuyến đơn vị trên mặt định hướng.
Cho mặt
(
)
S
chính qui có tham số hóa
( ) ( )
3
:
, ,
r U
®
¡
a
, theo trên hai mặt tham số hóa gọi là
tương đương nếu tồn tại vi phôi
~
:
U U
j
® sao cho ~0
r r
j
=. Như ta đã biết
~ ~
~ ~
~
~
~ ~
' ' ' '
u v
u v
J
d u d v
du dv
r r r r
d u d v
dv du
Ù = Ù
14243
, nếu
0
J
>
thì
(
)
S
là mặt định hướng được.
Cho mặt
(
)
S
định hướng ta luôn có
~ ~
~ ~
' ' ' '
' '
' '
u v u v
u v
u v
r r r r
r r
r r
Ù Ù
=
ÙÙ
. Tại mọi điểm
(
)
,
M r u v
= ta luôn có
một véctơ đơn vị
( )
' '
,
' '
u v
u v
r r
n u v
r r
Ù
=Ù là véctơ pháp tuyến đơn vị của
(
)
S
.
6. Dạng toàn phương cơ bản thứ nhất.
Cho mặt
(
)
S
chính qui có tham số hóa
( ) ( )
3
:
, ,
r U
®
¡
a
. Xét dạng toàn phương
(
)
( )
:
,
M
I T S
a I a a a
®
=
¡
a
. Khi đó công thức dạng toàn phương cơ bản thứ nhất có dạng
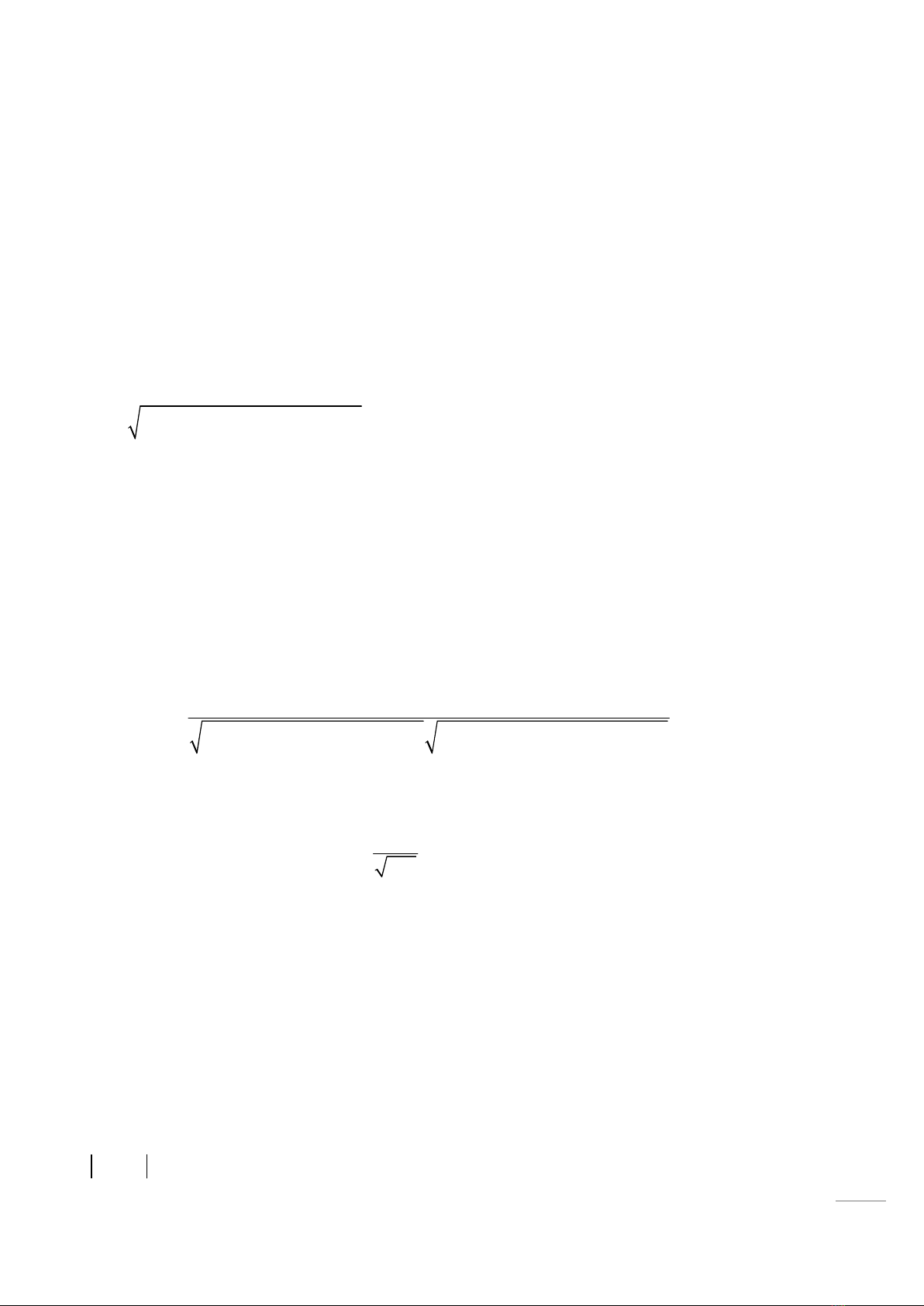
4
(
)
(
)
(
)
2 2
2
u u v v
I a E a Fa a G a
= + + với
, ,
E F G
được xác định bởi
( )
(
)
2
' ,
u
E r u v
=,
(
)
(
)
' , . ' ,
u v
F r u v r u v
=
,
( )
(
)
2
' ,
v
G r u v
=.
Đối với dạng toàn phương cơ bản thứ nhất ta thường quen nhìn ở dạng
(
)
(
)
(
)
2 2
2
I a E du Fdudv G dv
= + + .
7. Công thức tính độ dài cung trên mặt.
Cho mặt
(
)
S
chính qui có tham số hóa
( ) ( )
3
:
, ,
r U
®
¡
a
và đường cong
(
)
x
có tham số
(
)
(
)
(
)
(
)
[
]
, , ,
t r u t v t t a b
j
= Î . Khi đó công thức tính độ dài cung trên mặt là
( ) ( )
2 2
' 2 ' ' '
b
t t t t
a
l E u Fu v G v dt
= + +
ò, với
, ,
E F G
được xác định như trên.
8. Công thức góc giữa hai đường cong trên mặt.
Cho mặt
(
)
S
chính qui có tham số hóa
( ) ( )
3
:
, ,
r U
u v r u v
®
¡
a
và hai đường cong
(
)
1
x
có
(
)
(
)
(
)
(
)
(
)
1 1
1 1 1 1 1 1
, , ' ' ' ' '
u v
t r u t v t t r u r v
j j
= = +
(
)
2
x
có
(
)
(
)
(
)
(
)
(
)
2 2
2 2 2 2 2 2
, , ' ' ' ' '
u v
t r u t v t t r u r v
j j
= = +
(
1 2 1 2
, , ,
u u v v
đều lấy đạo hàm theo biến
t
).
Khi đó công thức tính góc giữa 2 đường cong
(
)
1
x
và
(
)
2
x
là
·
( )
(
)
( ) ( ) ( ) ( )
1 2 1 2 2 1 1 2
1, 2
2 2 2 2
1 1 1 1 2 2 2 2
' ' ' ' ' ' ' '
os
' 2 ' ' ' ' 2 ' ' '
Eu u F u v u v Gv v
c
E u Fu v G v E u Fu v G v
x x
+ + +
=+ + + + .
Trong trường hợp đặc biệt.
Nếu
(
)
1
x
có
(
)
(
)
(
)
1 0
,
t r u t v
j
=,
(
)
2
x
có
(
)
(
)
(
)
2 0 ,
t r u v t
j
= thì
(
)
1
' ' '
u t
t r u
j
=,
(
)
2
' ' '
v t
t r v
j
=. Khi đó
·
(
)
1, 2
os
F
c
EG
x x
=.
9. Ánh xạ Weingarten.
Xét ánh xạ
(
)
(
)
:M M
h T S T S
®
thỏa mãn
(
)
( )
' ' '
' ' '
h
u u u
h
v v v
r h r n
r h r n
ì
¾¾® = -
ï
í¾¾® = -
ï
î
và
( )
(
)
(
)
: ' ' ' ' ' '
h
u u v v u u v v u u v v
M S
a T a a r a r a a n a n a n a n
Î = + ¾¾® = - + - = - - .
ta gọi ánh xạ
h
được xác định như trên là ánh xạ Weingarten (ánh xạ định dạng của
(
)
S
). Khi đó
[
]
det
h
là độ cong Gauss của
(
)
S
và các giá trị riêng của ma trận
[
]
h
gọi là độ cong chính.
Nhận xét.
h
là ánh xạ tuyến tính, cách xác định ánh xạ tuyến tính
h
không phụ thuộc vào
tham số. Ma trận của ánh xạ tuyến tính
h
là ma trận cấp 2,
l
là giá trị riêng của ma trận
h
nếu
0
A I
l
- =
. Ánh xạ Weingarten là ánh xạ tuyến tính đối xứng, tự liên hợp.
5
10. Dạng toàn phương cơ bản thứ hai.
Cho mặt
(
)
S
chính qui có tham số hóa
( ) ( )
3
:
, ,
r U
u v r u v
®
¡
a
Ánh xạ
(
)
(
)
( ) ( ) ( ) ( )
:
, , . .
M M
II T S T S
a b I a b h a b a h b
®
= =
a
là dạng song tuyến tính đối xứng. Khi đó
(
)
(
)
(
)
, . .
II a a a h a h a a
= =
là dạng toàn phương cơ bản thứ hai có công thức dạng
(
)
(
)
(
)
2 2
2
u u v v
II a L a Ma a N a
= + + , với
, ,
L M N
được tính bởi
(
)
(
)
' , ' ,
u u
L n u v r u v
= - ,
(
)
(
)
(
)
(
)
' , ' , ' , ' ,
u v v u
M n u v r u v n u v r u v
= - = - ,
(
)
(
)
' , ' ,
v v
N n u v r u v
= - .
Nếu mặt
(
)
S
có tham số hóa dạng
(
)
(
)
(
)
(
)
(
)
, , , , , ,
r u v x u v y u v z u v
= thì
, ,
L M N
được tính
2
'' '' ''
1
' ' '
' ' '
uu uu uu
u u u
v v v
x y z
L x y z
EG F
x y z
=-,2
'' '' ''
1
' ' '
' ' '
uv uv uv
u u u
v v v
x y z
M x y z
EG F
x y z
=-,
2
'' '' ''
1
' ' '
' ' '
vv vv vv
u u u
v v v
x y z
N x y z
EG F
x y z
=-
11. Độ cong pháp dạng.
Lấy
(
)
: ' '
M u u v v
a T S a a r a r
Î = +
. Độ cong pháp dạng của
(
)
S
tại điểm
M
theo phương
a
được ký hiệu
(
)
M
K a
và
( ) ( )
( )
( ) ( )
( ) ( )
2 2
2 2
2
2
u u v v
M
u u v v
L a Ma a N a
II a
K a I a E a Fa a G a
+ +
= = + + .
Lưu ý.
(
)
(
)
M M
K a K a
l
=
12. Phương chính.
Giả sử
h
là ánh xạ Weingarten của mặt
(
)
S
,
(
)
, 0
M
a T S a
Î ¹
. Ta nói
a
là phương chính của
mặt
(
)
S
nếu
a
là véctơ riêng của ma trận ánh xạ tuyến tính
h
hay
(
)
h a a
l
= với
l
là độ cong
chính.
Thấy rằng
(
)
(
)
(
)
: ' , ' ,
M u u v v
a T S a a r u v a r u v
Î = +
ta sẽ xác định
,
u v
a a
dựa vào định thức
2 2
0
v u v u
a a a a
E F G
L M N
-
=
.
Khi đó
2
2
LN M
K
EG F
-
=
-
là độ cong Gauss,
( )
2
2
2
EN GL FM
HEG F
+ -
=- là độ cong trung bình.