- GVHD : Lê Ng c C ng ọ ườ
- L p HP ớ: 1016FMAT0211
M c l c:ụ ụ
Các d ng ph ng trình vi phân c p 1 và ví d .ạ ươ ấ ụ
•Ph ng trình vi phân c p 1 bi n s phân li.ươ ấ ế ố
• Ph ng trình vi phân có d ng y’= f(x).ươ ạ
• Ph ng trình đ ng c p c p 1.ươ ẳ ấ ấ
• Ph ng trình tuy n tính c p 1.ươ ế ấ
• Ph ng trình Bernoulli.ươ
Các d ng ph ng trình vi phân c p 2 và ví d .ạ ươ ấ ụ
•Ph ng trình vi phân c p 2 gi m c p đ c.ươ ấ ả ấ ượ
•Ph ng trình vi phân tuy n tính c p 2.ươ ế ấ
•Ph ng trình vi phân tuy n tính c p 2 h s ươ ế ấ ệ ố
h ng.ằ
ng d ng c a ph ng trình vi phân.Ứ ụ ủ ươ
• Mô hình ô nhi m môi tr ng.ễ ườ
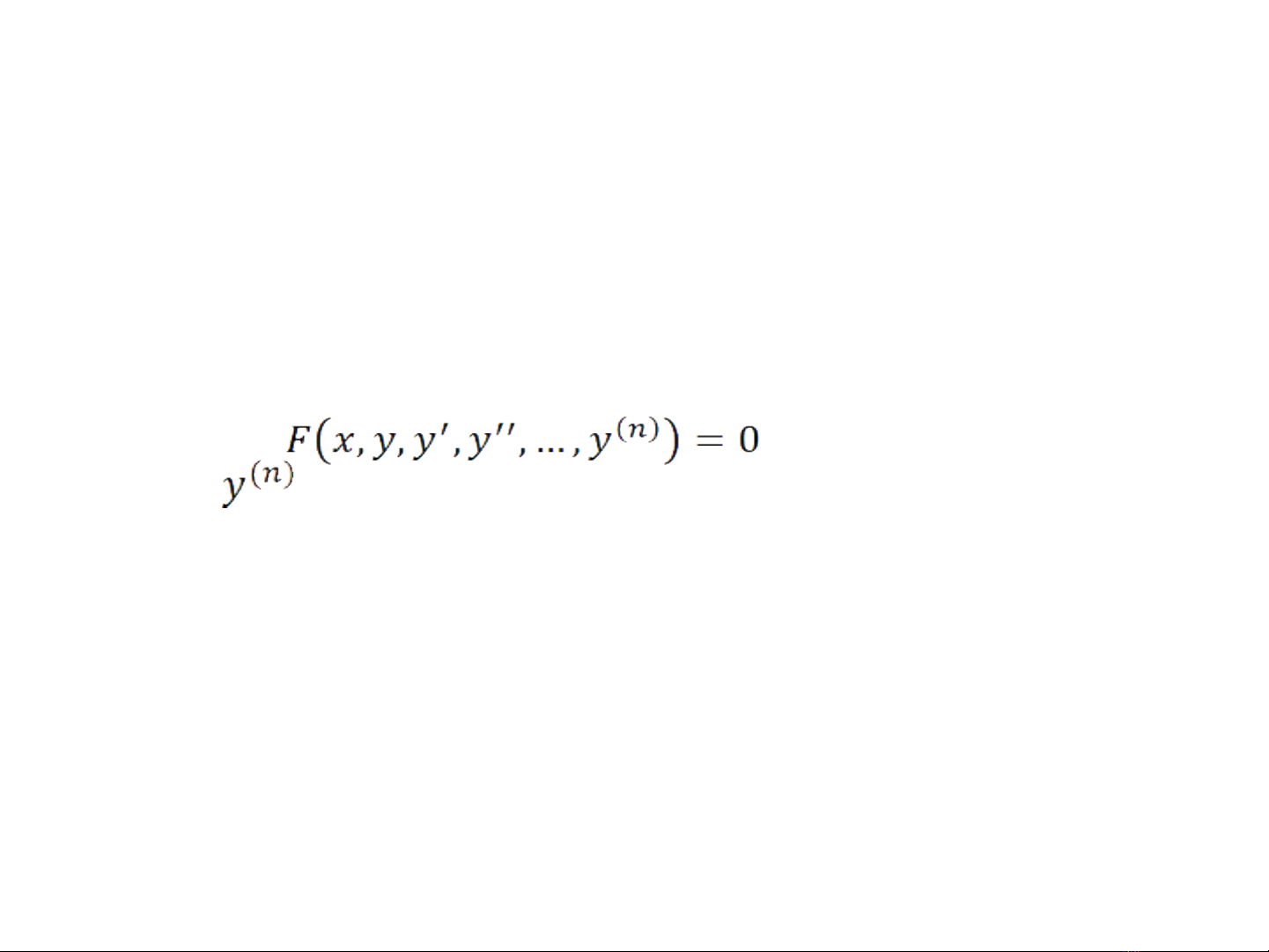
Các khái ni m c b n:ệ ơ ả
• Đ nh nghĩa: Ph ng trình vi phân là ph ng trình liên h ị ươ ươ ệ
gi a bi n đ c l p (hay các bi n đ c l p) hàm ch a bi t và ữ ế ộ ậ ế ộ ậ ư ế
đ o hàm c a hàm s đó.ạủố
• C p c a ph ng trình vi phân: là c p cao nh t c a đ o ấ ủ ươ ấ ấ ủ ạ
hàm c a hàm s có m t trong phuong trình đó.ủ ố ặ
-D ng t ng quát c a PTVP c p n v i bi n đ c l p x, bi n ph ạ ổ ủ ấ ớ ế ộ ậ ế ụ
thu c y là trong đó không đ c ộ ượ
khuy t .ế
• Nghi m c a ph ng trình vi phân: ệ ủ ư
Cho m t PTVP c p n, m i hàm s , kh bi n đ n c p n mà khi ộ ấ ọ ố ả ế ế ấ
thay vào ph ng trình đó cho ta đ ng nh t th c đ u g i là ươ ồ ấ ứ ề ọ
nghi m c a PTVP đó.ệ ủ
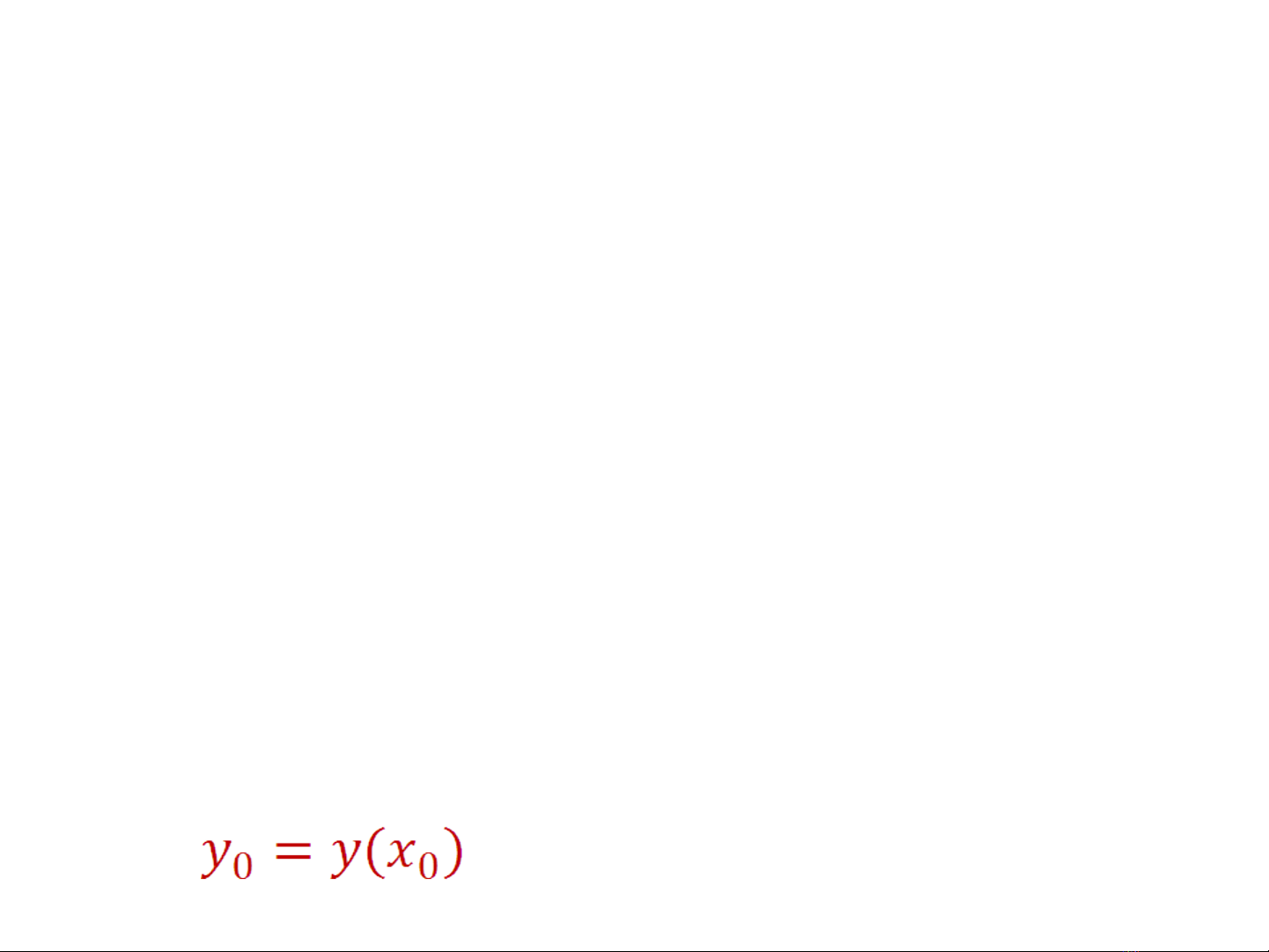
PH NG TRÌNH VI PHÂN C P 1ƯƠ Ấ
1.Đ nh nghĩa:ị
Ph ng trình vi phân c p 1 có d ng : ươ ấ ạ
+ D ng t ng quát ạ ổ F(x, y, y’) =0
+ D ng chính t cạ ắ y’= f(x)
2. Đ nh lí t n t i và duy nh t nghi mị ồ ạ ấ ệ :
- Cho PTVP c p 1:y’=f(x,y) n u f(x,y) liên t c trên mi n ấ ế ụ ề
m D v i Mo(xo,yo) D t n t i nghi m y=f(x) Th a mãn ở ớ ồ ạ ệ ỏ
yo=y(xo). N u f(x)liên t c trên D thìế ụ nghi m đó là duy ệ
nh t ấ
3.Đi u ki n ban đ u c a PTVP:ề ệ ầ ủ
∈
N u ế g i là đi u ki n ban đ uọ ề ệ ầ
∫∫
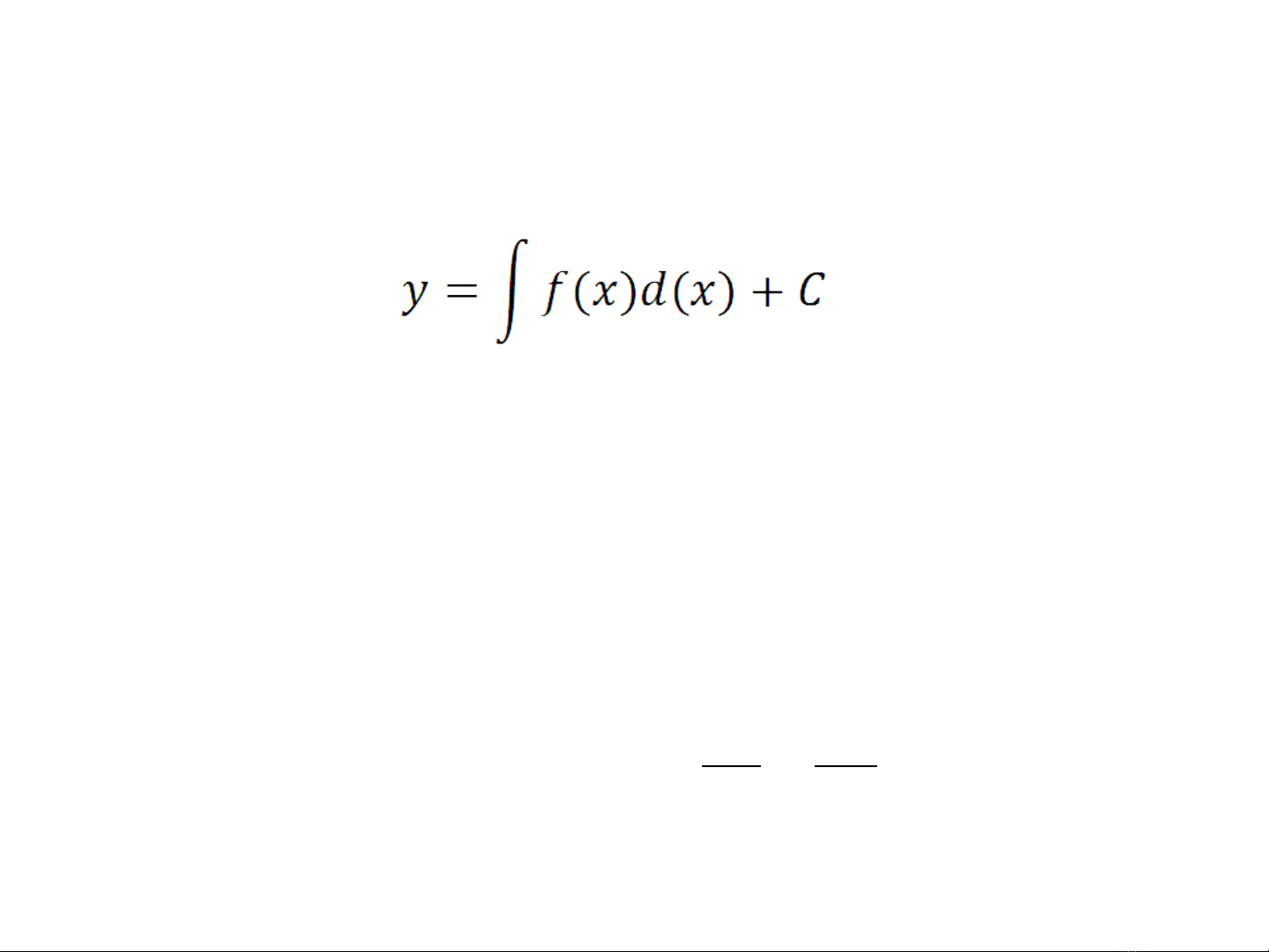
+= cdxxfdyyg )()(
2.2 Ph ng trình vi phân c p 1 bi n s phân li:ươ ấ ế ố
a. D ngạ: f(x)dx = g(y)dy
b. PP: tích phân 2 v ta đ cế ượ
0=+ ydyxdx
vd:
∫∫
=+ cydyxdx
c
y
x
=+⇒
22
2
2
cyx 2
22
=+⇒
là nghi m c a ph ng trình.ệ ủ ươ
tích phân 2 v ta đ cế ượ
2.1 Ph ng trình có d ng ươ ạ y’= f (x)
Ph ng pháp gi i: tích phân 2 v ta đ c ươ ả ế ượ
2.Các lo i ph ng trình vi phân c p 1 ạ ươ ấ