1
Chương 4: Tích phân số
Trường Đại Học Công Nghiệp Tp.HCM
Khoa Kỹ Thuật Cơ Khí
IUH - 2022
ThS. Hồ Thị Bạch Phương
Tích phân
2
Tích phân không xác định
Tích phân không xác định
khác nhau ở giá trị c.
c
x
dxx2
2
Tích phân xác định
Tích phân xác định là số cụ
thể.
2
1
2
1
0
1
0
2
x
xdx
Nếu f liên tục trên khoảng [a,b]. F là nguyên hàm của f
b
af(x)dx F(b) F(a)
3a b
f(x)
3210 xxxx
Khoảng [a,b] được chia thành các
khoảng nhỏ hơn.
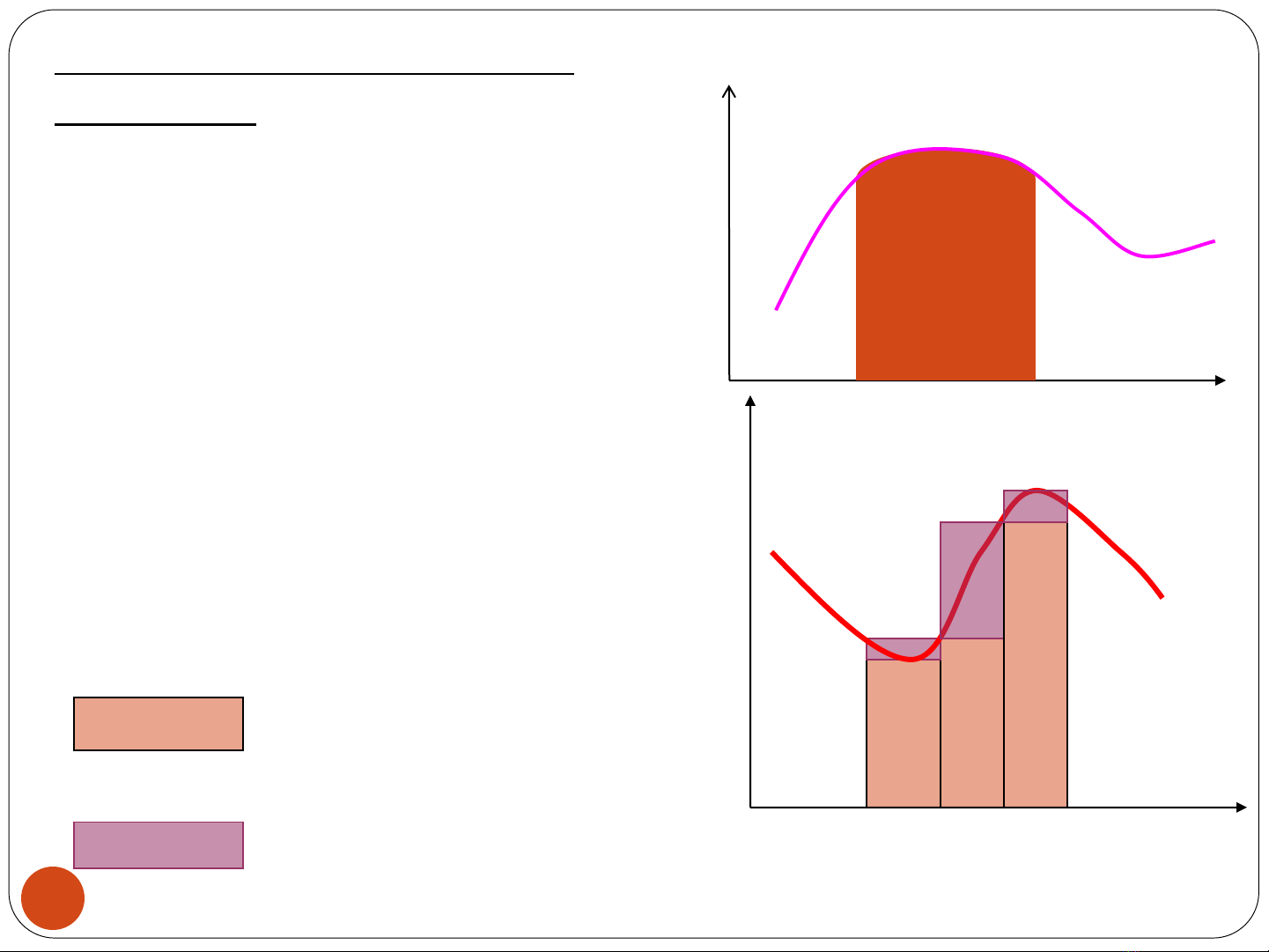
Công thức hình chữ nhật
Tích phân = diện tích (A) dưới
đường cong
b
a
A f(x)dx
f(x)
A
a b
0 1 2 n
P a x x x ... x b
i i i 1
i i i 1
m min f (x) : x x x
M max f (x) : x x x
Định nghĩa:
n1
i i 1 i
i0
n1
i i 1 i
i0
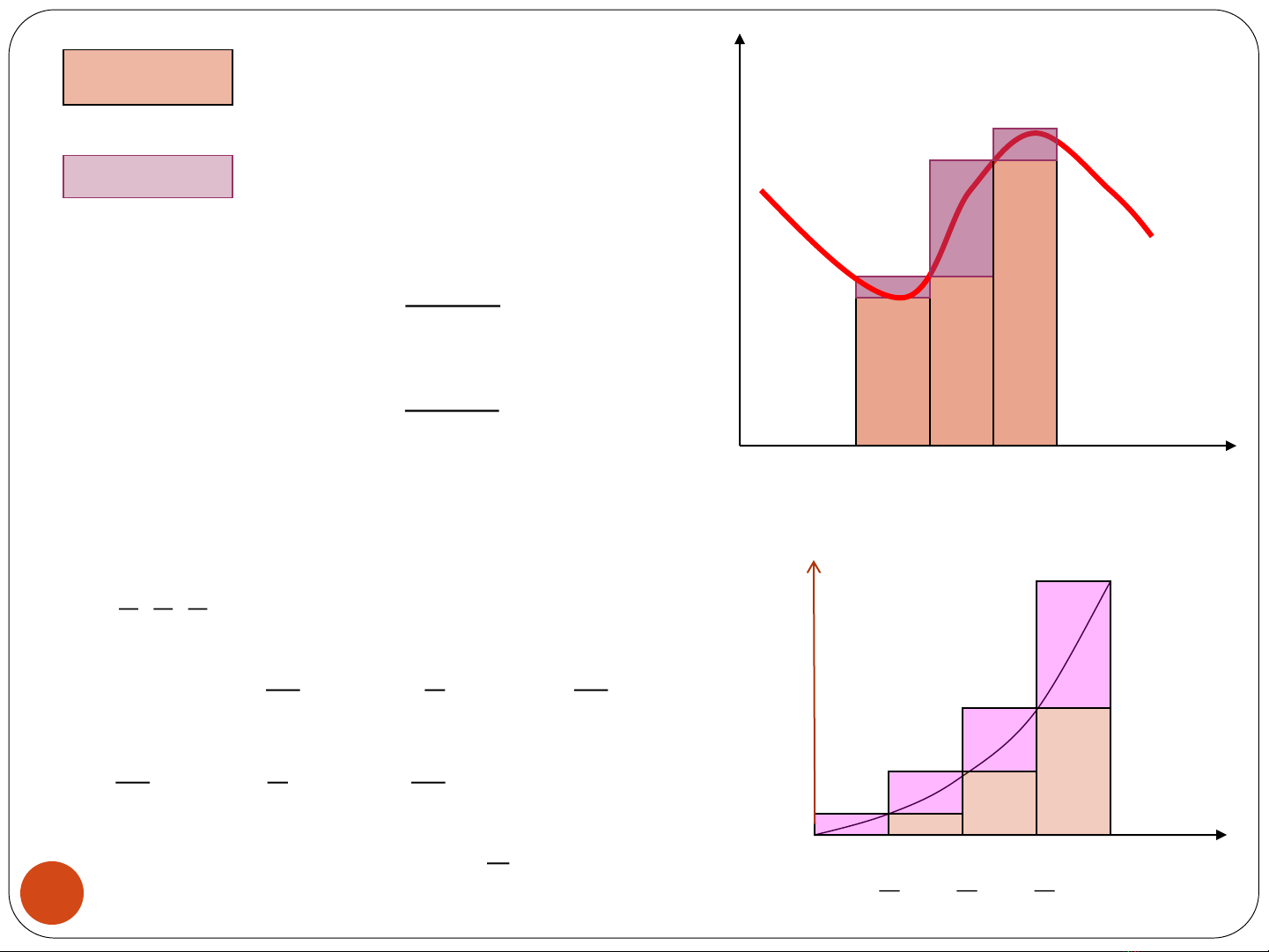
L(f ,P) m x x
U(f ,P) M x x
Tổng trên
Tổng dưới
ab
f(x)
3210 xxxx
LU
2
UL
2
1
4
3
2
1
4
1
0
i 1 i
1
x x cho i 0,1,2,3
4
Tổng trên
Tổng dưới
n1
i i 1 i
i0
n1
i i 1 i
i0
L(f ,P) m x x
U(f ,P) M x x
Ước tính tích phân
Sai số
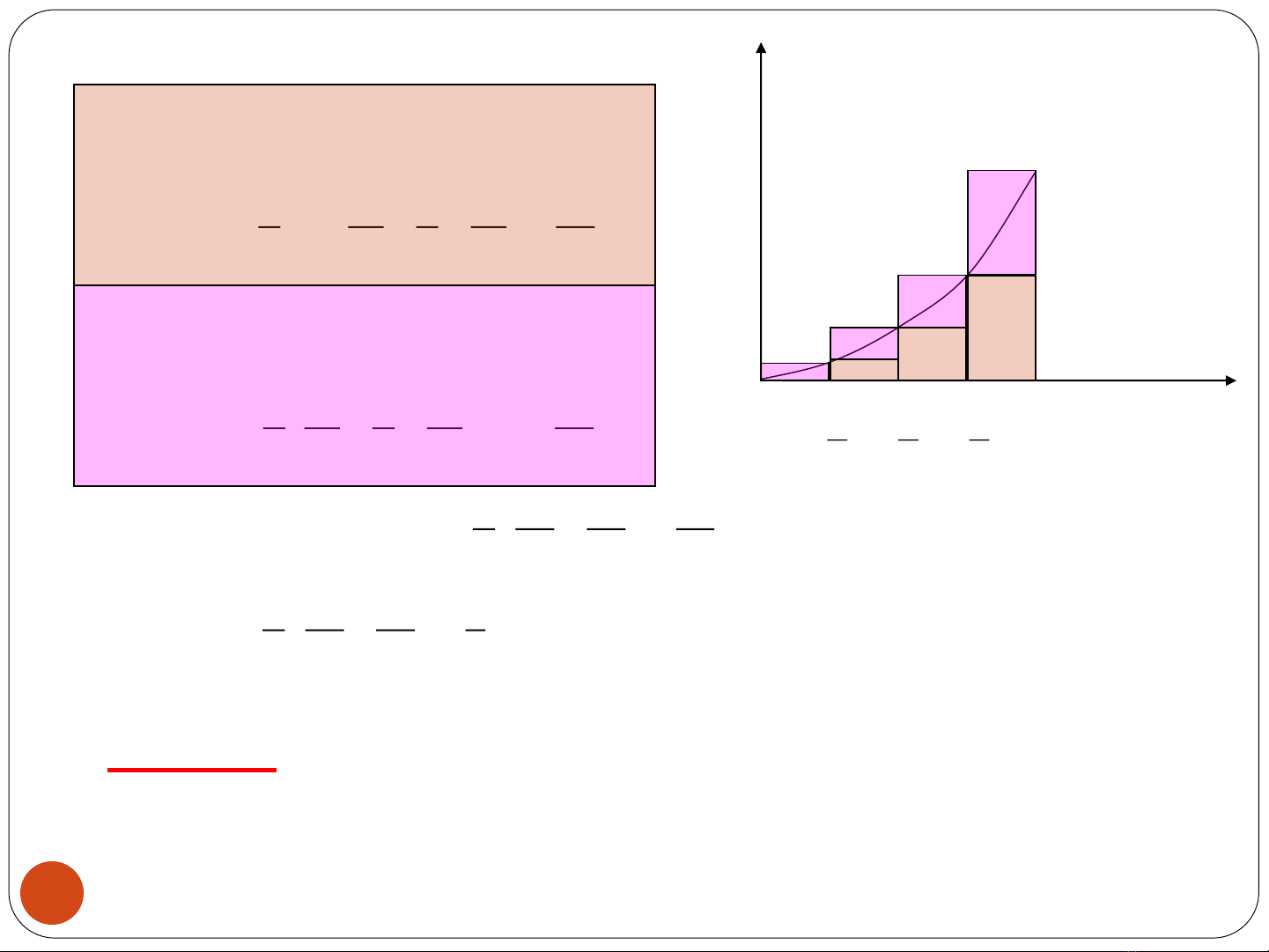
12
0x dx
1 2 3
P 0, , , ,1
444
n = 4: Chia 4 khoảng bằng nhau
0 1 2 3
0 1 2 3
1 1 9
m 0, m , m , m
16 4 16
1 1 9
M , M , M , M 1
16 4 16
TS. Lê T. P. Nam
4
Ví dụ 1:
5
1
4
3
2
1
4
1
0
n1
i i 1 i
i0
n1
i i 1 i
i0
L(f ,P) m x x
1 1 1 9 14
L(f ,P) 0
4 16 4 16 64
U(f ,P) M x x
1 1 1 9 30
U(f ,P) 1
4 16 4 16 64
1 30 14 11 0.34375
2 64 64 32
1 30 14 1
2 64 64 8
• Ước tính dựa trên tổng hình chữ nhật thì dễ để đạt cho hàm
đơn điệu (luôn luôn tăng hoặc luôn luôn giảm).
• Hàm không đơn điệu, tìm cực trị của hàm có thể khó khăn và
các phương pháp khác thì khả thi hơn.
Tổng trên
Tổng dưới
Ước tính tích phân
Sai số
