Trường Đại học Công nghiệp thành phố Hồ Chí Minh
Khoa Công nghệ Cơ khí
Bài 3:
Ứng dụng của Phương trình vi phân bậc I
Thời lượng: 2 tiết
Bộ môn Cơ sở - Thiết kế
1
Nội dung bài học 2
3
Ứng dụng của Phương trình vi phân bậc I
Gọi x(t) là số lượng của một đối tượng nào đó ở thời điểm t.
Giả sử rằng sự thay đổi số lượng này lại tỉ lệ thuận với chính số lượng đó ở
thời điểm đó. PTVP mô tả sự thay đổi này có dạng:
dx Kx
dt 
(1) –Trong đó K là hệ số tỉ lệ, là một hằng số
1 ln ln Kt
dx dx
K dt K dt x Kt C x C e
xx

Với điều kiện ban đầu: x(0) = x0, ta có C = x0
Vậy quy luật số lượng x(t) là:
0
Kt
x x e

(2)
(2) thể hiện số lượng của đối tượng tại bất kz một thời điểm t nào
4
Ứng dụng của Phương trình vi phân bậc I
0
Kt
x x e

(2)
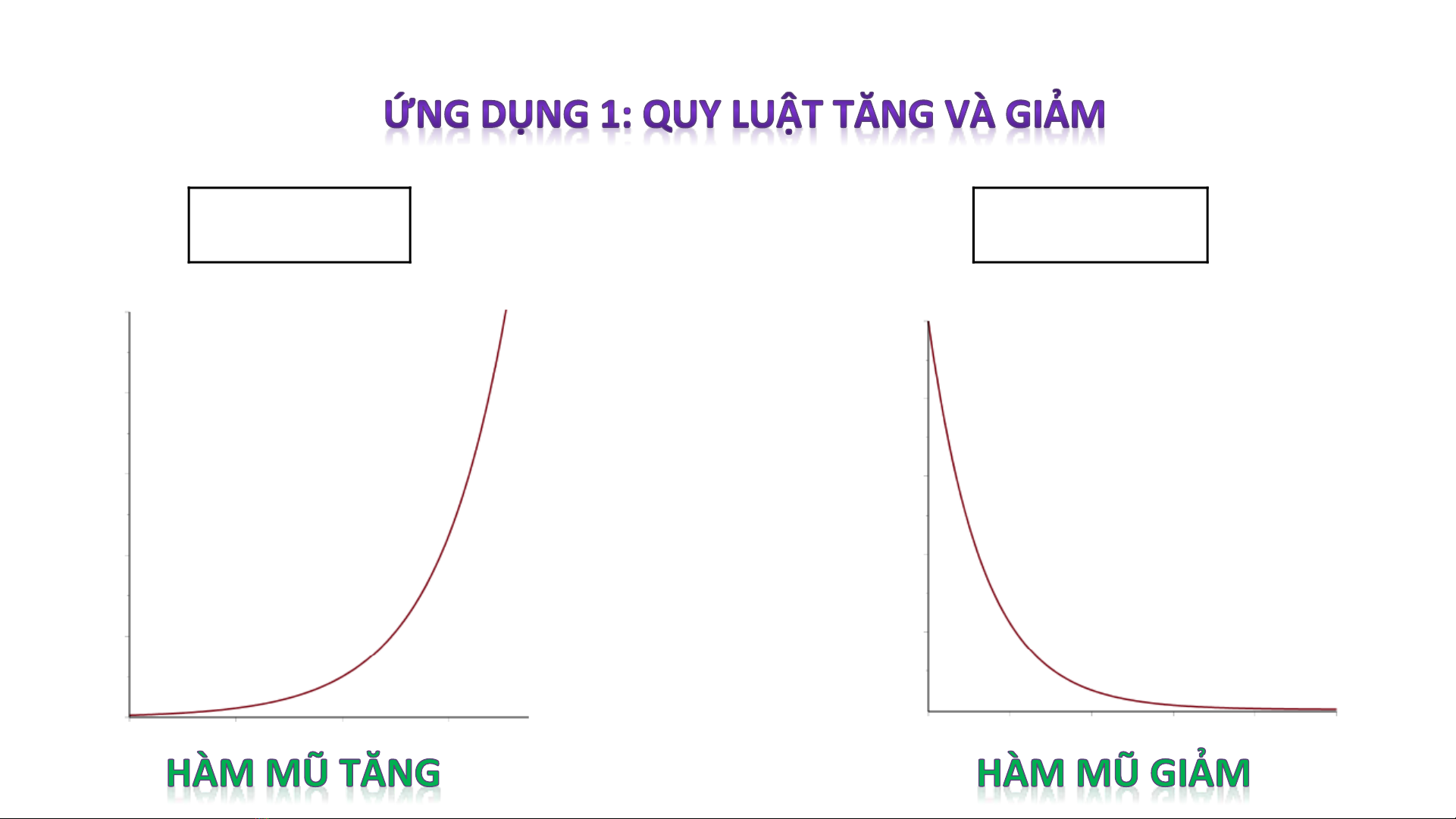
1) Nếu K>0, thì số lượng x sẽ tăng trưởng khi thời gian t tăng trong (2). PT (2)
thể hiện sự tăng trưởng tại bất kz thời điểm t nào. Sự tăng trưởng theo hàm
mũ.
Ví dụ: Số lượng vi khuẩn trong môi trường nuôi cấy phát triển theo cấp số
nhân trong điều kiện lý tưởng.
2) Nếu K<0, đặt K=–λ, λ>0, thì:
0
t
x x e


(3)
Có nghĩa là số lượng x sẽ giảm sút khi thời gian t tăng trong (3). PT (3) thể
hiện sự sụt giảm tại bất kz thời điểm t nào. Sự sụt giảm theo hàm mũ.
Ví dụ: thí nghiệm cho thấy rằng một chất phóng xạ bị phân hủy với tốc độ tỷ
lệ với lượng chất có mặt tại bất kz thời điểm nào.
5
Ứng dụng của Phương trình vi phân bậc I
0
Kt
x x e

0
t
x x e

