Trang 1
GIẢI BÀI TOÁN ĐIỆN XOAY CHIỀU DÙNG GIẢN ĐỒ VÉCTƠ
A. CÁCH VẼ GIẢN ĐỒ VÉC TƠ:
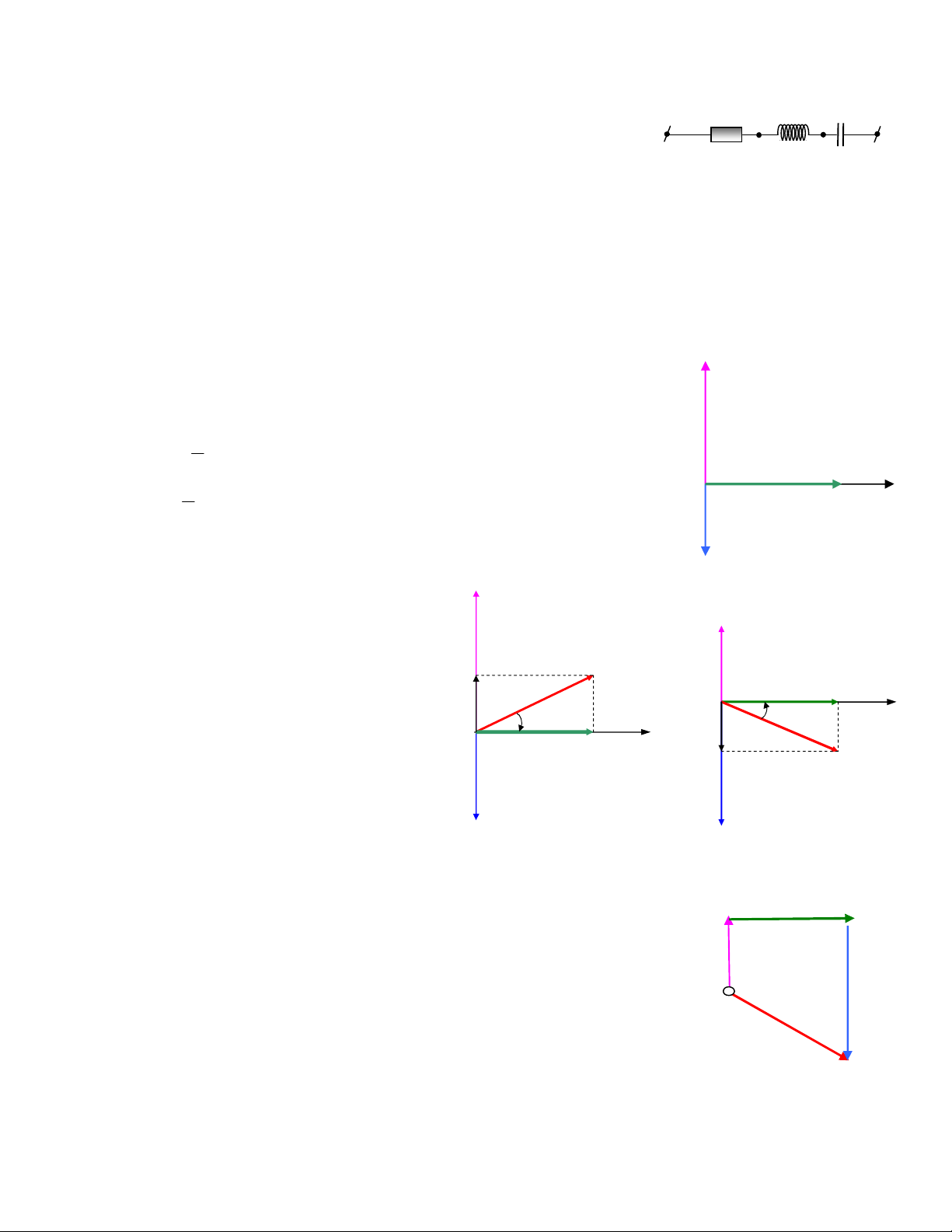
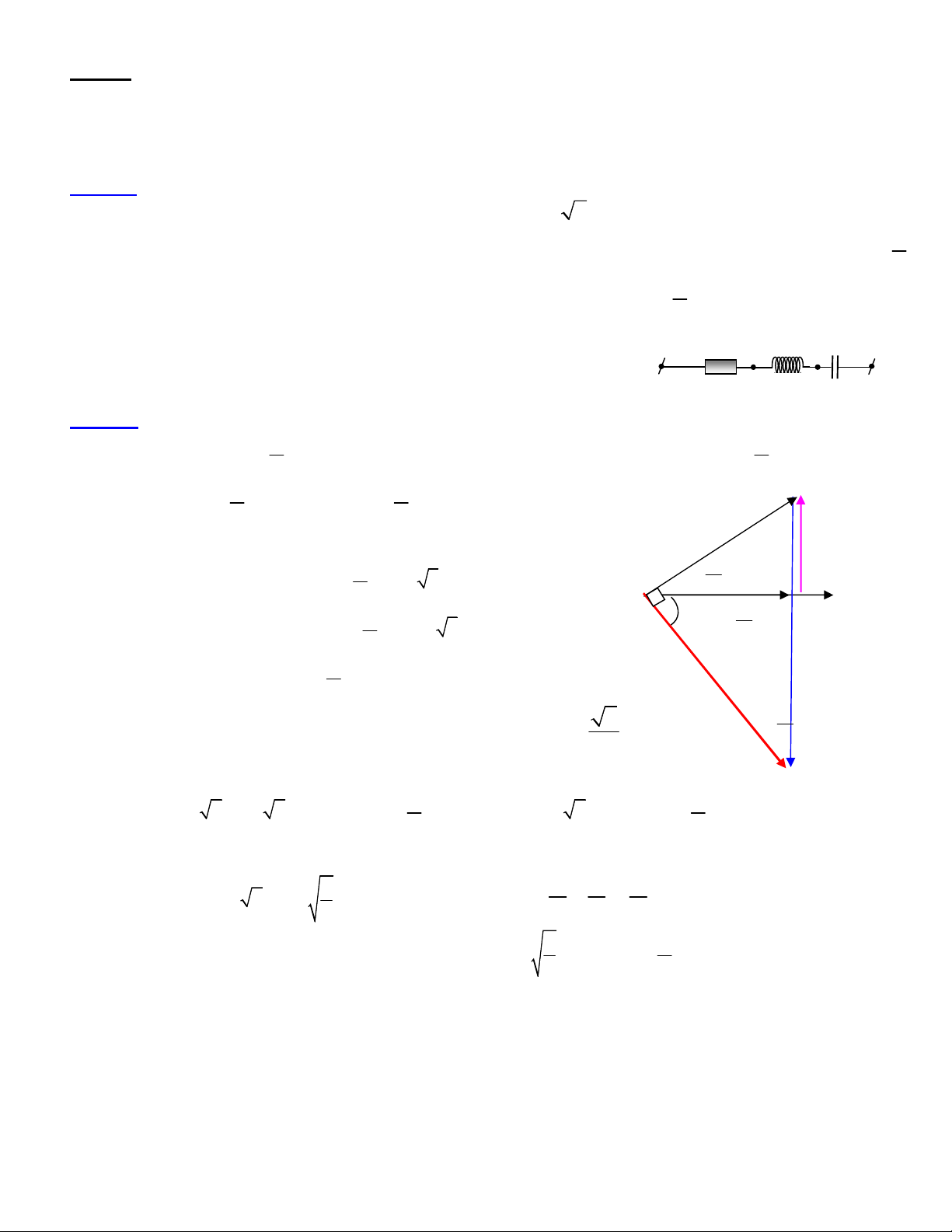
-Xét mạch R,L,C mắc nối tiếp như hình1.
Các giá trị tức thời của dòng điện là như nhau:
iR = iL = iC = i
Các giá trị tức thời của điện áp các phần tử là khác nhau và ta có:
u = uR +uL+uC
-Việc so sánh pha dao động giữa điện áp hai đầu mỗi phần tử với dòng điện chạy qua nó cũng chính là so sánh
pha dao động của chúng với dòng điện chạy trong mạch chính. Do đó trục pha trong giản đồ Frexnel ta chọn là
trục dòng điện thường nằm ngang. Các véc tơ biểu diễn các điện áp hai đầu mỗi phần tử và hai đầu mạch điện
biểu diễn trên trục pha thông qua quan hệ pha của nó với cường độ dòng điện.
1.Cách vẽ giản đồ véc tơ cùng gốc O :Véc tơ buộc(Qui tắc hình bình hành):
(Chiều dương ngược chiều kim đồng hồ)
-Ta có: ( xem hình 2)
+ uR cùng pha với i =>
R
U
cùng phương cùng chiều với trục i: Nằm ngang
+ uL nhanh pha
π
2
so với i =>
L
U
vuông góc với Trục i và hướng lên
+uC chậm pha
π
2
so với i =>
C
vuông góc với trục i và hướng xuống
-> Điện áp hai đầu đoạn mạch là: u = uR +uL + uC =>
C
U U U U
R L
Chung gốc O, rồi tổng hợp véc tơ lại!
(Như Sách Giáo khoa Vật Lý 12 CB)
-Để có một giản đồ véc tơ gọn ta không nên
dùng quy tắc hình bình hành (rối hơn hình 2b)
mà nên dùng quy tắc đa giác( dễ nhìn hình 3 ).
2.Cách vẽ giản đồ véc tơ theo quy tắc đa giác như hình 3 (Véc tơ trượt)
Xét tổng véc tơ:
C
U U U U
R L
Từ điểm ngọn của véc tơ
L
U
ta vẽ nối tiếp véc tơ
R
U
(gốc của
R
U
trùng với ngọn của
L
U
). Từ
ngọn của véc tơ
R
U
vẽ nối tiếp véc tơ
C
U
. Véc tơ tổng
U

có gốc
là gốc của
L
U
và có ngọn là ngọn của véc tơ cuối cùng
C
U
(Hình 3)
L - lên.; C – xuống.; R – ngang.
Vận dụng quy tắc vẽ này ta bắt đầu vẽ giản đồ véc tơ
cho bài toán mạch điện xoay chiều như sau!.
L
U
R
U
I
C
U
Hình 2
L
U
R
U
C
U
U
Hình 3
C
A B
R L
Hình
1
O
L
U
C
U
LC
U
R
U
U
I
O
L
U
C
U
LC
U
R
U
U
I
Hình 2b
Trang 2
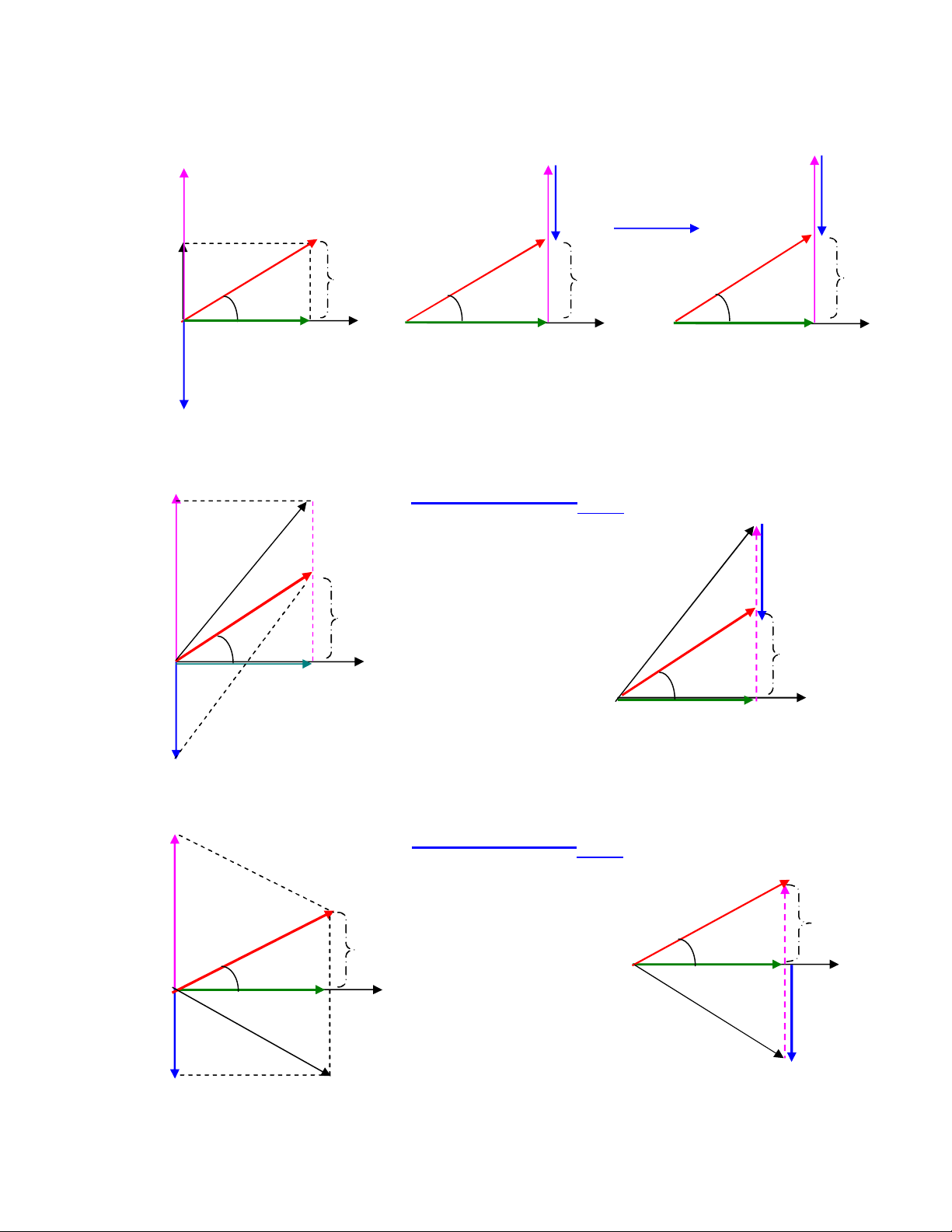
B. Một số Trường hợp thường gặp:
1. Trường hợp 1: UL > UC <=> > 0 u sớm pha hơn i
- Phương pháp véc tơ trượt ( Đa giác): Đầu tiên vẽ véc tơ
R
U

, tiếp đến là
L
U

cuối cùng là
C
U

. Nối
gốc của
R
U
với ngọn của
U
C

ta được véc tơ
U
như hình sau:
Khi cần biểu diễn
RL
U
Khi cần biểu diễn
RC
U
U
L
-
U
C
L
U
R
U
U
C
U
LC L C
U U U
Vẽ theo quy tắc hình bình hành(véc tơ buộc)
C
U
L
U
R
U
RC
U
U
U
L
-
U
C
Vẽ theo quy tắc hình bình hành
U
L
-
U
C
L
U
R
U
U
C
U
RC
U
Vẽ theo quy tắc đa giác
Vẽ theo quy tắc đa giác
U
L
-
U
C
L
U
R
U
RL
U
U
C
U
C
U
L
U
R
U
RL
U
U
U
L
-
U
C
Vẽ theo quy tắc hình bình hành
ZL - ZC
L
Z
Z

I
C
Z
R
đa giác tổng trở
C
Z R Z Z
L
U
L
-
U
C
L
U
U

I
C
U
R
U
Vẽ theo quy tắc đa giác ( dễ nhìn)
Trang 3
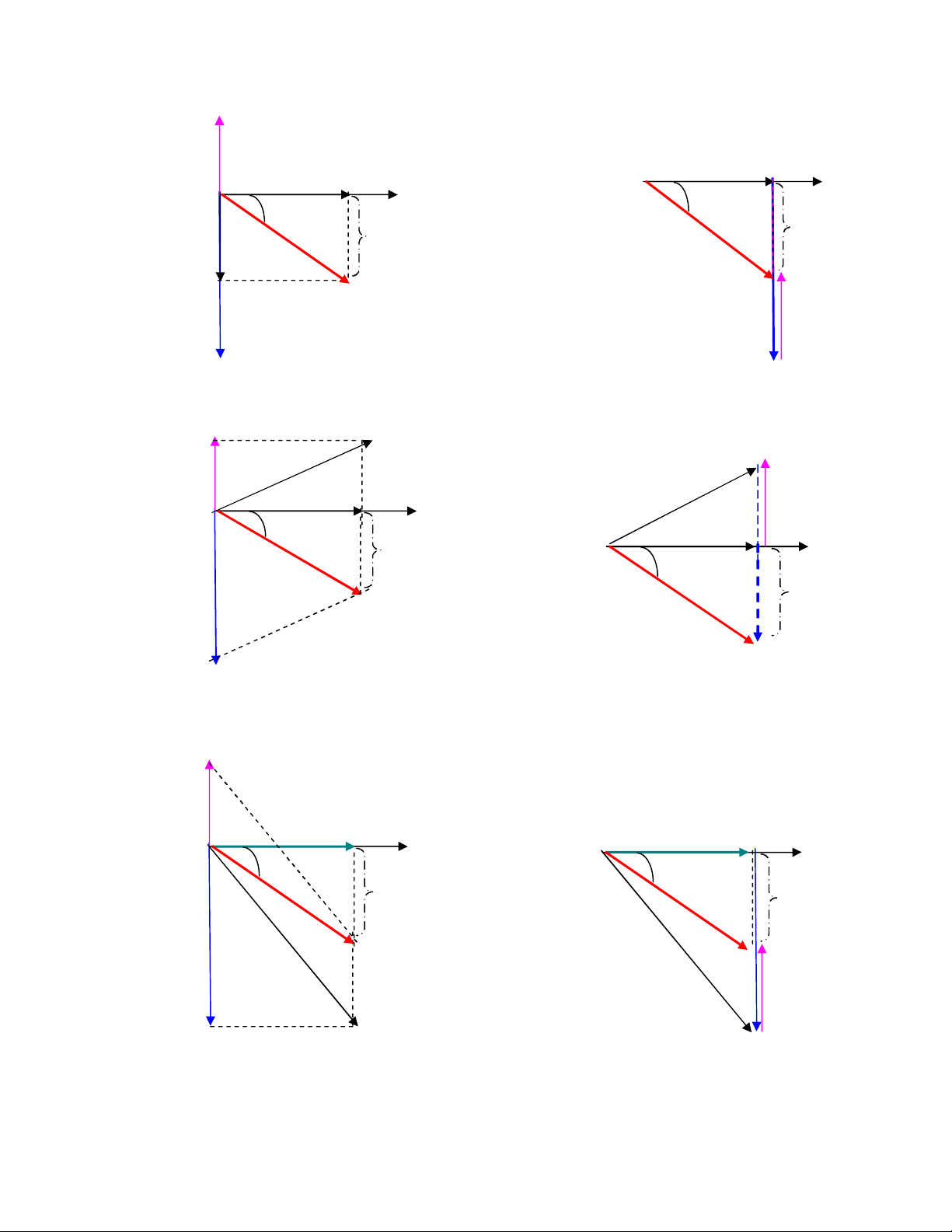
2. Trường hợp 2: UL < UC <=> < 0: u trễ pha so với i ( hay i sớm pha hơn u )
Làm lần lượt như trường hợp 1 ta được các giản đồ thu gọn tương ứng là
L
U
R
U
C
U
U
U
L
-
U
C
L
U
R
U
C
U
U
LC L C
U U U
U
L
-
U
C
L
U
R
U
C
U
U
UL - UC
RL
U
L
U
R
U
C
U
U
UL - UC
RL
U
L
U
R
U
C
U
U
UL - UC
RC
U
L
U
R
U
C
U
U
RC
U
Trang 4
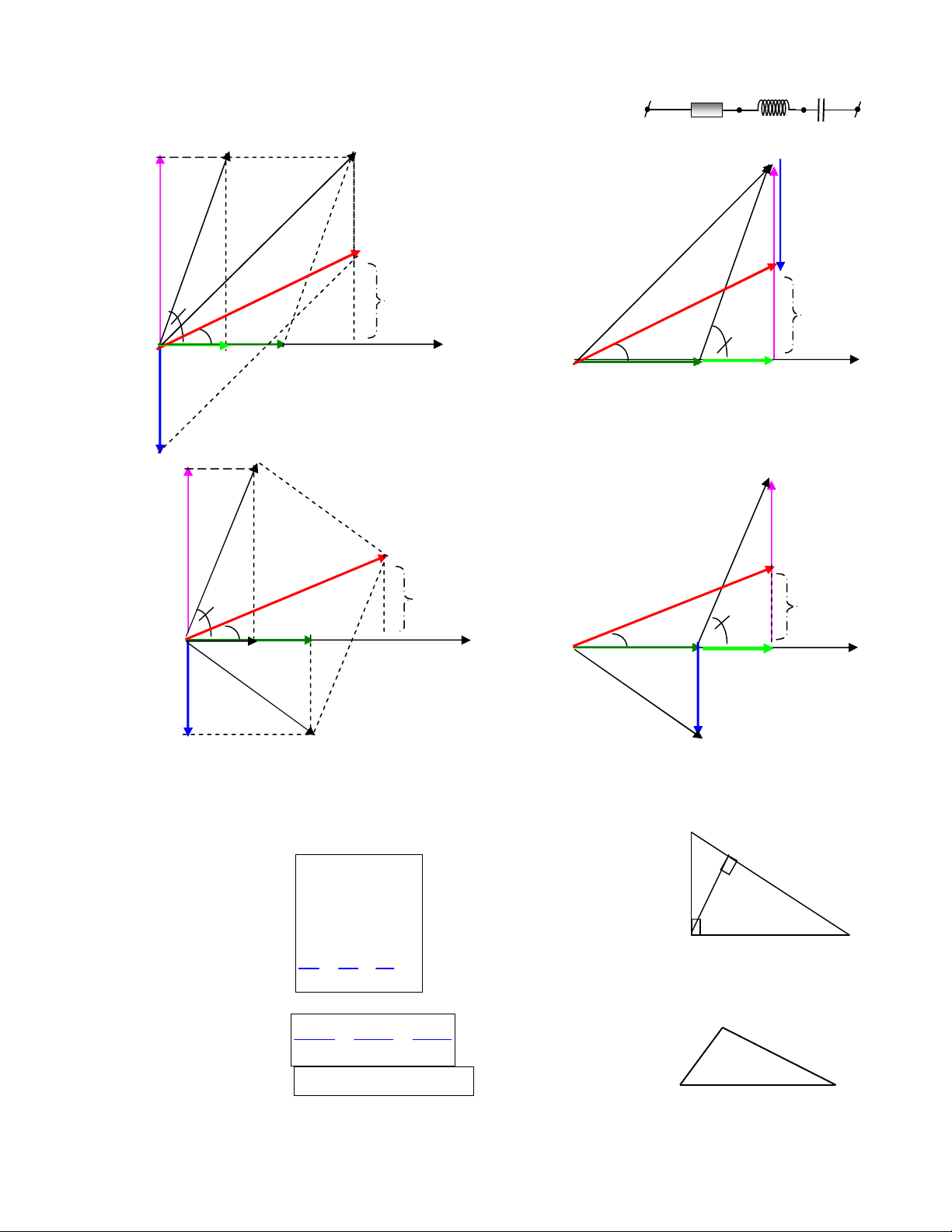
3. Trường hợp đặc biệt - Cuộn cảm có điện trở thuần r
Vẽ theo đúng quy tắc và lần lượt từ
R
U
, đến
Ur
, đến
L

, đến
C
U
C. Một số công thức toán học thường áp dụng :
1. Hệ thức lượng trong tam giác vuông: Cho tam giác vuông ABC
vuông tại A đường cao AH = h, BC = b, AC = b, AB = c, CH = b,, BH = c, ta
có hệ thức sau:
2 , 2 ,
2 , ,
2 2 2
b ab ;c ac
h b c
b.c a.h
1 1 1
h b c
2. hệ thức lượng trong tam giac:
a. Định lý hàm số sin:
a b c
sin A sin B sin C
b. Định lý hàm số cos:
2 2 2
a b c 2bccos A
d
U
L
U
R
U
Rd
U
U
UL - UC
d
r
U
C
U
UL - UC
d
U
L
U
R
U
Rd
U
U
d
r
U

C
U
d
U
L
U
R
U
U
UL - UC
d
RC
U
r
U
C
U
RC
U
d
U
L
U
R
U
U
UL - UC
d
r
U
C
U
B
C
A R L,r N
m
M
h
A
B
C
H
a
b
c
b
’
c
'
A
B
C
a
b
c
Trang 5
Chú ý: Thực ra không thể có một giản đồ chuẩn cho tất cả các bài toán điện xoay chiều nhưng những giản đồ
được vẽ trên là giản đồ có thể thường dùng . Việc sử dụng giản đồ véc tơ nào là hợp lí còn phụ thuộc vào kinh
nghiệm của từng người. Dưới đây là một số bài tập có sử dụng giản đồ véc tơ làm ví dụ.
D.CÁC VÍ DỤ ĐIỂN HÌNH.
Ví dụ 1.Cho mạch điện xoay chiều như hình vẽ, cuộn dây thuần cảm có độ tự cảm L, tụ điện có điện dung C,
điện trở có giá trị R. Hai đầu A, B duy trì một điện áp u =
100 2 cos100 (V )
t
.Cường độ dòng điện chạy
trong mạch có giá trị hiệu dụng là; 0,5A. Biết điện áp giữa hai điểm A,M sớm pha hơn dòng điện một góc
6
Rad; Điện áp giữa hai điểm M và B chậm pha hơn điện áp giữa A và B một góc
6
Rad
a. Tìm R,C?
b. Viết biểu thức cường độ dòng điện trong mạch?
c. Viết biểu thức điện áp giữa hai điểm A và M?
Lời giải:Chọn trục dòng điện làm trục pha
Theo bài ra uAM sớm pha
6
so với cường độ dòng điện. uMB chậm pha hơn uAB một góc
6
, mà uMB lại chậm
pha so với i một góc
2
nên uAB chậm pha
3
so với dòng điện.
Vậy ta có giản đồ vecto sau biểu diện phương trình:
AB AM MB
U U U

Từ giãn đồ vec to ta có:UAM = UAB.tg
6
=100/
3
(V)
UMB = UC = UAM/sin
6
= 200/
3
(V)
UR = UAM.cos
6
= 50 (V)
a. Tìm R,C? R = UR/I = 50/0,5 = 100
; C =
-4
C C
3
1/
ω Z =I/ω U = .10 F
4
π
b. Viết phương trình i? i = I0cos(100
πt
+
i
)
Trong đó: I0 = I.
2
=0,5
2
(A);
i
=-
=
3
(Rad). Vậy i = 0,5
2
cos(100
πt
+
3
) (A)
c.Viết phương trình uAM? uAM = u0AMcos(100
πt
+
AM
)
Trong đó: U0AM =UAM
2
=100
2
3
(V);
AM
=
6 3 2
AM
u i i
(Rad).
Vậy : biểu thức điện áp giữa hai điểm A và M: uAM = 100
2
3
cos(100
πt
+
2
)(V)
Kinh nghiệm:
1. khi vẽ giản đồ véc tơ cần chỉ rỏ: Giản đồ vẽ cho phương trình điện áp nào? Các véc tơ thành phần lệch
pha so với trục dòng điện những góc bằng bao nhiêu?
2. Khi viết phương trình dòng điện và điện áp cần lưu ý:
được định nghĩa là góc lệch pha của u đối
với i do vậy thực chất ta có:
=
u -
i suy ra ta có:
u=
+
i (1*)
UL - UC
L
U
R
U
C MB
U U
3
U
AB
AM
U
6
6
C
A B
R L
M