285
MỘT SỐ BÀI TOÁN THỰC TẾ LIÊN QUAN ĐẾN HÌNH CHỮ NHẬT
Lê Nguyễn Hạnh Nguyên 1; Trần Thanh Phong2
1. Lớp D20GDTH07, Trường Đại học Thủ Dầu Một
2. Khoa Sư phạm, Trường Đại học Thủ Dầu Một
TÓM TẮT
Theo chương trình giáo dục phổ thông môn toán về mục tiêu cấp Tiểu học giúp học sinh có
những kiến thức và kỹ năng toán học cơ bản ban đầu thiết yếu về số và phép tính, Hình học và Đo
lường, Thống kê và Xác suất. Phần Hình học và Đo lường ở bậc Tiểu học giúp học sinh quan sát,
nhận biết, mô tả hình dạng và đặc điểm (ở mức độ trực quan) của một số hình phẳng và hình khối
trong thực tiễn; tạo lập một số mô hình hình học đơn giản; tính toán một số đại lượng hình học; phát
triển trí tưởng tượng không gian; giải quyết một số vấn đề thực tế đơn giản gắn với Hình học và Đo
lường (với các đại lượng đo thông dụng). Hình học góp phần phát triển trí tưởng tượng cho học sinh,
phát triển năng lực tư duy, phát huy khả năng áp dụng kiến thức hình học vào thực tế cuộc sống.
Trong bài viết này, chúng tôi trình bày nội dung hình chữ nhật ở bậc tiểu học và một số bài toán thực
tế liên quan đến hình chữ nhật.
Từ khóa: Hình chữ nhật, bài toán thực tế, hình học và đo lường.
1. ĐẶT VẤN ĐỀ
Toán học là một môn học quan trọng và có vai trò to lớn trong việc phát tư duy, trí tuệ, phát
triển kỹ năng logic và sáng tạo. Cùng với sự đổi mới trong giáo dục Tiểu học về nội dung và phương
pháp dạy học mà trong đó các bài toán thực tế được quan tâm.
Việc áp dụng lồng ghép những bài toán thực tế vào dạy học toán cho học sinh Tiểu học là rất
cần thiết, nhằm gây hứng thú và tăng khả năng tư duy của học sinh. Nếu các em được tiếp xúc càng
sớm và càng nhiều với các bài toán thực tế sẽ giúp trí não được phát triển sớm hơn và vận dụng được
tối đa, giúp có một nền kiến thức sâu và vững chắc.
Trong dạy học, nếu giáo viên biết cách sáng tạo, linh hoạt tùy thuộc vào nội dung để tạo tình
huống, thiết kế nội dung dạy học với nhiều bài toán thực tế hấp dẫn thì từ đó sẽ thu hút và giúp học
sinh hứng thú hơn.
2. PHƯƠNG PHÁP NGHIÊN CỨU
Nghiên cứu chương trình giáo dục phổ thông toán năm 2018, các tài liệu; thảo luận với giảng
viên toán học và các bạn; sử dụng các phương pháp cơ bản của toán học như là phân tích tổng hợp
quy nạp toán học. Từ đó, chúng tôi xây dựng một số bài toán kèm theo lời giải chi tiết.
3. NỘI DUNG
3.1. Hình chữ nhật trong bậc học Tiểu học
3.1.1. Định nghĩa hình chữ nhật
Hình chữ nhật có 4 đỉnh, 4 góc vuông, 2 cạnh dài có độ dài bằng nhau và 2 cạnh ngắn có độ dài
bằng nhau.
Độ dài cạnh dài gọi là chiều dài, độ dài cạnh ngắn gọi là chiều rộng.
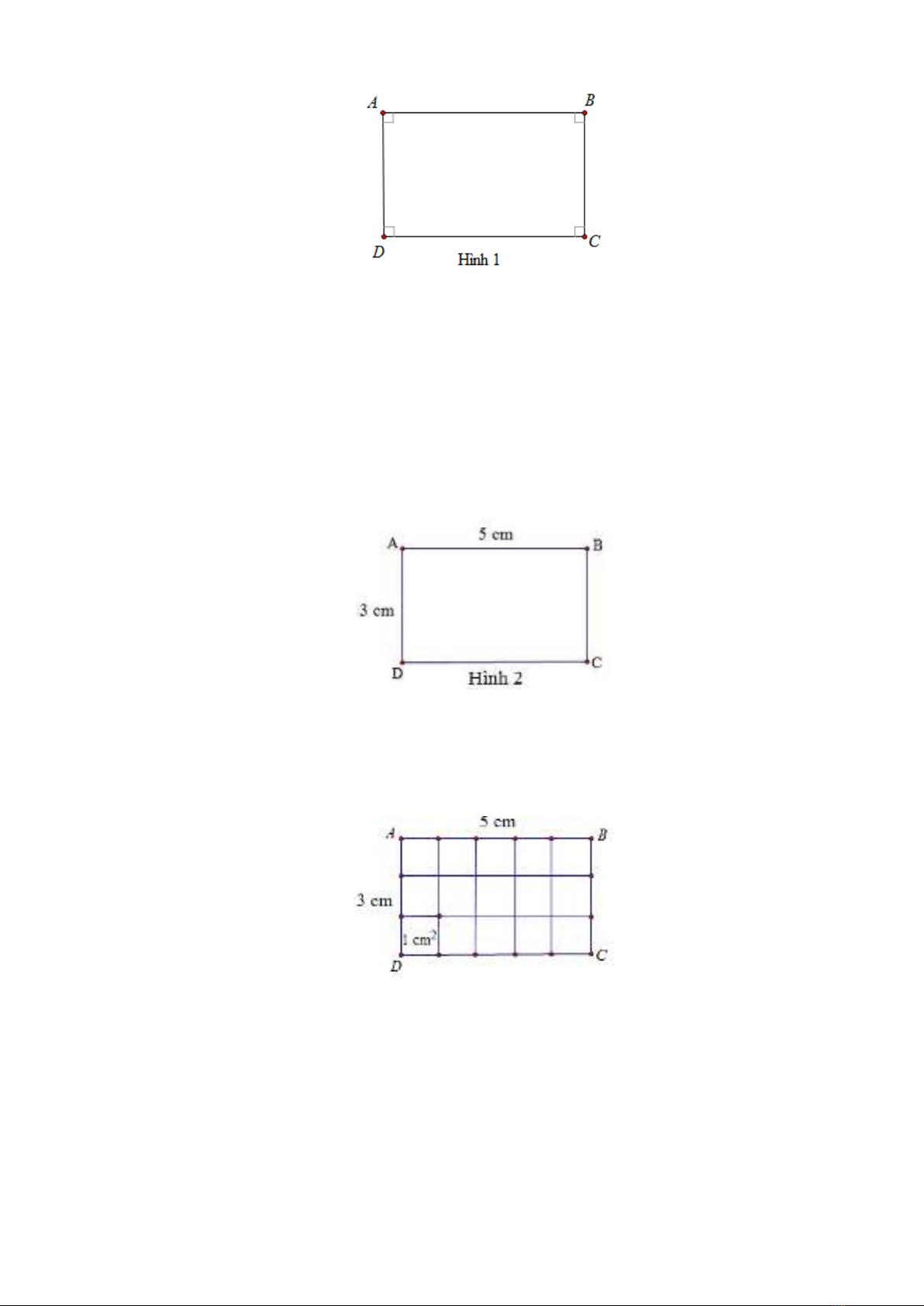
286
Hình chữ nhật ABCD (Hình 1) có:
4 đỉnh, 4 cạnh và 4 góc vuông;
2 cạnh dài AB và DC có độ dài bằng nhau, viết là AB = DC. Hai cạnh ngắn AD và BC có độ
dài bằng nhau, viết là AB = BC.
Ta cũng có thể bắt gặp rất nhiều hình chữ nhật trong cuộc sống hằng ngày: bảng đen là hình chữ
nhật, mặt bàn là hình chữ nhật, quyển vở là hình chữ nhật, tivi có hình chữ nhật,…
3.1.2. Công thức chu vi hình chữ nhật
Muốn tính chu vi hình chữ nhật ta lấy chiều dài cộng với chiều rộng (cùng đơn vị đo) rồi nhân
với 2.
Giả sử cho hình chữ nhật ABCD (hình 2):
Chu vi hình chữ nhật ABCD là:
5+3+5+3 = 16 (cm).
Hoặc (5+3) x 2 = 16 (cm).
3.1.2. Công thức diện tích hình chữ nhật
Muốn tính diện tích hình chữ nhật ta lấy chiều dài nhân với chiều rộng (cùng đơn vị đo).
Hình 3
Hình chữ nhật ABCD (Hình 3) có:
4 x 3 = 12 (ô vuông).
Diện tích mỗi ô vuông là 1cm2.
Diện tích hình chữ nhật ABCD là:
4 x 3 = 12 (cm2).
3.1.2. Liên hệ với hình chữ nhật trong thực tế
Trong cuộc sống hằng ngày học sinh được tiếp xúc với rất nhiều hình chữ nhật với mọi kích
thước khác nhau như mặt bàn, tivi, tủ lạnh, hộp đựng khăn giấy, máy tính,…
287
Ứng dụng của hình chữ nhật trong thực tế: Hình chữ nhật là một hình học có các đặc điểm đối
xứng và góc vuông, nên có rất nhiều ứng dụng trong thực tế. Dưới đây là một vài ứng dụng của hình
chữ nhật:
Kiến trúc: Hình chữ nhật được sử dụng rộng rãi trong kiến trúc. Nhiều công trình như nhà ở,
toà nhà, và cầu đường được thiết kế dựa trên hình dáng chữ nhật.
Công nghệ: Trong công nghệ, hình chữ nhật được sử dụng để thiết kế các công cụ, thiết bị và
máy móc. Ví dụ, màn hình máy tính, bàn phím, và hộp đựng thiết bị điện tử thường có hình dạng chữ
nhật.
Thương mại: Hình chữ nhật cũng được sử dụng trong lĩnh vực kinh doanh và thương mại. Ví
dụ, các cửa hàng và siêu thị thường sử dụng giá kệ hình chữ nhật để trưng bày hàng hóa. Hình dáng
chữ nhật cũng được sử dụng trong việc thiết kế các bảng hiệu quảng cáo.
Nông nghiệp: Trên mảnh đất hình chữ nhật, người ta thường trồng và chăm sóc cây trồng
hoặc nuôi động vật. Hình chữ nhật giúp tối ưu hóa sự sắp xếp và quản lý các hoạt động nông nghiệp.
Học tập: Hình chữ nhật cũng được sử dụng trong giảng dạy và học tập. Học sinh thường học
về tính chất và công thức tính diện tích và chu vi của hình chữ nhật trong môn toán. Đó là một số ứng
dụng cơ bản của hình chữ nhật trong thực tế. Tuy nhiên, hình chữ nhật còn được sử dụng rộng rãi
trong nhiều lĩnh vực khác nhau nhờ tính đa dạng và tính ứng dụng của nó.
3.2. Một số bài toán thực tế liên quan đến hình chữ nhật trong chương trình tiểu học
3.2.1. Dạng toán nhận biết hình chữ nhật
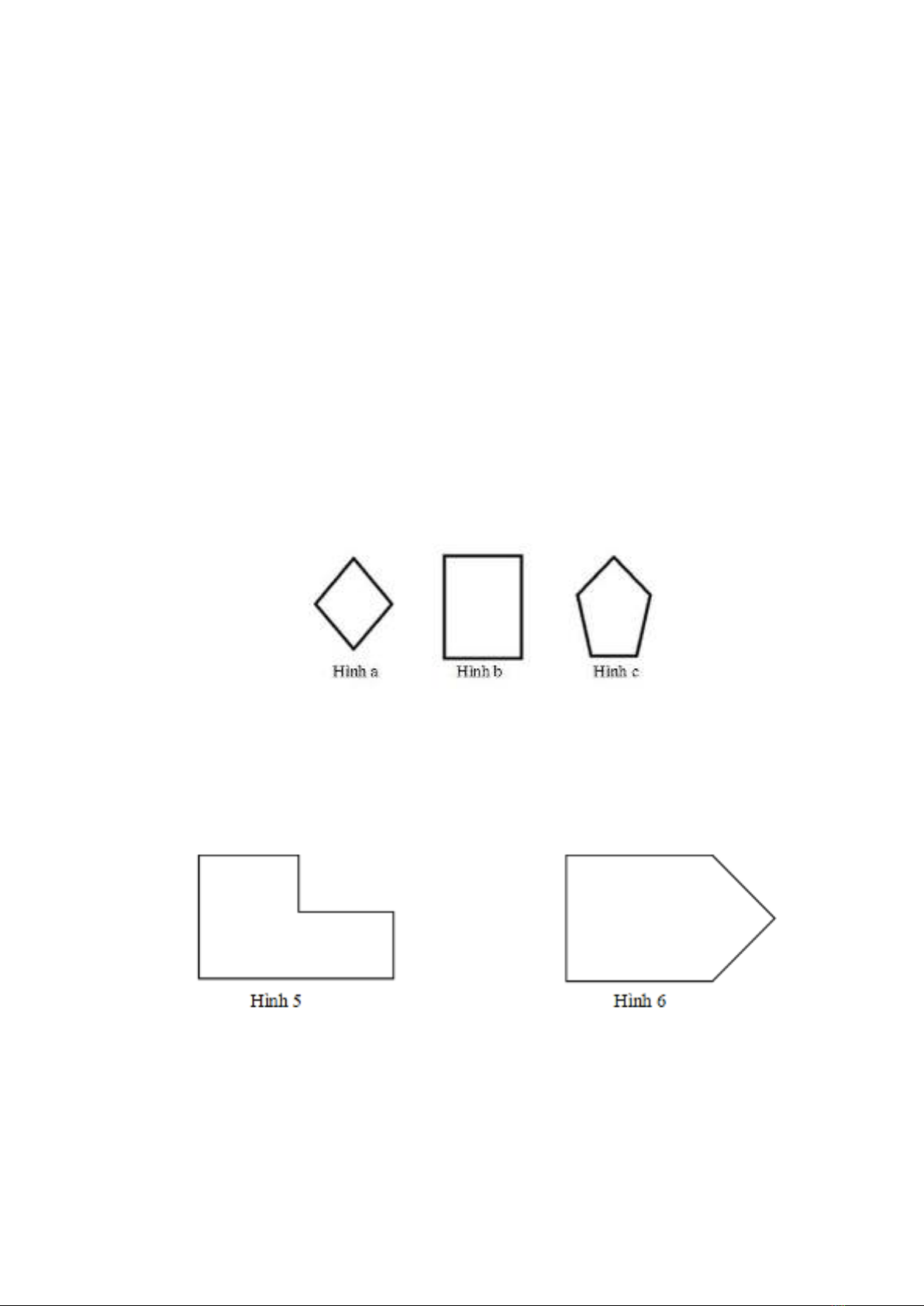
Bài 1. Hình nào là hình chữ nhật? (Hình 4)
Hình 4
A. Hình a
B. Hình b
C. Hình c
Hướng dẫn: Nhìn vào bài toán dễ dàng nhận ra hình b chính là hình chữ nhật.
Bài 2. Kẻ thêm đoạn thẳng để được hình chữ nhật (Hình 5, Hình 6).
Hướng dẫn: Sử dụng thước đo rồi kẻ sao cho 4 góc đều là 90 độ, có đủ chiều dài và chiều rộng.
Sau khi kẻ sẽ được hình chữ nhật sau đây (Hình 7, Hình 8)
288
Bài 3: Có tất cả bao nhiêu hình chữ nhật trong hình sau (Hình 9):
Hình 9
Hướng dẫn: Có 3 hình chữ nhật.
3.2.2. Dạng toán nhận biết hình chữ nhật dựa trên các đặc điểm về cạnh
Bài 4. Nhà các bạn sâu vẽ bùa, sâu xám, sâu khoang và sâu tơ ở bốn đỉnh của hình chữ nhật
ABCD (Hình 10). Biết rằng BC = 12dm, CD = 20dm.
a) Nhà sâu vẽ bùa cách sâu tơ bao nhiêu đề-xi-mét?
b) Nhà sâu vẽ bùa cách sâu xám bao nhiêu đề-xi-mét?
289
Hình 10
Hướng dẫn: Với bài tập này, học sinh cần xác định các độ dài đề bài yêu cầu tính ở câu a và b
là độ dài cạnh nào của hình chữ nhật, sau đó dựa vào đặc điểm về cạnh của hình chữ nhật liên hệ với
các cạnh đã biết, để tìm ra đáp số.
Gợi mở bằng một số câu hỏi, chẳng hạn với câu a:
Đề bài cho biết gì, yêu cầu tính gì?
Độ dài từ nhà sâu vẽ bùa đến nhà sâu tơ bằng độ dài cạnh nào của hình chữ nhật ABCD?
(Bằng độ dài cạnh AD).
Làm thế nào để biết độ dài cạnh AD? (AD=BC)
Giải
a) Nhà sâu vẽ bùa cách nhà sâu tơ 12dm.
b) Nhà sâu vẽ bùa cách nhà sâu xám 20dm.
3.2.2. Dạng bài tập tính chu vi hình chữ nhật
Bài 5. Một quyển vở hình chữ nhật biết chiều dài 20cm, chiều rộng là 15cm. Tính chu vi quyển
vở hình chữ nhật.
Hướng dẫn: Công thức tính chu vi hình chữ nhật P = (a + b) x 2. Trong đó a là chiều dài 20cm,
b là chiều rộng 15cm. Vậy sẽ tính được chu vi của quyển vở.
Giải
Chu vi quyển vở hình chữ nhật là:
(20 + 15) x 2 = 70 (cm)
Đáp số: 70cm.
Bài 6 Một mảnh đất hình chữ nhật có chiều dài 35m, chiều rộng 20m. Tính chu vi mảnh đất đó.
Hướng dẫn: Công thức tính chu vi hình chữ nhật P = (a + b) x 2. Trong đó a là chiều dài 35m,
b là chiều rộng 20m. Vậy sẽ tính được chu vi của mảnh đất hình chữ nhật.
Giải
Chu vi mảnh đất hình chữ nhật là :
(35+20) × 2 = 110 (m)
Đáp số: 110m.
Bài 7. Chọn chu vi của hình