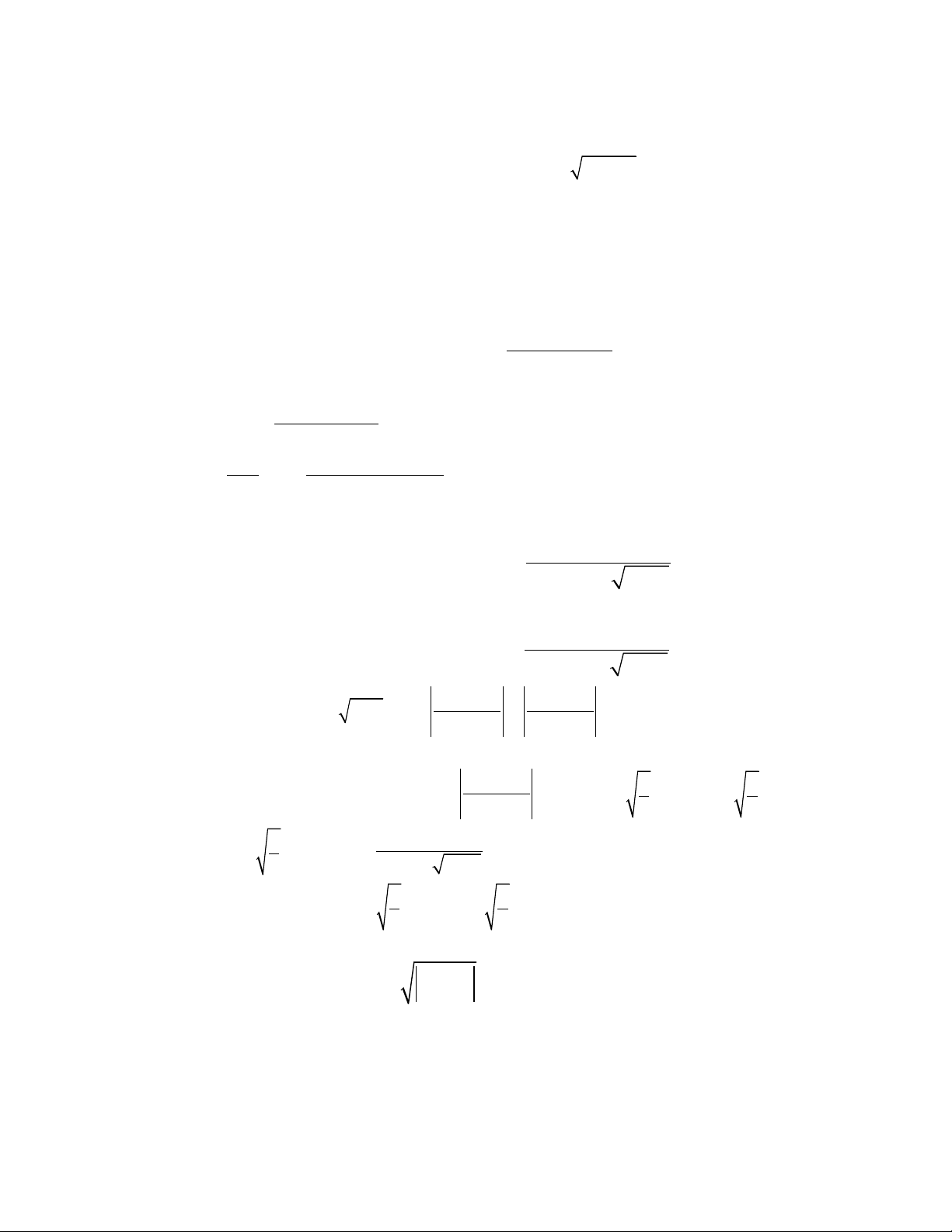
- 1 -
Đ 11:Ề
Câu 1: V kh i ẽ ố
Ω
gi i h n b i ớ ạ ở
2 2 2 2x y z y+ +
,
2 2
y x z +
.
Câu này các em t v .ự ẽ
Câu 2: Trên m t ph ng ặ ẳ
2 0x y z+ − =
tìm đi m sao cho t ng kho ng cách t đóể ổ ả ừ
đi m hai m t ph ng ể ặ ẳ
3 6 0x z+ − =
và
3 2 0y z+ − =
là nh nh t.ỏ ấ
Đi m c n tìm là giao đi m c a 3 m t ph ng trên và kho ng cách b ng không.ể ầ ể ủ ặ ẳ ả ằ
Tuy nhiên Th y nghĩ bài này không đúng, các em b qua.ầ ỏ
Câu 3: : Kh o sát s h i t c a chu i s ả ự ộ ụ ủ ỗ ố
3 3 3 2
1
(3 1)!
1 2 5n
n
n
=
−
� ��� �
Bài gi i:ả
Đ t ặ
3 3 3 2
(3 1)!
1 2 5
n
n
n
µ
−
=� ��� �
( ) ( )
( )
1
3
3 3 1 3 2
lim lim 9 1
1
n
n n
n
n n n
n
µ
µ
+
+ +
= = >
+
=> chu i phân kỳ theo tiêu chu nỗ ẩ
D'Alembert
Câu 4: Tìm mi n h i t c a chu i lũy th a ề ộ ụ ủ ỗ ừ
Bài gi i:ả
Tìm mi n h i t c a chu i lũy th a ề ộ ụ ủ ỗ ừ
=
1
n
n
µ
=
2 2
5( 2) 5( 2)
lim | | lim 3 3
nn
n n
x x
µ
+ +
= =
Đi u ki n c n đ chu i h i t ề ệ ầ ể ỗ ộ ụ
2
5( 2)
3
x+
<1
x=
3
25
−
=>
( 1)
(2 1) 2
n
n
n n
µ
−
=+ +
h i t tuy t đ iộ ụ ệ ố
v y mi n h i t :ậ ề ộ ụ
Câu 5: Tính tích phân kép
2
D
I y x dxdy= −
��
, trong đó D là mi n ph ng gi i ề ẳ ớ
h n b i ạ ở
1 1,0 2x y−
.
- 2 -
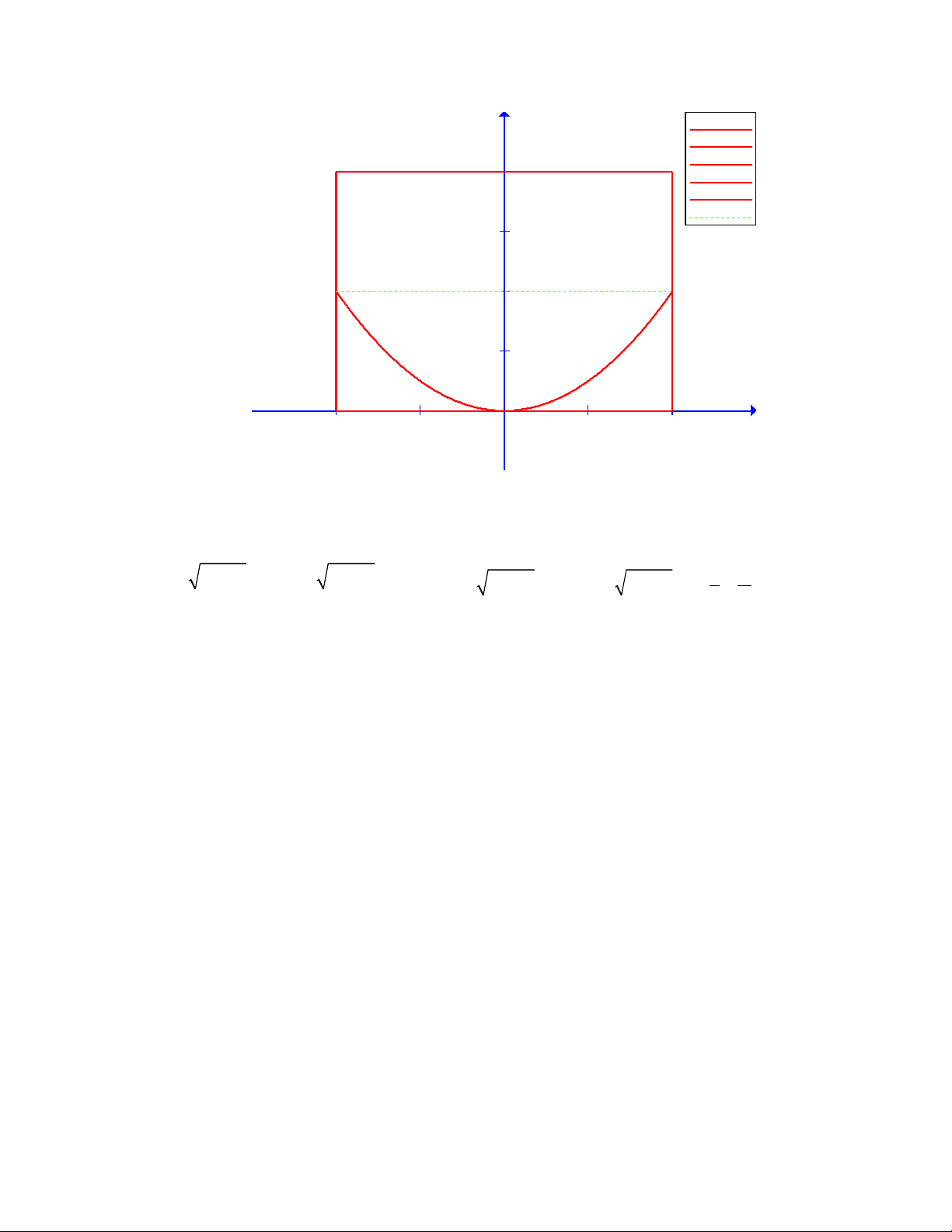
Bài gi i:ả
f(x)=0
f(x)=2
x(t)=-1 , y(t)=t
x(t)=1 , y(t)=t
f(x)=x^2
f(x)=1
-1 -0.5 0.5 1
0.5
1
1.5
2
x
y
Chia D thành 2 ph n:ầ
D1 là ph n ầ
2
y x
(phía trên Pparrabol)
D2 là ph n ầ
2
y x<
(phía d i Parabol)ướ
1 2
2 2
D D
I y x dxdy x ydxdy= − + −
�� ��
2
2
1 2 1
2 2
1 1 0
5
3 2
x
x
dx y x dy dx x ydy
π
− −
= − + − = +
�� ��
Ta có th làm gi m nh bài toán b ng cách nh n xét D đ i x ng qua oy và hàmể ả ẹ ằ ậ ố ứ
f(x,y) ch n theo bi n x nên I b ng 2 l n tích phân trên n a bên ph i c a mi n Dẵ ế ằ ầ ử ả ủ ề
r i làm t ng t .ồ ươ ự
Câu 6: Tính tích phân b i ba ộ
( )
V
I y z dxdydz= +
���
, trong đó V là v t th đ c gi iậ ể ượ ớ
h n b i ạ ở
2 2 2 2 2 2
, 4, 2z x y x y z x y= + + = = + +
.
Bài gi i:ả:
2 2
: 4D x y
+ =
Đ i sang to đ tr :ổ ạ ộ ụ
2 2
cos 0 2
sin 0 2
2
x r
y r V r
z z r z r
ϕ ϕ π
ϕ
=
� �
=�
� �
� �
= +
2
2
2 2 2
0 0
( sin ) 24
r
r
I d dr r r z dz
π
ϕ ϕ π
+
= + =�� � �
Câu 7:
Tính tích phân m t lo i hai ặ ạ
(2 )
S
I x y dydz= +
��
, v i S là ph n m t ớ ầ ặ
2 2
z x y= +
b c tị ắ
b i m t ở ặ
4z=
, phía trên theo h ng tr c Ozướ ụ
- 3 -
Bài gi i:ả
Cách 1:
{
2
4
2
2 2
:4
z
Oyz z y
y
Dy z
−
Chia S làm 2 ph n:ầ
S1: phía tr c mp(0yz) ướ
2
x z y= −
và pháp vecto t o v i ox góc tùạ ớ
S2: phía tr c mp(0yz) ướ
2
x z y= − −
và pháp vecto t o v i ox góc nh n.ạ ớ ọ
Do đó ta có:
()()
2 2
2 2
2 2
4 4
2 2
2 2
(2 )dyd ( 2 )dyd
2 2 16
D D
y y
I z y y z z y y z
dy z y y dz dy z y y dz
π
− −
= − − + + − − +
= − − + + − − + = −
�� ��
�� ��
Các em có th làm đ n gi n bài toán ngay t đ u b ng cách:ể ơ ả ừ ầ ằ
Nh n xét S đ i x ng qua oyz và hàm x(y,z)=y ch n theo x và x(y,z)=2x l theo xậ ố ứ ẵ ẻ
nên ta có:
1
0
2 2 2
S
S S
ydydz
xdydz xdydz
=
=
��
�� ��
v i Sớ1 là n a m t S phía tr c.ử ặ ướ
Khi đó:
2
2 2 dyd 16
D
I z y z
π
= − − = −
��
Cách 2: Dùng pháp véc t đ n v đ a v tích phân đ ng lo i 1ơ ơ ị ư ề ườ ạ
Cách 3: Thêm vào ph n m t z=4 r i dùng công th c O-Gầ ặ ồ ứ
Cách 2 và 3 nhanh và hay h n cách 1.. Các em t làm 2 cách sau nhé (d thôiơ ự ể
đ ng lo)ừ
- 4 -
Đ 12Ề
Câu 1: Tính
'(1,1)
x
f
c a hàm ủ
2 2
( , ) 2 4f x y x y= + − −
và bi u di n hình h c c aể ễ ọ ủ
đ o hàm riêng này nh là h s góc c a ti p tuy nạ ư ệ ố ủ ế ế
Bài gi i:ả
(1,1) 2 2
x
f= +
1
' (1,1) 2
x
f= −
M t ph ng y=1 c t ặ ẳ ắ
( , )f x y
t o thành đ th Cạ ồ ị 1
Ti p tuy n c a Cế ế ủ 1 t i đi m M(1,1,ạ ể
2 2+
) có h s góc là: ệ ố
1
' (1,1) 2
x
f= −
Câu 2: Tìm gtln, gtnn c a ủ
3 3
( , ) 3f x y x y xy= + −
trên mi n ề
0 2, 1 2x y −
Bài gi i:ả
2
' ( , ) 3 3
x
f x y x y= −
=0
2
' ( , ) 3 3
y
f x y y x= −
=0
x=y=1
khi x=0 =>
3
( ) , [ 1,2] ax 8, min 1f y y y m= − = = −� �
;
khi x=2 =>
3
( ) 6 8, [ 1,2] max 13,min 4f y y y y= − + − = =� �
khi y=-1 =>
3
( ) 1 3f x x x= − +
;
2
'( ) 3 3f x x= +
vô nghi mệ
khi y=2 =>
3
( ) 8 6 , (0,2)f x x x x= + −
;
2
'( ) 3 6f x x= −
=>
( )
2 2,2 8 4 2x f= = −�
Max f=13 đ t t i (2,-1), min f =-1 đ t t i (0,-1)ạ ạ ạ ạ
Câu 3: Kh o sát s h i t c a các chu i s : ả ự ộ ụ ủ ỗ ố
1
( 1)
1
n
n
nn
=
−
+
Bài gi i:ả
lim | | 1 0
n
nu
=
=> chu i phân kỳ theo đi u ki n c n.ỗ ề ệ ầ
Câu 4: Tìm bán kính h i t c a chu i lu th a ộ ụ ủ ỗ ỹ ừ
3 3
1
(2 1)( 3)
3 ln
n
n
n x
n n n
=
+ −
+
Bài gi i:ả
lim 3
nn
nu x
= −
Đ chu i h i t => ể ỗ ộ ụ
3 1x− <
=>
2 4x
< <
x=2 =>
1/2 3
3 3
( 1) (2 1) ( 1) 2
3 ln
3 .ln
n n
n
n
un n
n n n
− + −
=+;
h i t theo tiêu chu n Leibnitzộ ụ ẩ
- 5 -
x=4 =>
1/2 3
3 3
(2 1) 2
3 ln
3 .ln
n
n
un n
n n n
+
=+;
phân kỳ theo tiêu chu n tích phânẩ
v y ậ
2 4x <
Câu 5:Tính tích phân kép
{ }
max ,
D
I x y dxdy=��
trong đó D là mi n ph ng gi iề ẳ ớ
h n ạ
b i ở
0 4,0 4x y
.
Bài gi i:ả
Chia mi n D b i đ ng th ng y=x thành 2 mi n Dề ở ườ ẳ ề 1 và D2.
Trên D1(n m d i dt y=x) x>y nên max{x,y}=xằ ướ
Trên D2(n m trên dt y=x) x<y nên max{x,y}=yằ
1 2 1 2
256
3
D D D D
I xdxdy ydxdy= + = + =
�� �� �� ��
Câu 6: Tính tích phân b i ba ộ
V
I xdxdydz=���
, trong đó V là v t th đ c gi i h nậ ể ượ ớ ạ
b i ở
2 2 2 2 2
0, 2x y z x y z+ + + +
.
Bài gi i:ả
Đ i sang to đ tr ổ ạ ộ ụ
2 2
cos 0 2
sin 0 1
2
y r
z r V r
x x r z r
ϕ ϕ π
ϕ
=
=�
� �
� �
=
− − −
2
2
2 1
0 0 2
7
12
r
r
I d dr rxdx
π
π
ϕ
−
− −
= = −
� � �
Câu 7: Tính tích phân m t lo i hai ặ ạ
3 3 3
S
I x dydz y dxdz z dxdy= + +
��
v i S là m t phíaớ ặ
ngoài c a v t th gi i h n b i ủ ậ ể ớ ạ ở
2 2 2 ,0 1x z y y+
.
Bài gi i:ả
Áp d ng công th c O-G:ụ ứ
3 3 3 2 2 2
3 ( )
S V
I x dydz y dxdz z dxdy x y z dxdydz= + + = + +
�� ���
Đ i sang to đ tr : ổ ạ ộ ụ
cos 0 2
sin 0 1
1
z r
x r V r
y y r y
ϕ ϕ π
ϕ
=
� �
� �
=�
� �
� �
=
� �
2 1 1 2 1
2 2 2 3
0 0 0 0
4 1 9
3 ( ) 3 ( )
3 3 10
r
d rdr r y d y d r r rdr
π π
φ φ π
= + = − + =
� � � � �
Các em có th đ i sang to đ c u đ tính tích phân.ể ổ ạ ộ ầ ể